8751

80

T1 ×V γ −11 = T2 ×V γ −12 (const) .

Из этого равенства найдем:

Характер изменения давления при адиабатическом процессе также можно найти, исходя из (2.23), если заменить в нем температуру, воспользовавшись уравнением Клайперона - Менделеева (T=pVµ/mR). В результате получим:

T ×V γ −1 = pV γ × μ / mR = const .

Поскольку m, µ, R являются постоянными для данной массы газа,

Это соотношение называется уравнением адиабаты Пуассона.

Работа при адиабатическом расширении газа равна площади под кривой процесса 1-2 (см. рис.2.2). Если известны начальная и конечная температуры процесса, то нет необходимости вычислять эту площадь - достаточно воспользоваться формулой (2.18) и выражением для внутренней энергии идеального газа. Это приведет нас к соотношению:

2.3. Второе начало термодинамики

Первое начало термодинамики устанавливает неизменность общего количества энергии в изолированной термодинамической системе и эквивалентность разных видов энергии при их превращениях в

1.Невозможен процесс, единственным конечным результатом которого является передача энергии в форме теплоты от холодного тела к горячему (формулировка Р.Клаузиуса).

2.Невозможен процесс, единственным результатом которого является отнятие от некоторого тела энергии в форме теплоты и превращение этой энергии в эквивалентную ей работу (формулировка В.Томсона).

Обе формулировки эквивалентны. Действительно, пусть существует процесс, с помощью которого можно было бы повысить температуру одного

81

тела за счет охлаждения другого, при одинаковых начальных температурах обоих тел. Тогда, используя известные процессы, можно было бы превратить полученную разность температур в механическую энергию без каких-либо изменений в состоянии окружающей среды.

Таким образом, если бы могли происходить процессы, запрещенные вторым началом термодинамики, то за счет отбора энергии в форме теплоты, например от мирового океана, имелся бы практически неисчерпаемый источник механической энергии. Подобное устройство было бы равноценно вечному двигателю. Поэтому второе начало термодинамики иногда

формулируют так: <<Невозможен вечный двигатель второго рода>>.

2.3.1. Термодинамические циклы. Цикл Карно

Циклом, как указывалось ранее, называется такой процесс, в результате которого термодинамическая система возвращается в исходное состояние. Циклы или круговые процессы используются во всех тепловых машинах: двигателях внутреннего сгорания, газотурбинных установках, холодильниках и т.п. Изучение циклов является одной из основных задач термодинамики.

b

V

C D

Рис. 2.5. Схема прямого цикла тепловой машины

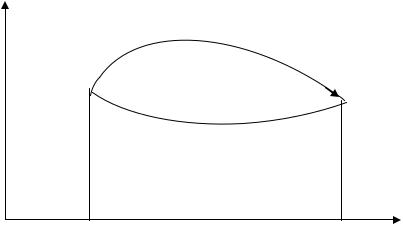
Рассмотрим произвольный цикл 1-а-2-b-1, изображенный на рис. 2.5. Его можно разбить на два процесса: 1-а-2 - процесс расширения и 2-b-1 - процесс сжатия. На участке 1-а-2 газ получает извне количество теплоты Q1 и в результате совершается работа и изменяется внутренняя энергия газа:

Q1=A1+(U2-U1). (*)

Работа A1 может быть найдена как площадь фигуры С1a2D.

На участке 2-б-1, наоборот, внешние силы совершают положительную работу A2 над газом, а работа газа – A 2 при этом отрицательна. Для того, чтобы суммарная работа газа AΣ, численно равная площади фигуры, ограниченной кривой 1a2b1, при выбранном направлении цикла была положительна (AΣ=A1- A2>0), процесс сжатия должен происходить при меньшем давлении и температуре. Это означает, что в ходе процесса сжатия газ необходимо охлаждать, отводя от него тепло другому телу. Другими словами количество

82

теплоты, полученное газом при сжатии –Q 2 - величина отрицательная (Q2>0 - теплота, отданная газом). Таким образом, уравнение первого начала термодинамики для процесса 2-b-1 можно записать в виде:

-Q2=(U1-U2)-A2/ (**)

Из равенств (*) и (**) нетрудно получить

AΣ=A1-A2=Q1-Q2.

Это равенство выражает первое начало термодинамики для полного цикла.

Оно показывает, во-первых, что работа совершается вследствие превышения теплоты Q1, полученной газом при расширении, над теплотой Q, отданной им при сжатии. Во-вторых, можно сделать вывод, что при циклическом процессе невозможно все полученное от нагревателя тепло превратить в работу - необходимо <<поделиться>> частью полученного тепла с другим телом,

которое является холодильником.

КПД тепловой машины. Цикл с положительной работой газа называется прямым циклом и лежит в основе всех тепловых двигателей. В них рабочее вещество (газ или пар) получает от нагревателя некоторую теплоту, а отдает холодильнику теплоту Q2. Отношение

показывает, какая доля полученной от нагревателя теплоты превращена в работу и носит название коэффициента полезного действия тепловой машины. Видим, что эта величина не может быть большей 1.

КПД холодильной машины. Если при круговом процессе газ, расширяясь, совершает работу, меньшую той работы, которую производят внешние силы при его сжатии, т.е. A1<A2, то такой цикл носит название обратного цикла. Он может происходить, когда расширение газа происходит при более низкой температуре, чем сжатие. Легко видеть, что обход прямого цикла на графике в координатах {p,V} всегда происходит по часовой стрелке, а обратного цикла - против часовой стрелки.

Обратные циклы используются в холодильных установках. В холодильных установках рабочее тело отбирает тепло Q2 у тела с более низкой температурой, вызывая его охлаждение, и отдает телу с более высокой температурой теплоту Q1 (по аналогии с прямым циклом Q2<Q1). Этот процесс требует совершения работы внешними силами, AΣ=A2 – A 1. Первое начало термодинамики для обратного цикла запишется в виде:

Q2-Q1=A1-A2<0.

Поскольку цель холодильника - забрать тепло от охлаждаемого тела, а затраты при этом - совершаемая работа, эффективность холодильника можно характеризовать отношением Q2 к AΣ. Это отношение:

может превышать 1 и называется холодильным коэффициентом.

83

Эффективность теплового насоса. Обратный цикл может использоваться также для обогрева. При этом теплота Q2 забирается из внешней среды и в обогреваемое помещение (при более высокой температуре) передается теплота Q1. Обогрев производится за счет внешней силы и все соотношения между величинами в точности совпадают с величинами для холодильника. Однако, поскольку цель в данном случае другая - обогреть помещение, то <<польза>> определяется количеством теплоты, переданным помещению т.е. величиной Q1, а затраты - по-прежнему состоят в совершении работы AΣ. Такое устройство называется тепловым насосом, а его эффективность определяется формулой:

Q1

1

и всегда превышает единицу. В связи с этим заметим, что старый анекдот о том, что некоторые народности Крайнего Севера греются в холодильниках, имеет под собой научную основу! Правда бытовой холодильник в этом случае следует разместить камерой на улицу (с открытой дверцей), а теплообменником (задняя часть холодильника) - внутрь помещения.

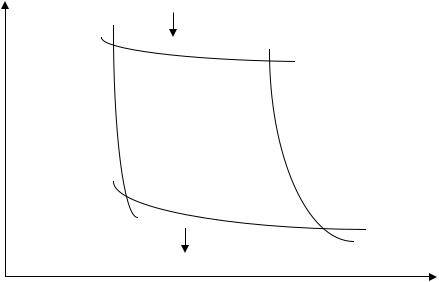
Цикл Карно. В термодинамике особое место занимает цикл, рассмотренный французским инженером Сади Карно в 1824 году. Цикл состоит из четырех обратимых процессов для идеального газа (см. рис. 2.3.1). Подразумевается, что имеется нагреватель с температурой T1 и холодильник с температурой T2.

цикла максимальный по сравнению со всеми другими возможными рабочими

84

циклами в диапазоне температур между Т1 и Т2, а также не зависит от рода рабочего тела. Действительно, на участке 1-2 тело получает от нагревателя теплоту, которая вся (без потерь) идет на выполнение работы (см. 2.17) A1-2:

Значения объема V1 газа в точке 1 и V2 в момент окончания изотермического участка 1-2, как будет видно, не войдут в окончательное выражение для КПД.

Далее газ необходимо подготовить к стадии сжатия. Чтобы работа газа в цикле была положительной, необходимо понизить давление, охладив газ от температуры T1 до T2. Охлаждение осуществляется на участке 2-3 адиабатически. Этот процесс также оптимален, поскольку на этом участке не происходит потери тепловой энергии (δQ=0), а, кроме того, совершается дополнительная положительная работа A2-3 за счет уменьшения внутренней энергии газа (см. выражение 2.25)):

A2−3 = mμ Cυ × (T1 - T2 ) .

Таким образом, на стадии расширения газ совершил работу A1=A1-2+A2-3, получив теплоту Q1.

В процессе 3-4 изотермического сжатия газа от объема V3, который газ имел в конце адиабатического расширения, до некоторого объема V4 газ совершает работу A3-4, получив такое же по величине количество тепла Q3-4:

Поскольку V4<V3, логарифм в этой формуле, а вместе с ним и величины Q3- 4=A3-4 отрицательны, что означает не получение газом, а передачу тепла Q2=- Q3-4 холодильнику. Положительная работа также совершается внешними силами. Работа внешних сил на этом участке имеет наименьшее из возможных значение, поскольку газ все время имеет наименьшую температуру T2 (значит, и наименьшее давление).

Участок 4-1 необходим, чтобы вернуть газ в исходное состояние с температурой T1. Это нагревание в цикле Карно осуществляется также оптимальным образом - адиабатически (без затраты тепловой энергии). При этом работа A4--1<0, т.е. совершается над газом внешними силами.

Нетрудно убедиться, что A2-3=-A4-1 и работа газа на двух адиабатических участках компенсирует друг друга, так же как и изменение внутренней энергии (теплопередача на этих участках отсутствует). Поэтому основу цикла составляют два изотермических процесса, при первом из которых полученная теплота полностью превращается в работу, а второй происходит при наименьшей возможной температуре и давлении и соответствует наименьшей отрицательной работе газа и наименьшей теплоотдаче холодильнику. Эти доводы еще раз подчеркивают оптимальность цикла Карно.

Подставив величины Q1 и Q2 в общую формулу (2.26), вычислим КПД идеальной тепловой машины Карно:

85

η = T1 ln(V2 /V1 ) − T2 ln(V3 /V4 ) .

T1 ln(V2 /V1 )

Найдем соотношения между объемами V1, V2, V3, V4. Напишем соотношение для адиабатного расширения газа от объема V2 до V3 и для адиабатического сжатия от объема V4 до V1 (см. формулу 2.21):

T1V2γ-1=T2V3γ-1,

T1V2γ-1=T2V4γ-1,

Поделим левую часть первого равенства на левую часть второго, а правую часть первого на правую часть второго (если делить два равных числа на равные числа, равенство сохранится):

Это равенство можно упростить:

V2 = V3

V1 V4

и с его помощью исключить V2/V1 в выражении для η. Это приведет к сокращению одинаковых логарифмических множителей. Окончательно получим:

Этот вывод можно сформулировать так: термический КПД цикла Карно не

зависит от природы рабочего тела и является только функцией температур нагревателя и холодильника. Это заключение получило название теоремы

Карно.

Цикл Карно сыграл большую роль в развитии тепловых двигателей.

Т2 тот цикл будет иметь больший КПД, который ближе к циклу Карно.

2.3.2. Понятие об энтропии

Помимо внутренней энергии в термодинамике большую роль играет еще одна функция состояния, которая получила название энтропия.

Величина Q/T называется приведенной теплотой. Приведенная

теплота, полученная телом, равна количеству полученной теплоты, деленной на температуру тела. Уже говорилось, что подведенная к системе теплота при переходе от одного состояния в другое зависит от пути процесса, а при совершении цикла не равна нулю. С точки зрения математики это означает, что теплота не является полным дифференциалом.

В случае цикла Карно тело получает теплоту Q1 при изотермическом расширении с температурой T1 и отдает тепловую энергию Q2 при температуре

86

T. Полная теплота, полученная телом за цикл Q1-Q2, не равна нулю. В то же время приведенное количество теплоты, полученное телом при расширении, равно Q1/T1, а при сжатии –Q 2/T1 (теплообмен газа с внешними телами осуществляется только на изотермах). Оказывается, количество приведенной теплоты, полученной газом за цикл, равно нулю4:

что означает также независимость приведенного количества теплоты от пути процесса, а только от начального и конечного состояний, т.е. является функцией состояния. Математическим языком о том же самом можно сказать, что приведенное количество теплоты является полным дифференциалом

некоторой функции состояния S. Функция состояния S называется энтропией. Из определения (2.30) следует, что если у системы в начальном состоянии

{р1,V1,Т1} была энтропия S1, то при переходе в другое состояние при равновесном процессе ее энтропия будет равна:

Пример

Определить изменение энтропии 200г воды, охлаждаемой от t1=18˚C до t2=0˚C.

Рассмотрим некоторые свойства энтропии, следующие из определения.

∙Энтропия нескольких тел равна сумме энтропий этих тел:

S= ∑iN=1 Si .

∙При равновесных процессах без передачи тепла (адиабатических процессах) энтропия системы не меняется.

S=const, если Q=0.

∙Энтропия, как и все функции состояния, определяется с точностью до константы, поэтому измеримой величиной является только разность энтропий в начальном и конечном состояниях.

4 Для доказательства используем общее выражение для КПД тепловой машины, приравняв, его КПД цикла Карно:

87

∙При постоянном объеме энтропия является функцией внутренней

энергии тела. Действительно, согласно первому началу термодинамики: если dV=0, то δQ=dU, следовательно

dS = dU . T

Выразим значения энтропии идеального газа через термодинамические параметры, воспользовавшись уравнениями состояния, выражением для внутренней энергии и первым началом термодинамики:

процессев идеальном газе. Используя уравнение состояния идеального газа и уравнение Майера (Cр-Cυ=R), можно выразить энтропию газа через давление p, что в некоторых случаях более удобно:

S = mμ (C p ln T + R ln p)+ const .

Энтропия изолированной системы. Энтропия изолированной системы

при обратимых процессах остается постоянной.

Действительно, тепловая машина с нагревателем и холодильником (в частности, машина Карно) составляет изолированную систему. Энтропия системы равна сумме энтропий нагревателя Sн, газа Sг и холодильника Sx. Если передача тепла от нагревателя газу происходит при одинаковой температуре газа и нагревателя T1, то процесс теплопередачи является обратимым. То же самое справедливо для передачи тепла от газа холодильнику, имеющему температуру T2. В процессе передачи тепла Q1 газу имеем:

и температура системы не меняется. Аналогичные рассуждения приводят к выводу об отсутствии изменения энтропии системы при передаче теплоты Q2 от газа холодильнику при температуре T2.

Рассмотрим теперь необратимый процесс теплопередачи в изолированной системе. Пусть два равных количества идеального газа с температурами T1 и T2 (T1<T2), содержатся в изолированных одинаковых сосудах с жесткими стенками. Если создать тепловой контакт между этими сосудами, то через некоторое время газы в сосудах придут в термодинамическое равновесие, их температуры сравняются и будут равны T=(T1+T2)/2 (из равенства количества теплоты, получаемого первым газом и отдаваемого вторым газом: Cгаза (T-

T1)=Cгаза(T2-T)). Согласно (2.32), энтропия первого газа (объем газа не меняется) возрастет на:

89

пересчитывать различные данные, которыми принято описывать влажность воздуха.

3.1. Реальные газы. Уравнение Ван-Дер-Ваальса

Как отмечалось ранее, кинетическая теория идеального газа не учитывает сил взаимодействия молекул, сами же молекулы принимаются за точки. Такая модель соответствует достаточно разреженному газу, подчиняющемуся законам Бойля -Мариотта и Гей-Люссака.

Многочисленные опыты показали, что все газовые законы и, в частности, формула Клайперона - Менделеева носят приближенный характер. Чем сильнее сжат газ, тем заметнее его отклонение от газовых законов. Для того, чтобы можно было применить формулу Клайперона - Менделеева к реальным газам, очевидно, необходимо ввести в нее какие-то поправки. Одно из наиболее удачных уточнений этой формулы предложил в 1983 г. голландский физик Ван- дер-Ваальс.

Первое уточнение Ван-Дер-Ваальса касается объема самих молекул. В 1см3 газа при нормальных условиях содержится 2,7 1019 молекул. Принимая эффективный диаметр молекулы равным 3·10-8см, определяем, что ее объем равен 1,2·10-23см3. Находим, что объем всех молекул, находяхщихся в 1см3 газа при нормальных условиях, составляет около 3·10-4см3. Однако при давлении 2500 атм объем самих молекул уже составит половину всего объема газа. Поэтому при высоких давлениях объем газа, занимаемый самими молекулами, необходимо учитывать.

Так как при сжатии газа уменьшается обратно пропорционально давлению не весь объем, а объем свободного пространства между молекулами, в формуле Клайперона - Менделеева вместо V следует ввести (V-b), где b – объем несжимаемой части газа. По вычислению Ван-Дер-Ваальса, b приблизительно равно учетверенному объему всех молекул. Поясним, как получается такой результат.

Действительно, центры молекул не смогут сблизиться больше, чем на расстояние, равное удвоенному эффективному радиусу (2r), т.е. проникнуть в пространство, соответствующее объему шара радиуса 2r (см. рис. 3.1). Объем

соответствует объем несжимаемого пространства, равный учетверенному объему одной молекулы (4V0).

Второе уточнение, введенное Ван-Дер-Ваальсом, касается давления газа. При разреженном состоянии газа силы сцепления между его молекулами ничтожно малы. Однако при сжатии газа промежутки между молекулами уменьшаются и силы их взаимодействия возрастают. Эти силы притяжения молекул друг к другу как бы помогают силам внешнего давления сжимать газ. Следовательно, в формулу Клайперона - Менделеева вместо внешнего давления