8507

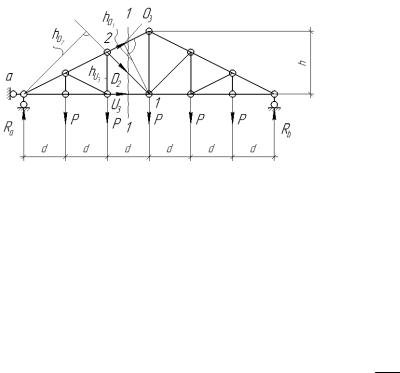
Отбросив одну из отсеченных частей фермы (удобнее отбросить ту часть фермы, где больше сил), заменяют действие отброшенной части фермы действием неизвестных усилий, направленных вдоль рассеченных стержней. При этом, неизвестные усилия всегда предполагаются растягивающими. Для отсеченной части фермы составляют три уравнения равновесия статики в одной из трёх возможных разновидностей:

решая которые определяют неизвестные усилия.

Следует стремиться вести вычисления так, чтобы усилие в каждом стержне определялось независимо от усилий в других стержнях, что избавляет от нарастания погрешностей и увеличивает точность расчета.

Способ моментных точек.

Этот способ применяют в тех случаях, когда можно провести сечение через три стержня, направления которых не пересекаются в одной точке.

Пусть для фермы по рисунку требуется определить усилия О3 , D2 , U3 . Считаем опорные реакции найденными. Проведем сечение 1-1 через изучаемые стержни. Отбросим правую часть фермы и заменим ее действие неизвестными усилиями, полагая их растягивающими.

Для определения усилия O3 составим уравнение равновесия, в виде суммы моментов сил, приложенных к левой отсеченной части фермы, относительно точки “1” – точки пересечения направлений усилий D2 и U3 :

В этом выражении числитель представляет собой момент M10 левых внешних сил относительно точки 1 (изгибающий момент в сечении воображаемой балки – балочный

момент). Таким образом, можно записать: O3 M10 , где M10 - момент левых внешних hO3

31

Для определения усилия D2 выбираем моментную точку A – точку пересечения

Таким образом, при применении способа моментных точек усилие всегда выражается отношением момента внешних сил, действующих на отсеченную часть фермы, относительно моментной точки, к плечу изучаемого усилия относительно этой же точки.

Этот способ может быть применен и в том случае, когда сечение рассекает более трех стержней при условии, что все стержни, кроме изучаемого, пересекаются в одной точке.

опорной реакции рассматриваемой отсеченной части фермы относительно т. 1.

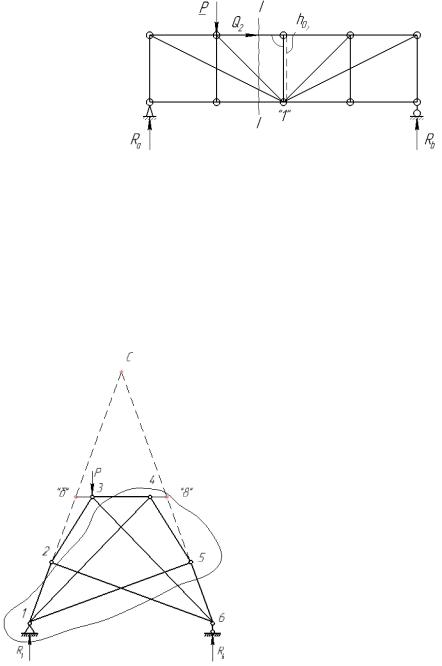
Для определения усилий в стержнях ряда ферм бывает целесообразно использовать замкнутое сечение. С помощью замкнутого сечения выделяется часть фермы с тремя неизвестными усилиями в рассеченных стержнях, которые определяются из уравнений равновесия, составленных для этой рассматриваемой части.

На рисунке изображена статически определимая и геометрически неизменяемая ферма. Проведем замкнутое сечение и рассмотрим равновесие внутренней части фермы. Стержни 2-6 и 3-6 пересеченные дважды, будут уравновешены усилиями, приложенными по их концам и в уравнения равновесия статики не войдут.

Выбирая для определения неизвестных усилий в стержнях 1-2, 3-4 и 5-6 соответствующие моментные точки (для каждого из определяемого усилия моментная точка выбирается на пересечении усилий двух других стержней), составляем независимые уравнения равновесия и определяем искомые усилия.

Частным случаем способа моментных точек является способ проекций, когда два из пересекаемых сечением стержня параллельны друг другу, т.е. моментная точка нахо-

32

дится в бесконечности. В этом случае для определения усилия в одном из стержней составляется уравнение равновесия в виде суммы проекций всех сил, приложенных к отсеченной части, на ось, перпендикулярную к направлениям параллельных стержней.

8.2.3. Способ совместных сечений

Если в ферме невозможно провести сечение через три стержня, а только через большее количество стержней, то и неизвестных усилий будет больше уравнений равновесия статики. Следовательно, для таких ферм определение усилий с помощью одного сечения становится невозможным.

Способ совместных сечений целесообразно применять в тех случаях, когда удается провести два разреза таким образом, чтобы каждый из них пересекал четыре стержня, причем какие-либо два повторялись в обоих разрезах.

Способ совместных (например, двух) сечений заключается в решении задачи при помощи составления совместной системы двух уравнений с двумя неизвестными. Так например, рассмотрим ферму, изображенную на рисунке.

Проведя сечения 1-1 и 2-2, запишем уравнения моментов для отсеченной части, лежащей выше сечения 1-1 и той части, которая лежит ниже сечения 2-2. Первое уравнение составим относительно моментной точки O, а второе – относительно точки O1. Будем иметь:

1.MO 0: D3 6 h3 6 D4 1 h4 1 MO 0

2.MO1 0: D1 4 h1 4 D6 3 h6 3 MO1 0

где: MO и MO1 моменты внешних сил относительно моментных точек O и O1 соответственно для верхней и нижней отсеченных частей фермы.

Оба уравнения содержат одни и те же неизвестные усилия в пересеченных диагональных стержнях. Решая систему уравнений, определяем неизвестные усилия.

8.3. Частные случаи равновесия узлов ферм. Нулевые стержни.

При расчете ферм встречаются случаи, когда в некоторых стержнях при заданной нагрузке не возникает усилий. Такие стержни будем называть нулевые. Наличие нулевых стержней дает возможность существенно упростить решение задач при определении усилий в фермах. Рассмотрим некоторые характерные случаи.

а) Двухстержневые узлы.

В ненагруженном двух стержневом узле оба стержня являются нулевыми. В самом деле, если в этих стержнях возникнут усилия, то равнодействующая этих усилий ничем не уравновесится, следовательно и узел не сможет находиться в равновесии.

33

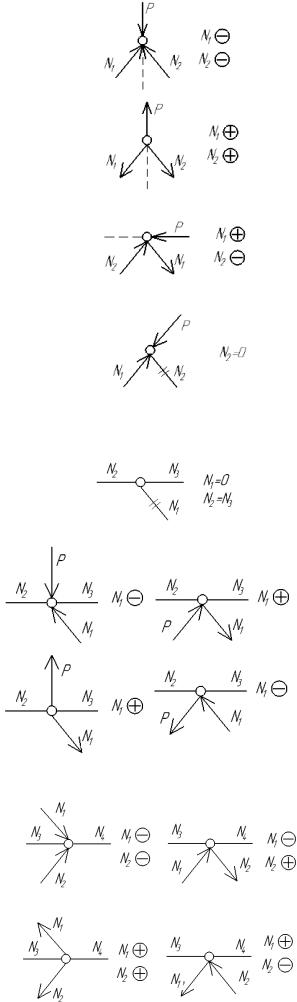
Нагруженные двухстержневые узлы:

-если линия действия нагрузки проходит внутри узла, образованного стержнями, то знаки усилий в них одинаковы (или оба сжаты при нагрузке, действующей в узел, или оба растянуты – при нагрузке, действующей от узла);

-если линия действия нагрузки проходит вне узла, образованного двумя стержнями, то знаки усилий в них разные – ближайший к силе стержень растянут, другой сжат;

-если линия действия узловой нагрузки совпадает с осью одного из стержней, то примыкающий стержень не работает, а другой стержень может быть сжат или растянут в зависимости от направления действия узловой нагрузки.

б) Трехстержневые узлы

- если в ненагруженном трех стержневом узле два стержня лежат на одной прямой, то усилие в примыкающем стержне равно нулю. Знаки усилий в стержнях, лежащих на одной прямой

всегда однозначны (оба растянуты или сжаты).

- если в нагруженном трех стержневом узле два стержня лежат на одной прямой, а примыкающий стержень и внешняя узловая нагрузка расположены по разные стороны от них, то знак усилия в примыкающем стержне всегда солидарен со знаком узловой нагрузки.

Если внешняя узловая нагрузка и примыкающий стержень расположены с одной стороны от стержней, лежащих на одной прямой, то знак усилия в примыкающем стержне противоположен знаку внешней узловой нагрузки;

в) Четырехстержневые узлы

- если в ненагруженном четырех стержневом узле два стержня лежат на одной прямой, а два примыкающих стержня расположены по разные стороны от них, то знаки усилий в примыкающих стержнях всегда однозначны. Если примыкающие стержни расположены с одной стороны от двух стержней, лежащих на одной прямой, то знаки усилий в примыкаю-

34

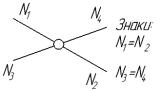
щих стержнях всегда разнозначны;

- в ненагруженном четырех стержневом узле усилия в стержнях, попарно лежащих на одной прямой, равны по величине и по знаку.

Задания для самостоятельной работы.

Литература: [1, гл. 1]; [4, гл. 1]; [2, гл. 1], [3, гл. 4].

Вопросы для самопроверки

1.Что называется фермой?

2.Какова действительная схема фермы?

3.В каких случаях жесткие узлы фермы могут быть заменены шарнирными узлами?

4.Какие внутренние усилия возникают в стержнях фермы?

5.Классификация ферм по назначению.

6.Какие фермы называются распорными?

7.Какая решетка называется раскосной?

8.Какая решетка называется полураскосной?

9.Какая решетка фермы называется треугольной?

10.По какой формуле определяется число степеней свободы фермы?

11.Как выполнить кинематический анализ фермы?

12.Как проводится структурный анализ решетки фермы?

13.Плоские статически определимые фермы. Классификация ферм, достоинства и недостатки в сравнении друг с другом.

14.Укажите признаки нулевых стержней.

15.Каковы преимущества и недостатки фермы по сравнению с балкой и аркой?

16.Методы определения усилий в стержнях статически определимых ферм. Способ вырезания узлов.

17.Способ моментных точек (простых сечений) для определения усилий в стержнях статически определимых ферм.

18.Способы совместных и замкнутых сечений для определения усилий в стержнях статически определимых ферм.

19.Частные случаи равновесия узлов ферм (леммы).

9. Теория перемещений статически определимых систем

9.1. Понятие о перемещении. Работа внешних сил.

Перемещения, вызванные деформацией элементов конструкции, определяют для проверки жесткости и устойчивости, а также для расчета статически неопределимых конструкций. Именно используя дополнительные уравнения деформаций, выражающих соотношения между перемещениями и внешними силами, определяют усилия в “лишних” связях статически неопределимых систем. В этой связи, теория определения перемещений стержневых систем имеет очень большое значение.

В основу определения перемещений в сооружениях положен принцип возможных перемещений для деформируемой системы.

Перемещением данной точки сооружения называется изменение ее координаты, вызванное деформацией сооружения. Мы будем определять перемещения в линейнодеформируемых системах, подчиняющихся закону Гука и принципу наложения, согласно

35

которому результат действия системы сил равен сумме результатов действия отдельных сил.

Будем различать действительные и возможные (виртуальные) перемещения для силы P .

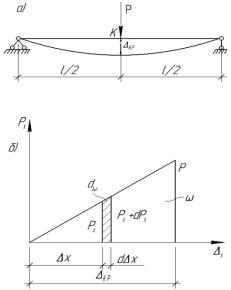
Действительным перемещением точки k kp

называют перемещение, вызванное силой P,

приложенной в точке k (рис. 9.1а). Оно, со-

гласно закону Гука, прямо пропорционально силе, т.е. kp kP P, где kP - перемещение

точки k при приложении единичной силы P в

этой точке в направлении изучаемого перемещения.

Рассмотрим статическое приложение силы, меняющейся от нуля до окончательного значения P (рис. 9.1б).

Промежуточное значение силы обозначим Px

, а соответствующее ему перемещение x .

При изменении силы на dPx , получим приращение в прогибе d x и элементарную работу внешних сил dApD Px d x .

Когда сила достигла конечного значения P, а перемещение стало равно kP , то действительная работа силы будет определяться интегралом

Для конкретности представления возможных перемещений, рассмотрим процесс приложения двух систем сил в последовательные интервалы времени (рис. 9.2а). Пусть на сооружение в первой стадии действует сила, приложенная статически и меняющаяся от нуля до конечного значения P. При этом вертикальное перемещение точки приложения силы P, которое обозначим PP , является действительным перемещением. Положим, что после действия силы P на сооружение в указанном деформированном состоянии действует

36

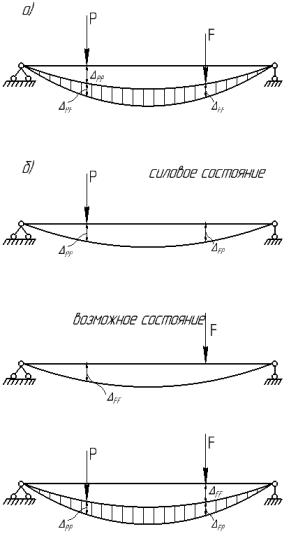
также статически новая сила F, которая вызывает дополнительные перемещения точек оси балки (заштрихованы на рис. 9.2а). При этом точка приложения силы P получает добавоч-

ное перемещение PF , величина которого соответствует окончательному значению силы

F. Так как первоначальные перемещения, вызванные силой P, считаем малыми, то добавочные перемещения, вызванные силой F, можно определить от недеформированного состояния и поэтому их можно считать независимыми от силы P.

Перемещение обозначаем PF : первый индекс

“p” обозначает точку приложения перемещения, соответствующего силе P, второй индекс “F” указывает на причину, вызывающую дан-

ное перемещение (сила F). Перемещение PF ,

вызванное в той же системе иной силой F, будет возможным перемещением для силы P. Рассмотрим теперь понятие о возможной работе силы P. Возможной работой силы будем называть работу этой силы на малом возможном перемещении точки приложения силы по ее направлению; для силы P (рис. 9.2а) возможной будет работа силы P на возможном перемещении PF .Так как перемещение PF

не зависит от силы P, то работа силы P выразится произведением силы P на перемещениеPF , т.е. APk P PF . Так как PF не зависит от силы P, то состояние действия силы F можно представить отдельно от состояния действия силы P. На рис. 9.2б показаны два независимых состояния одной и той же балки. Первое состояние – силовое состояние действия данной нагрузки P и второе состояние – возможное состояние действия силы F , на ко-

тором отмечено возможное перемещение PF . Пользуясь этими состояниями, можно оп-

ределить возможную работу силы F второго состояния на перемещении по направлению

Если изменить порядок приложения сил, а именно сначала приложить силу F, а затем силу P, то получим следующее выражение для полной работы:

37

не меняется. Приравняв эти два выражения, получим: P PF F FP .

Равенство формулирует теорему о взаимности возможных работ внешних сил:

возможная работа внешних сил первого состояния на перемещениях, вызванных силами второго состояния, равна возможной работе внешних сил второго состояния на перемещениях, вызванных силами первого состояния (теорема Бетти).

9.2.Работа внутренних сил. Потенциальная энергия деформации системы

Всооружении при его нагружении внешними силами за счет деформаций будет происходить накопление внутренней энергии, которая называется потенциальная энергия деформации системы (V).

Вусловиях идеальной упругости согласно законам сохранения механической энергии, работа внешних сил будет полностью переходить в потенциальную энергию деформации, т.е. A = V. Процесс накопления потенциальной энергии происходит за счет работы сил взаимодействия между частицами материала конструкции. В процессе нагружения внешние силы будут совершать положительную работу, величина которой определяется по теореме Клапейрона, а внутренние силы - отрицательную работу (при разгрузке – наоборот).

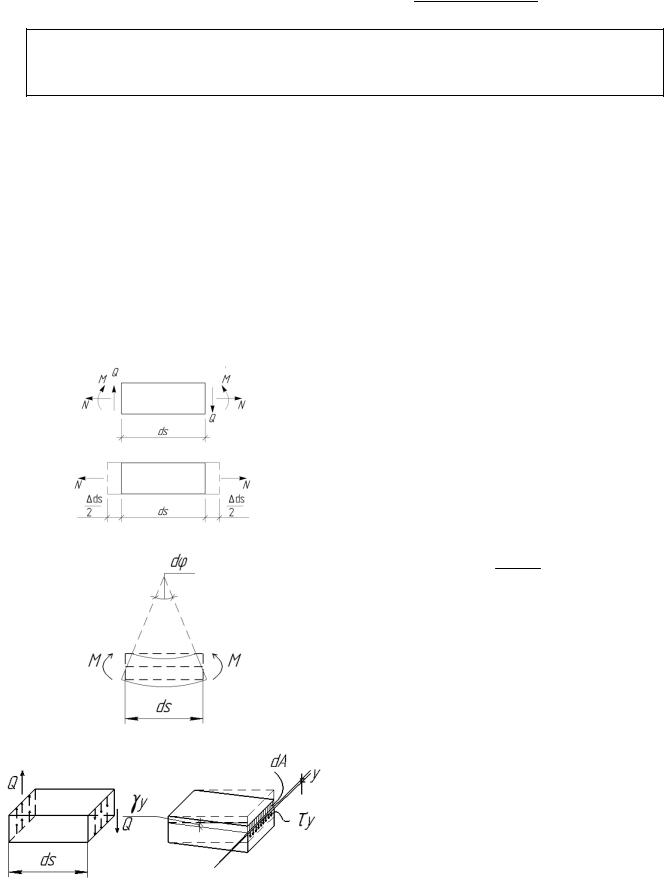
Выразим потенциальную энергию деформации в зависимости от возникающих в сечениях внутренних сил. Для этого рассмотрим бесконечно малый элемент под действием усилий M, Q и N , по отношению к которому их можно считать внешними силами.

При действии продольной силы N элемент ds

удлинится на величину ds. По закону Гука

ds N ds , E A

где E – модуль упругости, A – площадь, (E.A)

– жесткость стержня при растяжении (сжатии). Действительная работа внутренних сил N за счет деформации малого элемента ds будет

При действии изгибающего момента элемент ds изогнется (см. рисунок). Нейтральная ось искривится, но длина ее не изменится. Взаимный угол поворота соседних сечений также выражается в соответствии с законом Гука:

38

d M ds , где I – момент инерции сече-

E I

ния, (E.I) – жесткость стержня при изгибе. Действительная работа внутренних сил за счет изгиба от действия момента M бу-

При действии поперечной силы Q касательные напряжения распределены по высоте сечения неравномерно, а следовательно, и сдвиги разных волокон по высоте сечения различны. На площадке dA, расположенной на расстоянии y от нейтральной оси z, возни-

кает касательная сила, равная y dA. По закону Гука угол сдвига волокна будет равен

y , где G – модуль сдвига, а взаимное смещение двух торцов волокна будет равно:

G

Для определения работы силы Q необходимо просуммировать работы всех элементарных сил по площади A поперечного сечения. Тогда работа внутренних сил за

выражение y в формулу (а) и вынося за знак интеграла постоянные величины, получим:

сечения и поэтому для разных типов поперечных сечений определяется отдельно. Так,

например, для прямоугольного сечения = 1,2 , для круга = 1,185, для поперечного

A

Для того, чтобы получить действительную работу для одного стержня, необходимо проинтегрировать предыдущее выражение по длине этого стержня. Для стержневой системы в целом кроме этого необходимо выполнить суммирование значений действитель-

39

ной работы для всех ее элементов. Таким образом, окончательно действительная работа внутренних сил запишется в виде:

За счет потенциальной энергии при снятии нагрузки и происходит восстановление размеров и формы разгружаемой системы. При полном снятии нагрузки потенциальная энергия обратится в ноль. Из формулы видно, что потенциальная энергия всегда положительна.

Рассуждая аналогично, запишем выражение возможной (виртуальной) работы внутренних сил:

9.3. Теорема о взаимности удельных перемещений (теорема Максвелла)

Теорема о взаимности перемещений может быть получена как частный случай теоремы о взаимности работ (см. п. 9.1).

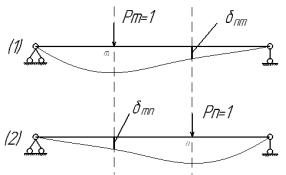
Применим теорему о взаимности работ для двух состояний системы при условии, что в обоих состояниях действует лишь по одной единичной силе, приложенной в состоянии (1) в точке “m”, а в состоянии (2) в точке “n” (см. рисунок).

Применяя теорему о взаимности возможных

Таким образом: удельное перемещение точки приложения первой единичной силы по ее направлению, возникающее при действии второй единичной силы, равно удельному

40