
8447
.pdf
|
|
40 |
dm = ρ · 2πrhdr |
и |
dJ = 2πhρr3dr. |
Тогда момент инерции сплошного цилиндра
R
J = ∫ dJ = 2πhρ∫ r3dr = 12 πhR 4ρ
0
но так как πR2h – объем цилиндра, то его масса m = πR2hρ, а момент инерции
J = 12 mR 2
Если известен момент инерции тела относительно оси, проходящей через
его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно
любой оси вращения равен моменту его инерции JС относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы тела на квадрат расстояния а между осями:
|
|
|
J = JC + ma2 |
(51) |
||
В заключение приведем значения моментов инерции (табл.1) для |
||||||
некоторых тел (тела считаются однородными, m - масса тела). |
||||||
|
|
|
|
|
|
Т а б л и ц а 1 |
|
Тело |
|
Положение оси |
Момент |
||
|
|
вращения |
инерции |
|||
|
|
|
||||
Полый |
тонкостенный |
Ось симметрии |
|
mR2 |
||
цилиндр радиуса R |
|
|
|
|
|
|
Сплошной цилиндр или |
То же |
|
|
12 mR 2 |
||
диск радиуса R |
|
|
|
|
|
|
Прямой тонкий стержень |
Ось |
перпендикулярна |
112 ml2 |
|||
длиной l |
|
стержню |
и |
проходит |
|
|
|
|
через его середину |
|
|||
|
|
|
|
|||
Прямой тонкий стержень |
Ось |
перпендикулярна |
13 ml2 |
|||
длиной l |
|
стержню |
и |
проходит |
|
|
|
|
через его конец |
|
|
||
Шар радиуса R |
Ось |
проходит через |
2 5 mR 2 |
|||
|
|
центр шара |
|
|
|
|
4.2.Кинетическая энергия вращения |
|
|
||||
Все реально существующие твердые тела под влиянием приложенных к ним сил деформируются, т. е. тем или иным образом изменяют свою форму.
Для упрощения дальнейших рассуждений введем понятие абсолютно твердого тела. Абсолютно твердым телом называется тело, которое ни при каких
41
условиях не может деформироваться и при всех условиях расстояние между двумя точками, или, точнее, между двумя частицами этого тела остается постоянным. В дальнейшем мы будем рассматривать только такого рода тела.
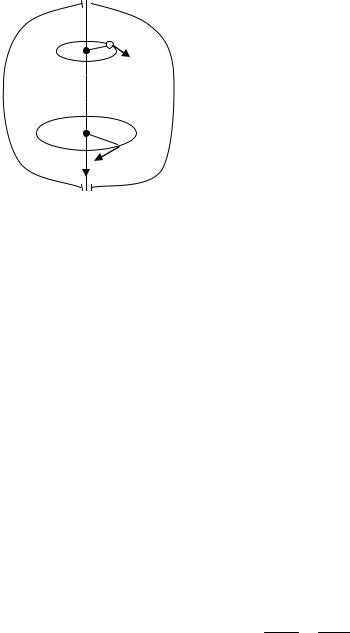
Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси ОО, проходящей через него (рис. 21). Мысленно разобьем это тело на маленькие объемы с элементарными массами m1, m2, …, m n, находящиеся на расстоянии r1, r2, …, r n от оси вращения. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами
mn опишут окружности различных радиусов г„ и
0 |
|
|
|
будут иметь различные линейные скорости υn. Но |
|
|
|
|
|
r1 |
|
|
|
m1 |
|
так как мы рассматриваем абсолютно твердое |
|
|
|
|
|
||
|
|
|
|
тело, то угловая скорость вращения этих |
|
r1 |
|
v1 |
|
||
|
|
объемов одинакова: |
|||
|
|
|
|
|
|
rn
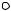 mn
mn
vn
0
Рис. 21
или
ω = υ1 / r1 = υ2 / r2 = ... = υn / rn |
(52) |
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
|
|
|
|
T = |
m1υ12 |
+ |
m2 υ22 |
+ ... + |
mn υn2 |
, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
тв |
2 |
2 |
2 |
|
|||
|
|
|
|
|
|
|
|||||
|
|
n |
m |
υ2 |
|
|
|
|
|
|
|
T |
= |
∑ |
i |
i |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
тв |
|
|
|
|
|
|
|
|
|||
|
|
i=1 |
|
|
|
|
|
|
|
||
Используя выражение (52), получим
Tтв |
= ∑ mi ω |
2 |
ri2 = ω |
2 |
= Jω |
2 |
|
(53) |
|||
|
|
∑mi ri2 |
. |
||||||||
|
n |
|
|
|
|
n |
|
|
|
|
|
|
i=1 2 |
|
2 |
i=1 |
2 |
|
|
|
|||
Из сравнения формулы (53) с выражением (31) для кинетической энергии тела, движущегося поступательно (Т = mυ2/2), следует, что момент инерции вращательного движения — мера инертности тела. Чем больше момент инерции, тем большую энергию нужно затратить для достижения данной скорости.
Формула (53) справедлива для тела, вращающегося вокруг неподвижной оси. Для тела (колеса), катящегося по горизонтальной поверхности, энергия движения будет складываться из энергии поступательного движения и энергии вращения:
= mυ2 + Jm2
T
2 2
где m — масса катящегося тела, υ — скорость поступательного движения, J — момент инерции тела, ω — скорость вращательного движения.
|
|
|
42 |
|
|
|
|
4.3.Уравнение динамики вращательного движения твердого тела |
|||||||
Если тело, закрепленное на оси, приводится во вращение какой-либо |
|||||||
силой, то кинетическая энергия вращения возрастает на величину затраченной |
|||||||
|
|
|
работы. Работа зависит от действующей силы |
||||
|
|
|
и от произведенного ею перемещения, однако |
||||
dφ |
B |
|
выражение |
работы |
для |
смещения |
|
r |
dS |
материальной |
точки |
при |
вращательном |
||
0 |
α |
|
|||||
|
движении неприменимо, так как в данном |
||||||
|
|
||||||
l |
|
|
случае перемещение угловое. |
|
|||
|
α |
|
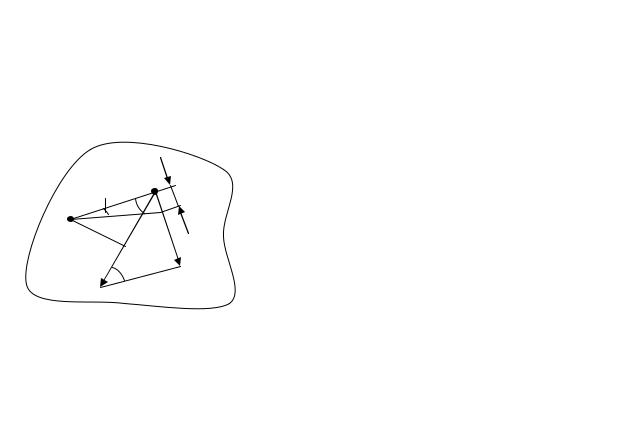
Найдем выражение для работы при вращении |
||||
F |
|
|
тела (рис. 22). Пусть сила F приложена в точке |
||||
|
|
В, находящейся от оси вращения на |
|||||
|
|
|
|||||
|
Рис. 22 |
|
расстоянии r, |
α — |
угол между направлением |
||
|
|
силы и радиусом вектором. Так как тело |
|||||
|
|
|
|||||
|
|
|
абсолютно твердое, то работа этой силы равна |
||||
работе, затраченной на поворот всего тела. При повороте тела на малый угол dφ |
|||||||
точка приложения В проходит путь ds = rdφ и работа равна произведению |
|||||||
проекции силы на направление смещения на величину смещения: |
|
||||||
dA = F sin α · rdφ |
(54) |
Величина |
|
M = Fr sin α |
(55) |
называется моментом силы относительно оси вращения;
r sin α = l
есть кратчайшее расстояние между линией действия силы и осью вращения и называется плечом силы. Момент силы равен произведению силы на ее плечо:
М=Fl
Момент силы — величина векторная. Так как l = r sin α , то вектор
М = [rF].
Его направление перпендикулярно плоскости, в которой расположен вектор силы, и он определяется по правилу правого винта.
Подставляя (55) в (54), получим, что работа при вращении тела равна произведению момента действующей силы на угол поворота:
dA = Mdφ

43
Работа при вращении тела идет на увеличение его кинетической энергии:
dA =dT, |
|||
но |
|
|
|
Jω2 |
|
|
|
dT = d |
|
|
= Jωdω |
|
|||
2 |
|
|
|
поэтому
Mdω = Jωdω
или
M dω = Jω dω
|
|
dt |
dt |
||
Учитывая, чтоω = |
dϕ |
, получим |
|
||
|
|
||||
|
dt |
|
|||
|
|
M = J |
dω |
= Jε |
(56) |
|
|
|
|||
|
|
|
dt |
|
|
В векторной форме |
|
||||
|
|
M=Jε |
(57) |
||
т. е. момент силы, действующей на тело, равен произведению момента инерции тела на угловое ускорение. Уравнение (57) представляет собой уравнение динамики вращательного движения твердого тела относительно
неподвижной оси.
4.4.Момент количества движения и закон его сохранения
При сравнении законов вращательного и поступательного движений усматривается аналогия между ними, только во вращательном движении вместо силы выступает ее момент, роль массы играет момент инерции. Какая же величина будет аналогом количества движения тела? Ею является момент
количества движения тела относительно оси.
Моментом количества движения (моментом импульса) Li отдельной частицы тела массой mi называется произведение расстояния ri от оси вращения до частицы на количество движения (импульс) mivi этой частицы:
Li = miυiri (58)
Момент импульса твердого тела относительно оси есть сумма моментов количества движения отдельных частиц:
|
44 |
|
|
n |
|
L = ∑ mi υi ri |
|
|
|
i=1 |
|
Так как для вращательного движения υi=ωri, то |
||
n |
n |
|
L = ∑ mi ri2 |
ω = ω∑ mi ri2 |
= Jω |
i=1 |
i=1 |
|
т.е. |
|
|
L = Jω |
|
(59) |
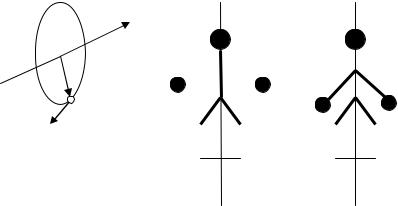
Таким образом, момент количества движения твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость. Момент количества движения твердого тела — это вектор, направленный по оси вращения так, чтобы видеть с его конца вращение, происходящим по часовой стрелке (рис. 23).
|
|
|
|
|
|
|
|
|
|
|
|
|
J1>J2 |
|
|
|
|||||||||
|
|
ω1 |
|
|
|
|
ω1< ω2 |
ω2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 24 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Продифференцируем уравнение (59) по времени: |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
dL |
|
|
= J |
dω |
= Jε = M |
|
|
|
||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|||||||||
или в векторной форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
dL |
= M |
(60) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|||||||||||
Уравнение (60) — еще одна форма уравнения (закона) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента количества движения твердого тела относительно оси вращения равна моменту сил относительно той же оси.
Если мы имеем дело с замкнутой системой, то момент внешних сил М = 0
и
45
dL |
= 0 , |
или |
L = const, |
т.е. |
|
||||
dt |
|
|
|
|
|
|
Jω = const |
|
(6ё) |
Выражение (61) представляет собой закон сохранения момента количества движения: момент количества движения замкнутой системы
сохраняется, т. е. не изменяется с течением времени.
Продемонстрировать сохранение момента количества движения можно с помощью скамьи Жуковского. Пусть человек„ стоящий на скамье, которая без трения вращается вокруг вертикальной оси, и держащий в поднятых на уровни плеч руках гири (рис. 24), приведен во вращение с угловой скоростью ω1. Человек обладает некоторым моментом количества движения, который сохраняется. Если он опустит руки, то его момент инерции уменьшится, в результате чего возрастет угловая скорость ω2 его вращения. Аналогично, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения.
Краткие выводы
∙Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
∙Момент инерции тела относительно оси вращения – это физическая величина, равная сумме произведений масс n материальных точек тела на
квадраты их расстояний до рассматриваемой оси:
n
J z = ∑mi ri 2 .
i=1
∙Момент инерции тела Jz относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:
J z = J c + ma2 .
∙При вращении абсолютно твердого тела вокруг неподвижной оси z его кинетическая энергия равна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости:
|
|
|
|
|
|
= |
J |
z |
ω 2 |
|
|
|
|
|
|
|
Ek вр |
|
|
. |
|
|
|||
|
|
|
|
|
2 |
J zω 2 |
||||||
|
|
|
|
|
|
|
|
|
||||
∙ |
|
|
= |
|
mv2 |
|
|
|
Ek вр = |
|||
Из сравнения формул |
Ek |
|
|
|
и |
|
|
следует, что момент |
||||
2 |
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
инерции – мера инертности тела при вращательном движении.

46
∙ Работа вращения тела идет на увеличение его кинетической энергии и определяется выражением dA = M z dϕ , где Mz – момент сил относительно оси вращения z.
∙Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z (аналог второго закона Ньютона) имеет вид:
M z = J z ε = dLz , dt
где Lz – момент импульса твердого тела относительно оси z.
∙ В замкнутой механической системе момент внешних сил относительно
неподвижной оси Mz=0 и dLz = 0 , откуда Lz=const – закон сохранения dt
момента импульса. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.
Вопросы для самоконтроля и повторения
1.Что называется моментом инерции тела? Какова роль момента инерции во вращательном движении?
2.Сформулируйте теорему Штейнера. От чего зависит момент инерции тела?
3.Что называется моментом силы относительно неподвижной точки? Относительно неподвижной оси? Как определяется направление момента силы?
4.Что такое момент импульса твердого тела? Как определяется направление момента импульса?
5.Какова формула для кинетической энергии тела, вращающегося вокруг неподвижной оси? Как определяется работа при вращении тела?
6.Выведите и сформулируйте уравнение динамики вращательного движения твердого тела.
7.Сформулируйте закон сохранения момента импульса. В каких системах он выполняется?
8.Сопоставьте основные величины и уравнения динамики поступательного и вращательного движений.
47
Часть 2. Основы термодинамики и молекулярной физики
1. Основные положения
1.1.Исходные положения термодинамики и молекулярной физики
Термодинамику и молекулярную физику объединяет то, что оба эти раздела физики изучают законы тепловой формы движения материи, однако подходы к решению этой задачи существенно различны.
Молекулярная физика является атомистической теорией тепловой формы движения материи. В основе этой теории лежат следующие положения:
−все тела состоят из большого количества весьма малых частиц - молекул;
−молекулы всякого вещества находятся в хаотическом движении, не имеющем какого-либо преимущественного направления. Интенсивность движения молекул зависит от температуры вещества.
Считая, что движение отдельных молекул подчиняется законам механики, и, пользуясь статистическим методом, молекулярная физика ставит своей целью объяснить наблюдаемые тепловые явления как суммарный результат движения молекул. Можно провести аналогию между методом исследования, используемым в молекулярной физике, и социологическим опросом населения, который, исходя из изучения мнения отдельных избирателей, стремится предсказать результат выборов.
Термодинамика - это макроскопическая теория тепла. В отличие от молекулярной физики она не использует какие-либо представления о структуре тел. Термодинамика оперирует только с измеряемыми на опыте величинами (объем, давление и.т.п.) и опирается на два принципа:
−положение о постоянстве энергии изолированной системы;
−факт односторонности самопроизвольного перехода теплоты от нагретых тел к холодным.
Эти принципы являются обобщением наблюдаемых природных явлений. Из этих принципов термодинамика выводит все основные свойства тел.
Подходя к решению одной и той же задачи с разных позиций, молекулярно-кинетический и термодинамический методы исследования дополняют друг друга, в чем мы вскоре убедимся на конкретных примерах.
1.2.Масса и размеры молекул
Для того, чтобы измерить какую-либо величину, нужно сравнить ее с другой величиной, которая принята за эталон (или за единицу измерения). Поскольку массы молекул очень малы, для их измерения удобно взять также малую единицу измерения. За единицу измерения масс в молекулярной физике принимают одну двенадцатую (1/12) часть атома 12С (так обозначается изотоп
48
углерода с массовым числом 12). Эта масса mед называется атомной единицей массы.
Массы различных молекул принято характеризовать относительной молекулярной массой вещества M r , которая равна отношению массы молекулы данного вещества m к атомной единице массы: M r =m/ mед . Для краткости эту величину часто называют молекулярной массой, однако следует помнить, что эта величина является безразмерной величиной, а, зная ее, массу молекулы данного вещества можно вычислить согласно формуле m = M r × mед .
Далее для описания количества вещества часто будет использоваться понятие - моль. Молем называется количество какого-либо вещества, в котором содержится столько же молекул, сколько их в 0,012 кг изотопа углерода 12С .
Очевидно, что моли всех веществ содержат одно и то же число молекул, которое принято обозначать N a . Величина N a является фундаментальной
величиной и называется числом Авогадро. Опытным путем удалось найти, что число Авогадро равно:
N a = 6.022 ×1023 моль−1 .
Таким образом, можно сказать, что моль - это такое количество вещества, в котором содержится число Авогадро молекул.
Массу одного моля вещества называют молярной массой и обозначают буквой μ . Нетрудно сообразить, что для того, чтобы найти молярную массу, нужно массу одной молекулы умножить на число Авогадро:
μ = m × N a = M r × mед × N a .
Эта формула справедлива для любых веществ, в том числе и для углерода 12С , в случае которого молярная масса, как сказано ранее, равна 0,012кг. В случае углерода M r =12, что очевидно. В результате, все величины, входящие в последнюю формулу, кроме mед являются известными. Поэтому эту формулу, записанную для углерода, можно использовать для определения величины
|
mед = |
|
μ |
|
= |
|
0.001кг / моль |
= 1,66 ×10−27 кг . |
|||||
|
M r × |
|
|
|
|
|
|
|
|||||
|
|
N a 6,022 ×1023 моль−1 |
|
|
|||||||||
Из |
последней формулы |
следует, |
что произведение двух констант |
||||||||||
mед × N a |
= 0.001кг / моль . Подставляя это значение в формулу (1.1), получим: |
||||||||||||
|
|
|
μ = 0,001× M r |
|
кг |
= M r |
|
г |
. |
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
моль |
моль |
||||
Таким образом, мы |
пришли |
к |
|
важному |
выводу, что масса моля, |
||||||||
выраженная в граммах, численно равна относительной молекулярной массе. Однако следует иметь в виду, что в то время, как M r - величина безразмерная, μ имеет размерность кг/моль (или г/моль).
Вывод: на практике нет необходимости вычислять молярную массу по формуле (1.1) - достаточно взять относительную молярную массу и умножить на 0,001. Результат получим в кг/моль.
49
1.3.Основные понятия термодинамики
Здесь мы поясним, что понимается под различными терминами, используемыми в термодинамике. К основным понятиям термодинамики относятся: система, состояние системы, процесс, температура, внутренняя энергия, работа, количество теплоты и т.п. Часто смысл этих понятий интуитивно ясен, тем не менее ниже мы поясним, что понимается в термодинамике под каждым из этих терминов. Предлагаем вам, прочитав название очередного термина, попытаться самостоятельно сформулировать, что вы понимаете под ним, а потом прочитать его толкование и обратить внимание на то, в чем ваше понимание не совсем точно. В процессе изучения термодинамики рекомендуем вновь просмотреть толкование термина, смысл которого вам покажется не совсем ясным.
СИСТЕМОЙ (или термодинамической системой) называют любое макроскопическое тело или совокупность тел, свойства которых изучаются. Простейшим примером системы является газ, в качестве более сложного примера системы приведем жидкость и находящийся с ней в равновесии пар. Тела, не входящие в рассматриваемую систему, называются внешними телами, или окружающей средой.
∙Система называется изолированной, если она не взаимодействует с внешними телами. Строго говоря, изолированных систем не существует. Это очередная научная абстракция (как, например, понятие материальной точки), однако это допущение в каком-то конкретном случае может удовлетворительно описывать ситуацию.
∙Система является не изолированной, если она взаимодействует с
внешними телами. Подчеркнем, что одна и та же система может являться изолированной или не изолированной в зависимости от конкретных условий. Например, газ под поршнем может считаться изолированной системой, если поршень закреплен, а при подвижном поршне система будет, вообще говоря, не изолированной, поскольку возможно взаимодействие с атмосферным газом через силу давления, оказываемую на поршень.
СОСТОЯНИЕ системы определяется совокупностью измеряемых физических величин, называемых параметрами состояния. Параметрами
состояния являются температура T, объем V, давление P.
∙ Равновесное состояние - это такое состояние, которое в изолированной системе сохраняется бесконечно долго. Равновесные состояния можно характеризовать определенными значениями термодинамических параметров, которые при этом постоянны по всему объему системы. При этом между
термодинамическими параметрами системы имеется определенная функциональная зависимость, выражаемая уравнением состояния P=f(V,T).
Конкретный вид функции f определяется из опыта. Далее мы будем иметь дело с уравнением состояния идеального газа. Равновесное термодинамическое состояние системы наглядно можно изобразить точкой в плоскости
