
8444
.pdf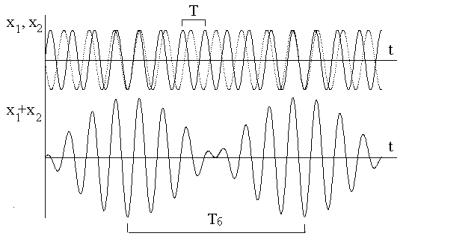
150
Поэтому для амплитуды результирующего колебания можно использовать формулу (32) с заменой
φ 2 − φ 1 = ω t ,
тогда
A2 = 2a2 (1+ cos ( ω t)) = a2 cos2 ( ωt / 2) ,
Таким образом, результирующая амплитуда медленно меняется со временем по закону
A(t ) = a |
|
cos( ω t / 2) |
|
. |
(35) |
|
|
Само колебание x(t) уже не будет гармоническим; оно представляет собой произведение этой амплитуды на гармоническую функцию 85 cos (ω t ) . Такие колебания называются биениями (см. рис. 10).
Рис. 10.
Сложение колебаний с близкими частотами. Верхняя картинка - осциллограммы складываемых колебаний, нижняя - их сумма.
Период биений обратно пропорционален разности частот слагаемых
Tδ = 2π / |
|
ω . |
(36) |
||
Действительно, период функции |
|
cos z |
|
|
в два раза меньше, чем у функции cos |
|
|
||||
z , поэтому период функции (35) определяется формулой (36).
Метод биений используется для нахождения неизвестной частоты сигнала. На вход осциллографа подаётся сигнал неизвестной частоты и сигнал лабораторного генератора, частоту которого можно изменять. Настраивают
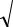
151
генератор так, чтобы увидеть картинку биений и далее плавно подстраивают в сторону увеличения их периода. При Tδ → ∞ ω → 0 , и мы, тем самым, настроим свой генератор на частоту неизвестного сигнала.
1.10.Сложение взаимно перпендикулярных колебаний
Рассмотрим теперь сложение перпендикулярных гармонических колебаний. В качестве механической модели можно представить груз, закрепленный на двух расположенных перпендикулярно пружинах. Электрические сигналы, подаваемые на входы x и y осциллографа (при выключенной развертке) дают на экране картинку результирующей траектории такого движения. Эта траектория в общем случае весьма сложна; рассмотрим сначала сложение колебаний одинаковой частоты.
Предположим, что точка участвует в двух колебательных движениях и запишем её координаты в виде
x(t ) = Ax cos(ω t ) , y(t ) = Ay cos(ω t + φ ) . |
(37) |
Для получения траектории движения точки из этих уравнений нужно
исключить время (в данном случае ω t |
). Запишем |
|
|
|||||
|
cos(ω t) = x / Ax , |
cos(ω t + φ) = y / Ay . |
|
(38) |
||||
Используем разложение косинуса |
|
|
|
|
|
|||
|
cos(ω t + |
φ ) = cos(ω t ) cos( φ ) − sin(ω t ) sin( φ ) , |
|
|||||
или, учтя (38), |
|
|
|
|
|
|
|
|
|
y / Ay = x / Ax cos( φ ) − |
|
|
sin( φ ) . (39) |
|
|||
|
|
1 − ( x / Ax ) 2 |
|
|||||
Возведя |
уравнение |
(39) |
в |
квадрат |
и |
используя |
тождество |
|
sin 2 ( |
φ ) + cos2 ( φ ) = 1 |
, получим уравнение траектории |
|
|||||
x 2 |
+ |
y 2 |
− |
2 xy |
cos( φ) = sin ( φ) |
. |
(40) |
||
|
2 |
|
2 |
|
|||||
A |
|
A |
|
Ax Ay |
|||||
x |
|
y |
|
|
|
||||
|
|
|
|
|
|
|
|
||
Траектория, описываемая этим уравнением, представляет собой эллипс, повернутый в общем случае на некоторый угол относительно координатных осей.
Рассмотрим характерные частные случаи. Пусть разность фаз колебаний равна π / 2 . Тогда из формулы (40) получаем
152
x 2 |
+ |
y 2 |
= 1 |
|
|
|
2 |
2 |
. |
(40a) |
|||
|
|
|||||
Ax |
|
Ay |
|
|
|
Это уравнение эллипса, ориентированного по координатным осям (см. рис. 11,
кривая 1). Положим теперь φ = 0 , или φ = π . При этом из формулы (40) получим уравнение отрезков прямых (кривые 2, 3, соответственно).
y = |
Ay |
x , ( x ≤ Ax , y ≤ Ay ) . |
(40б) |
|
Ax |
||||
|
|
|
Рис. 11.
Траектории движения при сложении перпендикулярных колебаний равных частот. Для кривой 4 разность фаз π / 4 .
Если частоты складываемых колебаний не равны, то в общем случае результирующая траектория незамкнута (точка постепенно «закрашивает»
прямоугольник со сторонами 2Ax , 2Ay ). Если частоты кратные, т.е.
ω y / ω x = m / n ,
где m и n - целые числа, то получаются замкнутые кривые состоящие из пересекающихся петель, называемые фигурами Лиссажу (см. рис.12).
Рис. 12а - отношения частот 1/2 . |
Рис.12б - отношение частот 3/2 . |
153
Сложение перпендикулярных электрических колебаний, выполняемое с помощью осциллографа, также используется для нахождения неизвестной частоты сигнала. На вход X осциллографа подаётся исследуемый сигнал, а на вход Y - сигнал лабораторного генератора. Настраивают генератор так, чтобы увидеть на экране эллипс; при этом частоты обоих сигналов совпадут, значит искомая частота определена.
Вопросы для самоконтроля и повторения
11.Какое движение называется колебательным? Какие колебания называются свободными, гармоническими, вынужденными?
12.Дайте определение параметров колебательного процесса (амплитуда, фаза, период, частота, циклическая частота).
13.Что называется гармоническим осциллятором? Приведите примеры гармонического осциллятора.
14.Выведите дифференциальное уравнение свободных колебаний пружинного маятника. По каким формулам определяются периоды гармонических колебаний пружинного, физического и математического маятников?
15.Выведите дифференциальное уравнение свободных электромагнитных колебаний в контуре. По какой формуле определяется период колебаний в контуре с малыми омическими потерями?
16.Какие колебания называются затухающим? Запишите дифференциальное уравнение затухающих колебаний и его решение.
17.Что такое логарифмический декремент затухания, добротность системы? В чем заключается физический смысл этих величин?
18.Какие колебания называются вынужденными? Запишите дифференциальное уравнение вынужденных колебаний и его решение.
19.Что называется, автоколебаниями? В чем их отличие от вынужденных колебаний? Приведите примеры автоколебательных систем.
20.Что называется, резонансом? Запишите выражения для циклической частоты и амплитуды колебаний при резонансе.
21.Что называется, переменным электрическим током? Выведите закон Ома для цепи переменного тока. От чего зависят индуктивное и емкостное сопротивления?
22.Каковы характерные признаки резонанса напряжений, резонанса токов? Нарисуйте векторные диаграммы цепей переменного тока в режимах последовательного и параллельного резонанса.
154
2. Волновые процессы
2.1.Основные определения. Классификация волн
Волновые процессы, или волны окружают нас повсюду: волны на воде - поверхностные волны, звуковые волны, электромагнитные волны (в частности, видимый свет, излучение тепла нагретым телом) — это далеко не
полный перечень волновых процессов. Мы ограничимся весьма кратким рассмотрением этого класса физических явлений.
Итак, волной называют колебание какой-то физической величины, распространяющееся в пространстве, т.е. волна — это бегущее колебание. Если колебание описывалось функцией одного аргумента - времени, то волна есть функция по крайней мере двух переменных - времени и пространственной координаты (в общем случае всех координат x, y, z ).
Геометрическое место точек пространства, где колебания имеют одинаковую фазу, называется волновой поверхностью, а первая (т.е. наиболее удаленная от источника) волновая поверхность - волновым фронтом. По форме волнового фронта различают плоские, сферические, цилиндрические
волны.
Плоские волны создаются плоским излучателем, имеющим достаточно большие размеры (формально - бесконечной плоскостью). Если такая волна распространяется вдоль оси x, то она описывается функцией двух переменных p(x;t) .
Сферические волны создаются источником сферической формы. Например, источником таких звуковых волн может служить динамик с
диффузором в виде шара. |
Заметим однако, что на больших расстояниях |
(значительно превышающих |
размеры источника) волна будет сферической |
при любой форме источника колебаний. Другими словами, источник колебаний малых размеров излучает сферические волны. Такие волны описываются функцией p(r;t) , где r - расстояние от источника.
Предположим, что источник совершает гармонические колебания частоты ν ( ν = 1 / T = ω / 2π ) , где T - период колебаний, ω - циклическая частота. Расстояние, пробегаемое волной за один период колебания называется длиной волны, т.е.
λ = c T = c / ν , |
(41) |
где c - скорость распространения волны.
По форме распространяющихся колебаний различают гармонические (в оптике их называют монохроматические) и негармонические волны. Последние можно представить суперпозицией гармонических.
По физической природе различают упругие (или звуковые) волны, поверхностные (например, волны на воде), электромагнитные и другие.
155
Естественно, характеристики перечисленных волновых процессов совершенно различны. Они различны и внутри любого одного типа волн; например, различна скорость звука в газах и жидкостях, свойства электромагнитных волн существенно зависят от их частоты. Однако, как и в случае колебаний, в математическом описании волн разных видов много общего.
По направлению колебаний различают волны продольные и поперечные. Для первых направление колебаний совпадает с направлением распространения волны, для вторых - эти направления взаимно перпендикулярны. Например, звук в газах - это продольные волны, электромагнитные волны - поперечные
2.2.Плоские и сферические волны
Предположим, что в плоскости x = 0 имеется источник совершающий колебания; например, для звуковых волн, это может быть плоскость диффузор громкоговорителя. Считаем эти колебания гармоническими с амплитудой A и циклической частотой ω
p(0; t ) = A sin(ω t ) . |
(42) |
|
При этом в упругой среде (газе, жидкости) |
колебания давления |
(или |
плотности), вызванные колебаниями источника |
p(0; t) , передаются от точки к |
|
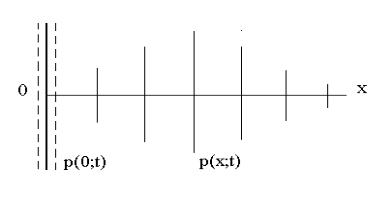
точке, и вдоль оси x побежит плоская волна p(x; t) , см. рис.13.
Рис.13. Распространение плоской волны.
Пренебрегая затуханием колебаний по мере их распространения, считаем,
что колебание, которое пришло в точку |
x в момент времени |
t - это то же, |
что было в точке x = 0 в момент времени |
t - τ , где τ = x / c - время пробега |
|
волны от нуля до точки x . Таким образом, с учетом (42) имеем |
|
|
p( x; t ) = p(0; t − τ ) = A sin[ω ( t − τ )] = A sin(ω t − kx) |
, |
|
где |
|
|
k = ω / c = 2π / λ |
|
(43) |
156
называется волновым числом (напомним, что λ - длина волны). Итак, плоская гармоническая волна, распространяющаяся вправо вдоль оси x со скоростью c описывается формулой
p( x; t ) = A sin(ω t − kx) . |
(44) |
Ясно, что для волны, бегущей влево в выражении (44) следует поставить знак + (т.к. изменится знак скорости).
Наблюдая волну (44) в фиксированной точке |
x = x1 , мы имеем |
гармоническое колебание, фаза которого зависит от выбранной точки |
|
p( x1 ;t) = A sin(ωt − φ1 ) , φ 1 = 2πx1 / λ |
(44а |
это осциллограмма плоской волны. Зафиксировав в (44) момент времени
t = t1 , получим гармоническую функцию координаты, называемую мгновенный снимок волны
p( x;t1 ) = A sin(ωt1 − 2π / λ x) . |
(44б) |
Период этой функции равен длине волны λ .
Предположим теперь, что в начале координат имеется точечный источник, совершающий гармонические колебания. Проводя аналогичные рассуждения, запишем уравнение вызванной им сферической волны в виде
p(r; t ) = A(r) sin(ω t − kr) , |
(45) |
где r - длина радиуса - вектора в точку наблюдения. Существенным отличием формулы (45) от (44) является то, что амплитуда здесь будет убывать по мере распространения даже в отсутствии потерь. В самом деле, площадь волнового фронта (сферы радиуса r ) растёт пропорционально квадрату радиуса, а энергия колебаний на каждой такой сфере должна быть одинакова. Поскольку энергия колебаний пропорциональна квадрату амплитуды , отсюда следует, что
A2 r 2 = const ,
а значит амплитуда сферической волны (45) должна |
меняться по закону |
A(r) = A0 / r , |
(46) |
где A0 - амплитуда колебаний источника. |
|
2.3.Волновое уравнение для плоских волн
Напомним, что гармоническое колебание является общим решением дифференциального уравнения (8), называемое уравнением гармонического осциллятора. Плоская волна (44) является общим решением дифференциального уравнения в частных производных

157
∂ 2 p − 1 ∂ 2 p = 0 |
, |
(47) |
∂ x 2 c2 ∂ t 2 |
которое называется волновым уравнением ( с - скорость распространения волны в данной среде). Действительно, дифференцируя (44) по x и по t , имеем
∂ 2 p |
= − A k 2 sin(ω t − kx) , |
∂ 2 p |
= − Aω 2 sin(ω t − kx) . |
(48) |
∂ x2 |
∂ t 2 |
Подставив (48) в (47) и учтя, что волновое число k = ω / c , получим тождество. Уравнение (47) возникает при решении многих физических проблем: оно получается из законов механики в задаче распространения колебаний смещения среды в твердом теле, из газовых законов при исследовании распространения колебаний давления в газе, из уравнений электродинамики в задачах распространения электромагнитных волн. Конечно, в разных задачах
физический смысл переменной p скорости c различен.
Отметим, что гармоническая волна (44) это лишь одно из его решений. Оказывается, ему удовлетворяет колебание любой формы, бегущее со скоростью с. В самом деле, пусть колебание источника представляет собой любую функцию времени , т.е. p(0;t) = f (t) . Тогда в точке x оно имеет вид
p(x;t) = f (t − x / c) .
Обозначим z = t − x / c и дифференцируя, имеем
p′′ = f ′′ |
, |
p′′ |
= 1 / c2 f ′′ |
(49) |
|
tt |
zz |
xx |
zz . |
||
Подставляя (49) в (44), мы вновь получаем тождество.
2.4.Звуковые волны
Звуковые волны в газе представляют собой бегущие колебания давления (или плотности ρ , поскольку, согласно уравнению состояния газа, p ρ ). Если
атмосферное давление равно pA , то полное давление в точке x , которую достигла плоская волна в момент времени t , будет
P(x;t)=pA+p (x;t) ,
где p(x;t) - малая добавка, определяемая формулой (44).

158
Человек слышит не любой звук, а примерно, в диапазоне частот от 20 герц до 20 килогерц. Колебания более низких частот называют
инфразвуком, а более высоких - ультразвуком.
Скорость распространения звуковых волн в газе зависит от плотности среды (а она связана с температурой) и определяется формулой
c = γ |
p |
= |
γ |
RT |
|
|
|
ρ |
μ |
, |
(50) |
||||
|
|
|
|||||
|
|
|
|
|
где γ - показатель адиабаты (для воздуха он равен 1,4), R - газовая постоянная, μ - молярная масса (для воздуха - 0,029 кг/моль). При нормальных условиях формула (50) даёт значение скорости звука
c ≈ 3 3 0 м/с .
Звуковые волны в твердых телах могут быть как продольными, так и поперечными (сдвиговыми). Скорость распространения звука в твердых телах зависит от их упругости и плотности и она значительно выше скорости звука в газах. В частности, скорость продольных волн в стержнях определяется формулой
c = |
|
E / ρ |
, |
(51а) |
|
а поперечных - формулой |
|
|
|
|
|
c = |
|
|
, |
|
|
|
G / ρ |
(51б) |
|||
где E - модуль упругости (модуль Юнга), G - модуль сдвига, материала. Например, для железа формула (51а) дает значение c = 5170 м/с.
Слуховое восприятие звуковых волн - громкость
интенсивности колебаний
I = p / S ,
ρ - плотность
зависит от
где |
p - средняя |
мощность колебаний, |
переносимая через площадь |
S. |
Интенсивность пропорциональна квадрату амплитуды колебаний, а наше |
||
восприятие громкости - логарифму интенсивности. Принятая в акустике единица измерения интенсивности звука - децибел ориентирована именно на логарифмическое восприятие. Скажем, если интенсивность в единицах системы СИ равна I (вт/ M 2 ), то в децибелах она равна
IdB = 10 lg( I / I0 ) (дБ) , |
(52) |

159
где I 0 - минимальная интенсивность, соответствующая порогу слышимости (примерно 10−12 вт/ M 2 ).
2.5.Электромагнитные волны
Электромагнитные волны представляют собой взаимно связанные колебания напряженности электрического и магнитного полей, распространяющиеся в пространстве. Источником электромагнитных волн являются движущиеся с переменной скоростью электрические заряды. Это могут быть хаотически движущиеся свободные электроны или ионы (в случае теплового излучения), переменный ток достаточно высокой частоты в проводнике (при излучении радиоволн), электроны, переходящие с верхних энергетических уровней на нижние (при излучении света газоразрядными трубками и лазерном излучении).
Электромагнитные волны могут распространяться в свободном пространстве (вакууме) или в средах, не проводящих электрический ток. В проводящей среде они вызывают движение зарядов, следовательно, их энергия превращается в тепло и волны быстро затухают. Скорость электромагнитных волн в вакууме
c » 3×108 M /c ,
её принято называть скоростью света. В среде с показателем преломления |
n |
|||||
скорость их меньше |
|
|
|
|
|
|
|
V =c / n , |
n = |
|
|
|
|
|
ε / μ |
(53) |
|
|||
Здесь |
ε - диэлектрическая, а μ |
- |
магнитная |
проницаемость. |
В |
|
диэлектрических средах, где, собственно, и могут распространяться волны,
μ = 1 .
Электромагнитные волны поперечные: если, например, волна бежит вдоль оси x , то колебания вектора напряженности электрического поля E направлены вдоль оси y , а колебания напряженности магнитного поля H - вдоль оси z (или наоборот). Соответствующие формуле (47) волновые уравнения здесь имеют вид
∂ 2 Ey |
− |
1 |
∂ 2 E y |
=0 |
, |
∂ 2 H |
z − |
1 |
∂ 2 H |
z =0 |
, (54) |
|
|
|
|
|
|
||||||
∂ x2 |
V 2 ∂ t 2 |
|
∂ x2 |
V 2 ∂ t 2 |
|
||||||
|
|
|
|
||||||||
где V =c / 
 ε .
ε .
