8440
.pdf
140
получаем тождество (т.е. равенство (8) выполняется в любой момент времени при ω = ω 0 ). Это означает, что общим решением дифференциального уравнения (8) является гармоническое колебание (2), циклическая частота которого
ω 0 = |
k / m |
. |
(9) |
Дифференциальное уравнение (8) называется уравнением гармонического осциллятора (oscillation - колебание). Оно имеет универсальный вид для любой системы, где возможны незатухающие гармонические колебания. Итак, частота собственных колебаний пружинного маятника определяется формулой
(9), а в общем случае она определяется |
свойствами самой колебательной |
системы. |
|
Выясним, от чего зависит амплитуда и начальная фаза. Положив в |
|
формуле (2) и в первой формуле (4) t = 0 , |
запишем |
x0 = x(0) = A sin φ , v0 = v(0) = Aω cos φ .
Отсюда можно выразить амплитуду и начальную фазу:
A2 = x02 + v02 / ω 2 , φ = arctg(ωx0 / v0 ) . |
(10) |
Таким образом, амплитуда и начальная фаза собственных колебаний определяется начальными условиями . В рассмотренном примере это начальное смещение груза и начальная скорость. В частности, если колебание возникает из-за начального смещения (начальная скорость равна нулю), то как видно из
(10), A = x0 |
, φ = π / 2 . |
Если колебание вызвано начальным толчком |
|
(заданием |
начальной |
скорости в положении равновесия), |
то |
A = v0 / ω , φ = 0 . |
|
|
|
1.4.Преобразование энергии в процессе гармонических колебаний
При любом колебательном процессе происходит периодическое преобразование энергии из одного вида в другой. В рассмотренной модели это потенциальная энергия деформированной пружины и кинетическая энергия груза. Они определяются выражениями
E p = k x2 / 2 = 1/ 2 kA2 sin2 (ω 0 t +φ )
Ek = mV 2 / 2=1/ 2mω0 2 A2 cos2 (ω0 t+φ) .
|
|
141 |
Поскольку k = mω 0 |
2 |
, коэффициенты перед sin2 (ω 0 t +φ ) и cos2 (ω 0 t + φ ) |
одинаковы. Складывая эти формулы (и учтя основное тригонометрическое тождество sin2 z + cos2 z = 1, z = ω t + φ ), получим
E p + Ek |
= 1 / 2 mω 0 |
2 A2 = const . |
(11) |
Таким образом, |
хотя потенциальная и |
кинетическая энергии |
|
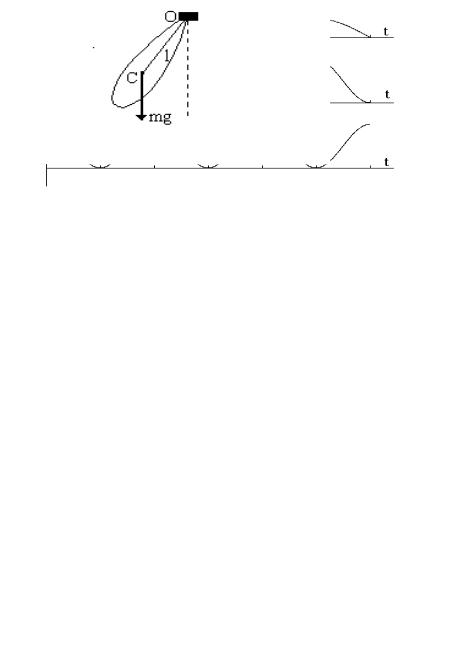
изменяются со временем (см. рис.3), полная энергия колебаний не зависит от времени и определяется выражением (11) .
Рис.3. Первая кривая - гармоническое колебание, вторая - |
его |
потенциальная энергия, третья - кинетическая энергия. |
|
Видно, что максимум кинетической энергии соответствует минимуму |
|
потенциальной и наоборот, а сумма их остается постоянной. |
|
Сохранение энергии обусловлено тем, что мы пока не учли трение. |
Хотя |
формула (11) получена для простейшей модели колебательного движения,
заметим, что энергия колебаний в любой системе пропорциональна квадрату амплитуды и квадрату частоты.
1.5.Физический маятник
Физический маятник - это любое тело, имеющее ось вращения, не совпадающую с его центром масс (см., например, рис.4) . Здесь точка С - центр масс, l - его расстояние до оси вращения О.
Рис.4. Физический маятник.
142
При выведении из состояния равновесия он будет совершать колебания, которые при небольших амплитудах будут гармоническими. Покажем это.
Исходим из основного уравнения динамики вращательного движения |
|
|
|
Iβ = M , |
(12) |
где |
I − момент инерции, M - момент сил, β - угловое ускорение. |
Из рис.4 |
ясно, что вращающий момент создает только сила тяжести и |
|
|
|
M = − mg l sinα , |
|
где |
α - текущий угол отклонения, зависящий от времени. Поскольку угловое |
|
ускорение β есть вторая производная от α , подставив все в (12), запишем
α ′′ + mgl / I sinα = 0 . |
(13) |
|
Обозначив mgl / I =ω 0 |
2 , мы получим дифференциальное |
уравнение |
«похожее» на уравнение гармонического осциллятора (8). Конечно, это совсем другое уравнение и гармоническое колебание не является его решением, а значит колебания физического маятника не являются в общем случае гармоническими. Однако, если они достаточно малы, так, что можно
считать sinα ≈ α , то уравнение (13) превратится в (8) |
(разумеется |
для |
||
текущего значения угла α (t) ), где циклическая |
|
|
||
частота собственных колебаний определяется формулой |
|
|
||
ω 0 = |
|
. |
|
|
mgl / I |
(14) |
|
||
Следовательно, период колебаний равен |
|
|
||
T = 2π / ω 0 = 2π |
I / mgl |
. |
(15) |
В частности, для математического маятника ( для него момент инерции
I = ml 2 ) из (15) получается хорошо знакомая вам формула
T = 2π 
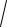l / g .
1.6.Затухающие колебания
Любые собственные колебания со временем затухают из-за потерь энергии. В механических системах основной причиной таких потерь является вязкое трение. Вязкое трение - это трение движущегося тела о среду. При малых скоростях движения она пропорциональна скорости
143 |
|
FTp =− μV =− μ x′ . |
(16) |
где μ - коэффициент вязкого трения (он зависит от вязкости среды, размеров и формы тела). Вернемся к простейшей модели - пружинному маятнику (см. П.3) и учтем в формуле (7) кроме упругой силы силу трения (16). При этом уравнение осциллятора (8) запишем в виде
x′′ + 2β x′ + ω 0 |
2 x = 0 . |
(17) |
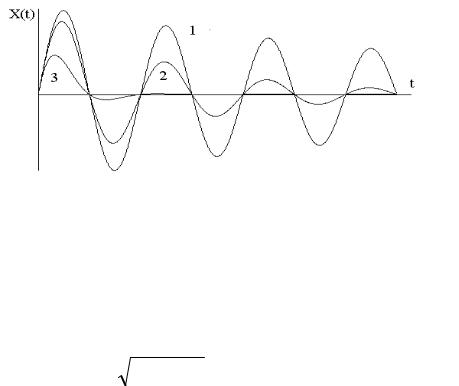
где β = μ / 2m - называется коэффициентом затухания. Решением уравнения (17) являются затухающие колебания (см..рис.5), т.е. колебания, амплитуда которых уменьшается со временем
x(t ) = A(t ) sin(ω |
1 |
t + φ ) , A(t ) = A |
e− β t |
(18) |
|
|
|
0 |
. |
||
Это можно проверить, дифференцируя |
(18) |
и подставляя |
x , x ′, x′′ в |
||
уравнение (17). |
|
|
|
|
|
Рис.5.
Осциллограммы затухающих колебаний. Коэффициенты затухания для этих кривых связаны соотношением β1 < β 2 < β 3 . Кривая 3 соответствует границе апериодического режима.
Частота затухающих колебаний несколько меньше частоты незатухающих
ω 1 = ω 0 |
2 − β 2 . |
(19) |
При сильном затухании, (если β ³ ω 0 - сильно вязкая среда) колебательный режим превращается в апериодический (колебание затухает на промежутке времени, меньшем периода, т.е. колебаний в сущности нет).
|
144 |
Кроме коэффициента β приняты и другие характеристики затухания: |
|
τ = 1/ β |
- характерное время затухания (время уменьшения амплитуды в e |
раз), |
κ = β T - логарифмический декремент затухания (T - период |
колебаний), Q = ω 0 / 2β - добротность колебательной системы. Последние две характеристики безразмерны; слабое затухание соответствует малому значению декремента, или большой ( Q>>1 ) добротности.
1.7.Колебательный контур. Собственные колебания
Рассмотрим теперь электромагнитные колебания. Заметим предварительно, что электромагнитные колебания, распространяющиеся в пространстве - электромагнитные волны - это неотъемлемая составляющая современной цивилизации: радио, телевидение, средства связи, радиолокация, интернет - вот основные формы их применения.
Рис. 6. Колебательный контур.
Колебательный контур состоит из катушки индуктивности L , конденсатора C и сопротивления R (см. рис. 6 ). Оно, как правило, не ставится специально, а представляет собой сопротивление катушки и проводов.
Рассмотрим сначала собственные колебания, полагая, что клеммы для подключения входного сигнала замкнуты, а конденсатор заряжен в момент времени t = 0 включён в контур. Он разряжается через катушку, но возникающая в ней при прохождении тока ЭДС самоиндукции замедляет этот процесс. Спустя некоторый (в действительности, очень малый) промежуток времени конденсатор перезарядится (полярность пластин поменяется), и ток пойдет в обратном направлении. Так возникает колебательный режим. Из-за потерь энергии на сопротивлении колебания будут затухать. Заметим, что здесь происходят колебания заряда конденсатора Q(t), напряжения на конденсаторе U(t), силы тока I(t).
Запишем закон Кирхгофа (сумма падений напряжений на всех элементах контура равна сумме ЭДС), учтя, что мы имеем ЭДС самоиндукции,
определяемую формулой |
|
Ei = − LI ′ |
(20) |
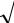
145 |
|
( I ′ - производная по времени от силы тока). |
Он имеет вид |
IR +U = − LI ′ . |
(21) |
Учтём также, что напряжение на конденсаторе связано с его зарядом формулой U = Q / C . Следовательно,
U ′ = I / C , I ′ = CU ′′ . |
(22) |
Поэтому продифференцировав уравнение (21), и используя (22), получим уравнение затухающих колебаний для напряжения
U ¢¢ + 2β U ¢ +ω 0 |
2U = 0 , |
(23) |
совпадающее по форме с уравнением для механических колебаний (17). Частота собственных колебаний и коэффициент затухания здесь определяются формулами
ω 0 =1 / |
LC |
, β = R / 2 L , |
(24) |
а частота затухающих колебаний связана с ω 0 |
формулой (19). Отметим, что |
||
затухание электрических колебаний обусловлено сопротивлением контура.
1.8.Вынужденные колебания. Резонансная кривая
Напомним, что вынужденные колебания возникают под действием периодической внешней силы. Роль такой «силы» для электромагнитных колебаний в контуре на рис.6 играет гармоническое напряжение v(t), приложенное к клеммам (синусоидальный сигнал, подаваемый с генератора). Положим, что
v(t ) = a sin(ωt ) |
(25) |
и запишем закон Кирхгофа, как делали выше. Только теперь ЭДС будет складываться из ЭДС самоиндукции (20) и внешнего сигнала (25). Используя, как и ранее, (21), (22), получим уравнение вынужденных колебаний напряжения на конденсаторе
U ¢¢+ 2βU ¢ +ω0 |
2U =ω02 a ×sin(ωt) , |
(26) |
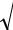
146
которое отличается от (23) только правой частью. Если входное напряжение действует в течении времени большем времени затухания собственных
колебаний, то решением дифференциального уравнения |
(26) будет колебание |
с частотой, равной частоте внешней силы ω . |
|
Для того, чтобы найти его амплитуду A , представим напряжение в |
|
виде |
|
U (t)=Acos(ω × t+φ ) |
(27) |
и (продифференцировав нужное количество раз) подставим в (26). Косинус суммы, входящий в (27) разложим по формуле
cos(ω t+φ )=cos(ω t)cos φ -sin(ω t) sin φ . |
(28) |
Собрав коэффициенты при cos(ωt) и sin(ω t) в левой части полученного из (26) уравнения, приравниваем их к соответствующим коэффициентам в его правой части. Чтобы иметь тождество, коэффициент при косинусе должен
равняться нулю, а при синусе - ω 20 a . Таким образом находим амплитуду
A2 = |
|
a 2ω 04 |
|
|
||
(ω 2 |
− ω 0 |
2 )2 + 4β 2ω 2 . |
(29) |
|||
|
||||||
Отсюда следует, что амплитуда вынужденных колебаний пропорциональна амплитуде входного сигнала (это вполне естественно), но и
существенным образом зависит от его частоты. Эта зависимость не монотонна и имеет максимум на частоте
|
|
|
|
ω ≡ ω p = ω 02 − 2β 2 , |
(30) |
||
которую называют резонансной частотой (при малом затухании она близка к частоте собственных колебаний) Зависимость амплитуды от частоты (корень квадратный из выражения (29) ) называют резонансной кривой. При этом максимальная (или резонансная) амплитуда определяется выражением
Ap = aω 0 / 2β ≡ Qa |
(31) |
(напомним, что Q = ω 0 / 2β - добротность колебательной системы). Отсюда ясно, что добротность показывает во сколько раз резонансная амплитуда превосходит амплитуду внешней «силы». Чем меньше затухание β , или больше добротность, тем сильнее выражен максимуму на резонансной кривой и тем она острее (см. рис.7).
147
Рис.7.
Резонансные кривые. Для приведенных графиков β 1 < β 2 < β 3 .
Резонанс, как свойство системы достаточно сильно “ откликаться” на внешнее воздействие определенной частоты, имеет место для любых колебательных систем. Для механических колебаний это явление, как правило, нежелательное. Например, толчки, вызванные неровностями дороги, действуя на пружинную подвеску транспортного средства с частотой, близкой к резонансной, могут привести к сильной тряске и другим неприятностям.
С другой стороны, любые радиоприёмные устройства используют это свойство для выделения нужных сигналов из всех других (например, перестраивая радиоприемник или телевизионные каналы вы меняете резонансные частоты определенных колебательных контуров, настраивая их на частоту нужной программы).
1.9.Сложение колебаний одинаковой частоты. Биения
Возможны ситуации, когда в системе присутствуют одновременно два или несколько колебаний. Например, в антенне радиоприёмного устройства присутствует огромное число различных сигналов. Они могут иметь различные частоты и амплитуды, причем реальные сигналы, несущие информацию, в действительности не являются гармоническими, а имеют сложный спектральный состав (т.е. сами состоят из много гармоник). Задача сложения таких колебаний состоящая в том, чтобы найти результирующий сигнал, или, для механических систем, их результирующее движение весьма сложна.
Рассмотрим сначала сложение колебаний одинаковой частоты, имеющих одинаковое направление в пространстве. Пусть имеет два колебания
x1 (t ) = A1 sin(ωt + φ 1 ) , x2 (t ) = A2 sin(ωt + φ 2 ) ,
148
частоты которых совпадают, а амплитуды и фазы могут быть любыми.
Можно показать, что их сумма x = x1 + x2 будет гармоническим колебанием той же частоты, амплитуда и фаза которого зависят от амплитуд и фаз слагаемых.
Дело в том, что колебания одинаковых частот складываются по закону
сложения векторных величин. Представим себе вектор A , который вращается вокруг начала координат с угловой скоростью ω . При этом, если текущее
значение его угла относительно горизонтальной оси x равно
Φ(t ) =ωt +φ ,
где φ - начальное значение, то проекция его на ось x равна
Ax = x (t ) = A cosΦ (t ) = A cos(ωt + φ ) ,
т.е. изменяется по закону гармонических колебаний. (Проекция на ось y - y(t)
пропорциональна синусу того же аргумента). Если имеется два таких вектора, то при сложении, очевидно, их проекции суммируются. Это значит, что нахождение амплитуды результирующего колебания эквивалентно нахождению длины суммарного вектора. (см. рис. 8).
Рис. 8. Сложение векторов A = A1 + A2 , или векторная диаграмма для сложения колебаний.
Она представляет собой диагональ параллелограмма, стороны которого есть складываемые векторы и определяется формулой
|
A 2 = A 2 + A 2 + 2 A A cos(φ |
2 |
− ϕ |
1 |
) . |
(32) |
||||
|
1 |
2 |
1 |
2 |
|
|
|
|
||
Используя её для сложения колебаний, под A1 и |
A2 понимаем амплитуды, а |
|||||||||
под |
φ ,φ 2 - начальные |
фазы. |
Как |
следует |
|
из |
(32), |
результирующая |
||
амплитуда существенно зависит от разности фаз колебаний: максимальное её значение
Amax = A1 + A2
149
будет при разнести фаз равной нулю (или кратной |
2 π |
), такие колебания |
называются синфазными. Минимальное значение |
|
|
Amin = A1 − A2 |
|
|
будет при разности фаз равной π , или (2n + |
1) π . |
Такие колебания |
называются противофазными. |
|
|
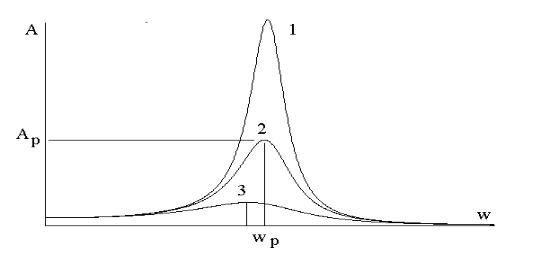
Рис. 9.
Сложение гармонических колебаний. Кривые 1, 2 - складываемые колебания, 3 - их сумма. Верхняя
картинка для разности фаз φ = π / 2 , средняя -
для φ = 0 (синфазные колебания), нижняя - для
φ = π (противофазные колебания).
Сложение колебаний одинаковых частот иллюстрирует рис.9. Заметим, что при равенстве амплитуд противофазные колебания полностью «гасят» друг друга.
Предположим теперь, что частоты складываемых колебаний не равны, но их разность достаточно мала, т.е.
ω = ω 2 − ω 1 << ω 1 |
(33) |
и запишем их в виде |
|
x1 (t) = a cosωt , x2 (t) = a cos(ω + ω )t . |
(34) |
Произведение ω t в силу условия (33) можно рассматривать, |
как разность |
фаз этих колебаний, которая достаточно медленно растет |
со временем. |