Лекция 3
Графы
1
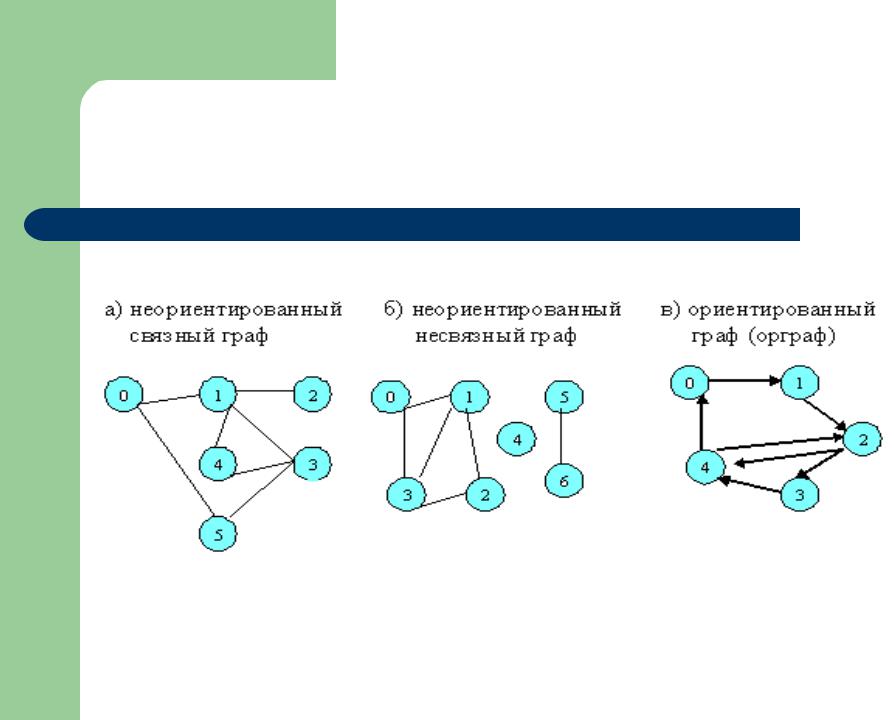
Граф – это множество вершин и соединяющих их ребер.
Примеры графов:
2
Примеры графов:
Схема алгоритма – размеченный орграф, где вершинами являются блоки алгоритма, а дугами
– линии передачи управления.
Система дорог – взвешенный размеченный граф, где вершины – города, а ребра – дороги между городами. Вес ребра – длина дороги, метка вершины – название города. Если дороги односторонние, то граф – ориентированный.
3
Представление графов
1. Последовательность ребер (дуг), перед которой указывается количество вершин графа. Каждое ребро (дуга) задается парой смежных вершин. Такая форма удобна для внешнего представления графа при его вводе.
Пример:
5 - число вершин
0 1
1 2
23
24
3 4
4 0
4 2
4
Если в таком виде хранить граф в памяти, нужно описать два параллельных массива для хранения смежных вершин.
Например:
#define |
NMAX |
10 |
/* макс. число вершин */ |
|||
#define |
RMAX |
100 |
/* макс. число ребер */ |
|||
int |
v1 [RMAX]; |
|
/* массивы смежных */ |
|||
int |
v2 [RMAX]; |
|
/* |
вершин |
*/ |
|
int |
n; |
|
|
/* число вершин графа */ |
||
int |
r; |
|
|
/* число ребер графа |
*/ |
|
5
2. Матрица смежности – |
это квадратная матрица размерности |
||
n*n |
(n – число |
вершин), в которой элемент |
|
ms[i][j] = 1, |
ли есть дуга |
i –> j |
, и = 0 в противном случае. |
Пример матрицы смежности для графа, представленного на рис.
а):
| 0 1 2 3 4 5 |
|
-------------------- |
|
0 | 0 1 0 0 0 1 |
Для неориентированного графа матрица |
1 | 1 0 1 1 1 0 |
смежности симметрична относительно |
2 | 0 1 0 0 0 0 |
главной диагонали. |
3 | 0 1 0 0 1 1 |
|
4 | 0 1 0 1 0 0
5 | 1 0 0 1 0 0
6
Пример ввода неориентированного графа в виде последовательности ребер и формирования матрицы смежности.
#define NMAX 10 /* макс. число вершин */ /* Функция ввода графа */
int VvodGraf ( int ms [NMAX] [NMAX] ) /* ms – матрица смежности */
/* Возвращаемое значение – число вершин графа */
{ int n; |
/* число вершин графа */ |
int i, j; |
/* номера вершин */ |
puts (“\nВведите число вершин графа (<=10)”); scanf (“%d”, &n);
7
/* Обнуление матрицы смежности */ for (i=0; i<n; i++)
for (j=0; j<n; j++) ms[i][j] = 0;
puts (“Введите последовательность ребер, завершив ввод ”); puts (“нажатием Ctrl-Z”);
while (scanf(“%d %d”, &i,&j) !=EOF) ms[i][j] = ms[j][i] = 1;
return n;
}
/* Главная функция */ void main()
{ int g[NMAX][ NMAX] ; /* матрица смежности */
int n; |
/* число вершин графа */ |
… |
|
n = VvodGraf (g); |
/* вызов ф-ции ввода графа */ |
… |
|
} |
|
8
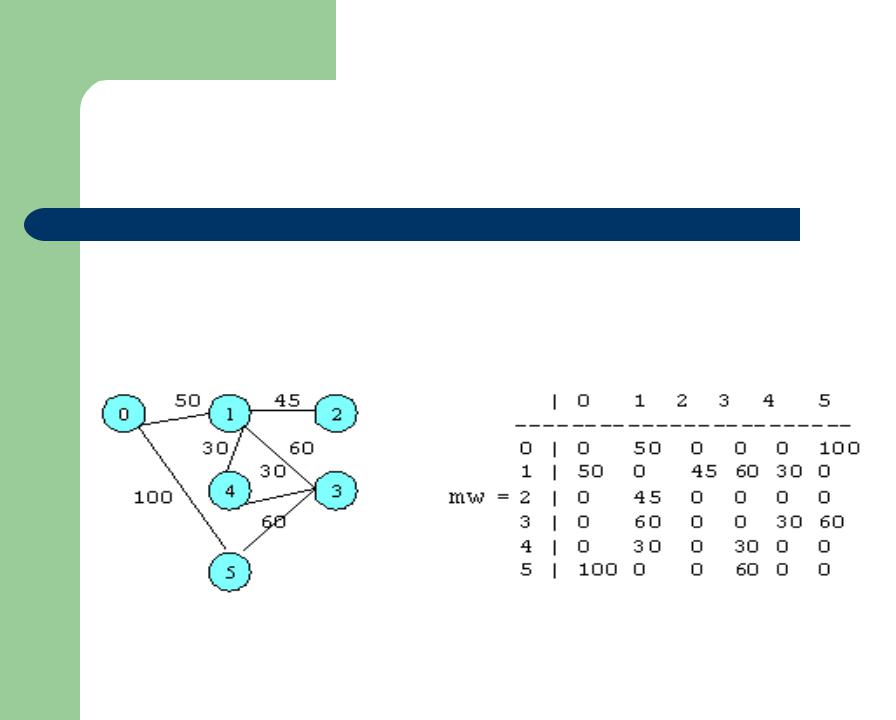
3. Матрица весов – квадратная матрица размерности n*n
(n – число вершин), в которой элемент mw [i][j] = вес дуги i –> j
.
Например, дана система дорог: вершины – города, ребра – дороги. Вес ребра – длина дороги
9
Описание на языке С:
#define NMAX 10 |
/* макс. число вершин */ |
|
int mw[NMAX][ NMAX] ; /* матрица весов |
*/ |
|
int n; |
/* число вершин |
*/ |
10