
- •Электричество и постоянный ток Электронный учебник по физике кгту-кхти. Кафедра физики. Старостина и.А., Кондратьева о.И., Бурдова е.В.
- •Оглавление
- •Электричество и постоянный ток
- •1. Электростатика.
- •1.1. Электрические заряды. Закон сохранения электрического заряда.
- •1.2. Закон Кулона.
- •1. 3. Электростатическое поле и его напряженность.
- •1.4. Графическое изображение электростатических полей
- •1. 5. Принцип суперпозиции электростатических полей.
- •1.6. Электростатическое поле электрического диполя.
- •1.7. Поток вектора напряженности электростатического поля
- •1. 8. Теорема Гаусса для электростатического поля в вакууме.
- •1. 9. Применение теоремы Гаусса для расчета напряженности электростатического поля.
- •1 Рис.1.12. К определению работы перемещения заряда в электростатическом поле. .10. Работа сил электростатического поля при перемещении заряда.
- •1.11. Циркуляция вектора напряженности электростатического поля.
- •1.12. Потенциальная энергия и потенциал электростатического поля.
- •1.13. Связь между потенциалом и напряженностью электростатического поля. Эквипотенциальные поверхности.
- •1.14. Вычисление разности потенциалов по напряженности поля
- •1.15. Диэлектрики в электрическом поле
- •1.15.1. Типы диэлектриков. Поляризация диэлектриков.
- •1.15.2. Вектор поляризации и диэлектрическая восприимчивость диэлектриков
- •1.15.3. Напряженность поля в диэлектрике
- •1.15.4. Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике
- •1.15.5. Сегнетоэлектрики
- •1.15.6. Пьезоэлектрический эффект.
- •1. 16. Проводники в электростатическом поле
- •1. 17. Электрическая емкость уединенного проводника
- •1. 18. Взаимная электроемкость. Конденсаторы
- •1. 19. Энергия заряженного уединенного проводника, конденсатора. Энергия электростатического поля
- •2. Постоянный электрический ток
- •2.1. Электрический ток, сила и плотность тока
- •2.2. Сторонние силы. Электродвижущая сила и напряжение
- •2.3. Закон Ома для участка и полной замкнутой цепи
- •2.4. Сопротивление проводника. Явление сверхпроводимости.
- •2.5. Работа и мощность тока. Закон Джоуля-Ленца.
- •2. 6. Правила Кирхгофа для разветвленных цепей.
- •3. Электрические токи в металлах, вакууме и полупроводниках
- •3.1. Опытные доказательства электронной проводимости металлов.
- •3.2. Основные положения классической теории электропроводности металлов
- •3. 3. Работа выхода электрона из металла. Контактная разность потенциалов.
- •3. 4. Термоэлектрические явления
- •3. 5. Электрический ток в вакуумном диоде
- •3. 6. Собственная и примесная проводимость полупроводников.
- •3.7. Элементы современной квантовой или зонной теории твердых тел.
1.4. Графическое изображение электростатических полей

![]() в различных точках поля является
очень неудобным, так как картина
получается весьма запутанной. Фарадей
предложил более простой и наглядный
метод изображения электростатического
поля с помощьюлиний
напряженностей или
силовых линий.
Силовыми
линиями
называются кривые, касательные к
которым в каждой точке совпадают с
направлением вектора напряженности
поля (рис.1.2). Направление
силовой линии совпадает с направлением
в различных точках поля является
очень неудобным, так как картина
получается весьма запутанной. Фарадей
предложил более простой и наглядный
метод изображения электростатического
поля с помощьюлиний
напряженностей или
силовых линий.
Силовыми
линиями
называются кривые, касательные к
которым в каждой точке совпадают с
направлением вектора напряженности
поля (рис.1.2). Направление
силовой линии совпадает с направлением
![]() .
Силовые линии начинаются на
положительных зарядах и оканчиваются
на отрицательных. Силовые линии не
пересекаются, так как в каждой точке
поля вектор
.
Силовые линии начинаются на
положительных зарядах и оканчиваются
на отрицательных. Силовые линии не
пересекаются, так как в каждой точке
поля вектор![]() имеет лишь одно направление.
Электростатическое поле считается
однородным, если напряженность во всех
его точках одинакова по величине и
направлению. Силовыми линиями такого
поля являются прямые, параллельные
вектору напряженности.
имеет лишь одно направление.
Электростатическое поле считается
однородным, если напряженность во всех
его точках одинакова по величине и
направлению. Силовыми линиями такого
поля являются прямые, параллельные
вектору напряженности.
Силовые линии поля точечных зарядов - радиальные прямые, выходящие из заряда и уходящие в бесконечность, если он положителен (рис.1.3а). Если заряд отрицателен, направление силовых линий оказывается обратным: они начинаются в бесконечности и оканчиваются на заряде -q (рис.1.3б). Поле точечных зарядов обладает центральной симметрией.
Рис.1.3.
Линии напряженности точечных зарядов:
а - положительного, б - отрицательного.

1. 5. Принцип суперпозиции электростатических полей.
Основной
задачей электростатики является
определение величины и направления
вектора напряженности
![]() в каждой точке поля, создаваемого либо
системой неподвижных точечных зарядов,
либо заряженными поверхностями
произвольной формы. Рассмотрим первый
случай, когда поле создано системой
зарядовq1,
q2,...,
qn.
Если в какую-либо точку этого поля
поместить пробный заряд q0,
то на него со стороны зарядов q1,
q2,...,
qn
будут действовать кулоновские силы
в каждой точке поля, создаваемого либо
системой неподвижных точечных зарядов,
либо заряженными поверхностями
произвольной формы. Рассмотрим первый
случай, когда поле создано системой
зарядовq1,
q2,...,
qn.
Если в какую-либо точку этого поля
поместить пробный заряд q0,
то на него со стороны зарядов q1,
q2,...,
qn
будут действовать кулоновские силы
![]() . Согласно принципу независимости
действия сил, рассмотренного в механике,
равнодействующая сила
. Согласно принципу независимости
действия сил, рассмотренного в механике,
равнодействующая сила![]() равна их векторной сумме
равна их векторной сумме
![]() .
.
Используя
формулу напряженности электростатического
поля, левую часть равенства можно
записать:
![]() ,
где
,
где![]() - напряженность результирующего поля,
создаваемого всей системой зарядов в
точке, где расположен пробный зарядq0.
Правую часть равенства соответственно
можно записать
- напряженность результирующего поля,
создаваемого всей системой зарядов в
точке, где расположен пробный зарядq0.
Правую часть равенства соответственно
можно записать![]() ,
где
,
где![]() - напряженность поля, создаваемая
одним зарядомqi.
Равенство примет вид
- напряженность поля, создаваемая
одним зарядомqi.
Равенство примет вид
![]() .
Сокращая наq0,
получим
.
Сокращая наq0,
получим
![]() .
.
Напряженность электростатического поля системы точечных зарядов равна векторной сумме напряженностей полей, создаваемых каждым из этих зарядов в отдельности. В этом заключается принцип независимости действия электростатических полей или принцип суперпозиции (наложения) полей.
Обозначим
через
![]() радиус-вектор, проведенный из точечного
зарядаqi
в исследуемую точку поля. Напряженность
поля в ней от заряда qi
равна
радиус-вектор, проведенный из точечного
зарядаqi
в исследуемую точку поля. Напряженность
поля в ней от заряда qi
равна
 .
Тогда результирующая напряженность
.
Тогда результирующая напряженность![]() ,
создаваемая всей системой зарядов равна
,
создаваемая всей системой зарядов равна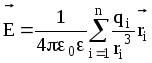 .
Полученная формула применима и для
расчета электростатических полей
заряженных тел произвольной формы
так как любое тело можно разделить на
очень малые части, каждую из которых
можно считать точечным зарядомqi.
Тогда расчет
.
Полученная формула применима и для
расчета электростатических полей
заряженных тел произвольной формы
так как любое тело можно разделить на
очень малые части, каждую из которых
можно считать точечным зарядомqi.
Тогда расчет
![]() в любой точке пространства будет
аналогичен выше приведенному.
в любой точке пространства будет
аналогичен выше приведенному.
