Лекции_1 / Лекция 13

Лекция 13. Ферментативный катализ

Ферменты – катализаторы биологического происхождения, ускоряющие химические реакции, в том числе и процессы, необходимые для жизнедеятельности организмов. Практически все биохимические реакции, происходящие в живых организмах, являются каталитическими, т.е. ускоряются ферментами.

Ферменты отличаются от небиологических катализаторов более высокой активностью и исключительной специфичностью своего действия. Различают два основных типа ерментов:

а) чисто белковой природы;

б) белковой природы, но требующие для проявления каталитической активности соединения с низкомолекулярными органическими веществами – коферментами (в этом случае белковая часть фермента называется аноферментом).

В ряде случаев активность ферментов связана с наличием в их составе металлов, или иных ионов – т.н. оных кофакторов. В белковой молекуле фермента каталитические функции выполняют относительно небольшие участки молекулы, которые получили название активных центров. активный центр фермента представляет собой строго ориентированный в пространстве ансамбль белковых функциональных групп, способный к избирательной химосорбции молекул субстратов с образованием единого комплекса внутри которого происходят химические реакции.

Некоторые ферменты являются комплексами белка, причем РНК также участвуют в катализе. Примером может служить рибосома, сложный ансамбль многих белков и трех типов РНК. В 1986 году было обнаружено, что сама РНК может быть ферментом, что привело к пересмотр основных представлений биохимического катализа. Стало ясно, что фермент не обязательно является белком; другие виды биологических молекул, такие как углеводы, также обладают фрементативной активностью. В настоящее время синтезированы ферменты с каталитической активностью, превышающей природную.

Ферментативная кинетика

Роль ферментов как очень эффективных катализаторов хорошо иллюстрируется на примере разложения пероксида водорода:

2Н₂О₂ → Н₂О + О₂

Эта реакция в чистом водном растворе протекает очень медленно, но ее скорость значительно увеличивается в присутствии различных катализаторов. Увеличение скорости имеет типично первый порядок по концентрации катализатора. Она так­же может иметь приблизительно первый порядк по концентрации Н₂О₂. Однако, в случае разложения высоких концентраций Н₂О₂, ферментом каталазой, реакция имеет нулевой порядок по Н₂О₂. Это характерная черта реакций, катализируемых ферментами.

В табл. 1. приведены кинетические параметры для выражения скорости

Для сравнения в табл. 1 приведены скорости в экстраполированных условиях 1 М Н₂О₂ и 1 М катализатора. Для каталазы приведены максимальные скорости в расче­те на 1 моль активного центра. Как видно из таблицы, скорость некатализируемой реакции соответствует разложению через 11 дней при 25 °С всего лишь 1 % перок­сида, даже тогда, когда частицы пыли, трудно удаляемые из раствора, вероятно, «катализируют» реакцию. Неорганические катализаторы, такие как соли железа или галоидоводороды, увеличивают скорость разложения Н₂О₂ на 4—5 порядков в рас­чете на моль катализатора. Фермент каталаза, существующий в крови и различных тканях (печени, почках, селезенке и т. д.), увеличивает скорость более чем в 10¹⁵ раз по сравнению с некатализируемой реакцией! Оцените скорости этой ферментатив­ной реакции, представив, что при максимальной скорости каждая молекула ката­лазы может разлагать более чем 10 миллионов молекул Н₂О₂ в секунду!

Таблица 8.1. Каталаза и разложение Н₂О₂: сравнение скоростей и энергий активации при 25 °С¹

Каталаза является гемопротеином, содержащим в активном центре феррипро-топорфирин (гематин) в качестве простетической группы (гематин осуществляет каталитическую функцию). Гематин можно отделить от белка. В растворе гематин обладает каталитической активностью по отношению к разложению Н₂О₂ на 2 по­рядка большей, чем неорганические катализаторы, но все же более чем в миллион раз меньшей, чем каталаза.

Термодинамика разложения пероксида водорода также зависит от функции ка­тализатора. Реакция

Н₂О₂ (aq) → Н₂О (ж) + 1/2О₂ (г)

является экзоэргической, ΔG⁰₂₉₈ = -103.10 кДж моль^-1, причем основной вклад в изменение свободной энергии дает изменение энтальпии, ΔH⁰₂₉₈ = -94,64 кДж моль^-1. Таким образом, при соответствующем пути реакции разложение Н₂О₂ будет идти прак­тически до конца. Низкая скорость некатализируемой реакции связана с высоким барьером активации. Экспериментальная энергия активации равна 71 кДж моль^-1 (табл. 1). Используя наблюдаемые значения скорости некаталитического разло­жения, v < 4 ∙ 10^-8 М с^-1, мы можем рассчитать верхний предел предсэспоненци-ального множителя Аррениуса А < 1 ∙ 10⁵ с^-1, считая, что «некатализируемая» реак­ция является реакцией первого порядка. Хотя предэкспоненциальный множитель А значительно меньше наблюдаемых в других реакциях первого порядка, тем не менее, ясно, что энергия активации вносит больший вклад в энергетический барь­ер реакции. Ход реакции представлен на рис. 1.

Рис. 1. Роль каталазы в снижении энер­гии активации разложения Н₂О₂.

Энергия активации реакции Н₂О₂, катализируемой Fe²⁺/Fe³⁺ или НВк, составля­ет две трети по сравнению с реакцией без катализатора. В присутствии каталазы энергия активации составляет всего 8 кДж моль^-1, а предэкспоненциальный мно­житель Аррениуса — 1.6 ∙ 10⁸ М^-1 с^-1. По-видимому, фермент (и в меньшей степени другие катализаторы) способствует ускорению реакции за счет пути со значитель­ной меньшей энергией активации (см. рис. 1). Энтропийный барьер также сни­жен (отсюда большой А множитель), но его влияние на скорость реакции менее выражено при комнатной температуре. Заметим, что снижение величины барьера прямой реакции подразумевает также снижение энергии активации и обратной ре­акции. В данном случае обратная реакция в значительной мере эндоэргическая; даже при понижении величины энергетического барьера прямой реакции обратная реакция остается очень медленной. Однако, для большинства биохими­ческих реакций, которые мы будем рассматривать, изменение стандар­тной свободной энергии суммарной реакции близко к нулю. В этих слу­чаях и прямая и обратная реакции в присутствии фермента протекают с большими скоростями.

Типичным для реакции с одним субстратом, катализируемой ферментом, явля­ется то, что при низких концентрациях субстрата она имеет первый порядок по субстрату, а затем при высоких концентрациях порядок становится нулевым. Это означает, что реакция достигает максимальной скорости по мере роста концентра­ции субстрата при постоянной концентрации фермента. Каталитическая констан­та или число оборотов определяется как максимальная скорость (М с^-1), деленная на концентрацию активных центров фермента (М). Ее единицей является с^-1. Кон­центрация активных центров используется вместо концентрации фермента для удоб­ства сравнения с ферментами, имеющими более одного активного центра. Каталаза имеет в молекуле четыре активных центра.

Было бы ошибочно считать активность каталазы типичной для реакций, ката­лизируемых ферментами (табл. 2). Каталаза является самым быстрым ферментом (по величине активности — на несколько порядков выше других). Более типичные значения каталитических констант ферментов — 10³ с^-1, а многие значения — даже в 10 раз меньше. Однако это не говорит о том, что другие ферменты плохие ката­лизаторы. Фермент фумараза катализирует гидратацию фумарата с образованием L-малата с каталитической константой 2,5 ∙ 10³ с^-1 при 25 °С:

Константы скорости гидролиза 1 М фумарата кислотой (1 М) или основанием (1 М) — примерно около 10^-8с^-1. Этот «простой» фермент имеет преимущество в 10¹¹ раз.

Таблица 2. Каталитические константы некоторых ферментов

Кинетика Михаэлиса—Ментен

Поскольку ферменты являются необычайно эффективными катализаторами, они способны проявлять свое влияние при исключительно низких концентрациях, обыч­но от 10^-10 до 10^-8 М. При этом уровне концентрации трудно производить прямые измерения того, что делает сам фермент, особенно если учесть, что ферменты в находятся в сложном клеточном соке. Поэтому энзимология началась с изучения кинетики исчезновения субстрата или образования продукта, поскольку их кон­центрации обычно составляют от 10^-6 до 10^-3 М. В ранних работах были сделаны следующие обобщения о ферментативных реакциях:

1. Скорость превращения субстрата возрастает линейно с увеличением концен­трации фермента (рис. 2).

2. Для низких значений концент­рации субстрата [S] при фиксирован­ ной концентрации фермента скорость линейно зависит от [S] (рис. 3).

3. При высоких концентрациях субстрата скорости ферментативных реакций достигают максимума или Относительное количество фермента уровня насыщения (рис. 8.3). При низких концентрациях

v₀ = k[S], (1)

где v₀ — начальная скорость.

Рис. 2. Увеличение концентрации про­дукта во времени для четырех различных количеств фермента.

Рис. 3. Начальная скорость v₀ ре­акции, катализируемой ферментом как функция концентрации суб­страта [S] для фиксированного ко­личества фермента.

При высоких концентрациях

v₀ = V_max (максимальная скорость) (2)

Такое поведение возможно, если фермент образует комплекс с субстратом. При высоких концентрациях субстрата практически весь фермент связан в фермент-субстратный комплекс. При этих условиях фермент работает в полную силу, что определяется с помощью его каталитической константы:

каталитическая константа = k_кат = V_max /[Е]₀ (3)

где [Е]₀ — общая концентрация ферментных центров. При низкой концентрации субстрата фермент ненасыщен и его оборот частично лимитирован доступностью субстрата.

Михаэлис и Ментен представили кинетическую формулировку этих идей, а Бриггс и Холдейн (1925) усовершенствовали их теорию. В простейшем виде фер­мент и субстрат обратимо образуют комплекс, при последующей диссоциации ко­торого образуются продукты и регенерируется свободный фермент:

(4)

(5)

Поскольку второй этап также может быть обратимым, этот механизм строго приме­ним только к начальным стадиям реакции, до того, как концентрация продукта сильно возрастет. При этих условиях

(6)

Используем стационарное приближение

Тогда

(7)

[E] и [S] соответствуют концентрациям свободного фермента и субстрата; однако, их трудно измерить, поэтому мы перепишем уравнение в терминах измеряемых общих концентраций фермента [Е]₀ и субстрата [S]₀:

(8)

Поскольку концентрация фермент-субстратного комплекса обычно мала по срав­нению с концентрацией субстрата, можно приравнять общую концентрацию суб­страта к его свободной концентрации. Подставив [Е] из уравнения (8) в уравне­ние (7) и перегруппировав члены, мы получим

(9)

Подстановка в уравнение (6) дает

(10)

где K_M = (k_-1 + k₂)/k₁ — константа Михаэлиса для фермент-субстратного комплек­са, a V_max = k₂[Е]₀. Уравнение (10) называется уравнением Михаэлиса—Ментен. Лимитирующие условия, приведенные в уравнениях (1) и (2), непосредственно следуют из уравнения (10). При низких концентрациях субстрата, когда K_M/[S] >> 1, уравнение (10) дает

(1)

где k = V_max/K_M является постоянной при фиксированной общей концентрации фермента [Е]_о. При высоких концентрациях субстрата, когда K_M/[S] << 1, уравнение (10) сокращается до

v₀ = V_max (максимальная скорость) (2)

(3)

В случае, когда концентрация субстрата [S] равна K_M уравнение (10) дает

v₀ = V_max

Таким образом, константа Михаэлиса равна концентрации субстрата, соответству­ющей половине максимальной скорости фермента. Графически это показано на рис. 3. Низкие значения К_м означают, что фермент прочно связывает субстрат, и его небольшие концентрации достаточны для насыщения фермента и достижения его максимальной каталитической эффективности.

В принципе, реакции, катализируемые ферментами, обратимы, но мы должны учитывать вклад обратной реакции только при значительных количествах продук­та. Использование начальных стадий реакции позволяет избежать этих трудностей. Если обратная реакция не играет роли (например, если положение равновесия зна­чительно сдвинуто в сторону образования продуктов), можно использовать интег­ральную форму уравнения Михаэлиса—Ментен, которая дает зависимость концен­трации субстрата от времени. Используя запись уравнения (8.10) как -d[S]/dt, мы получим

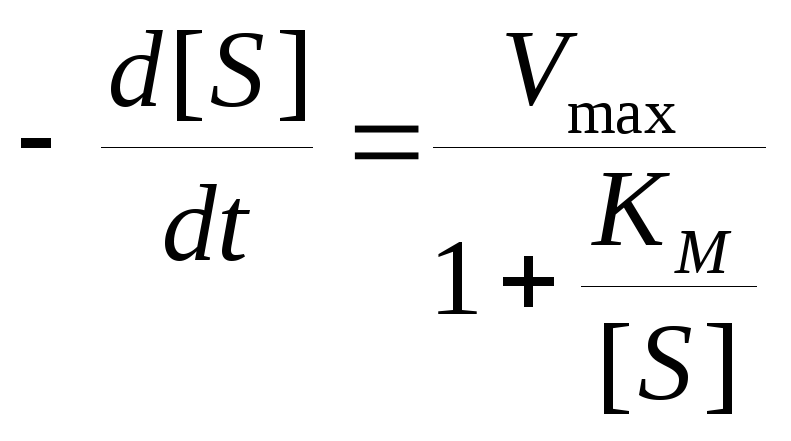(10)

Разделив переменные в этом уравнении, мы получим выражение

которое можно проинтегрировать с учетом того, что [S] = [S]₀ в момент времени t = 0.

Без знания К_м невозможно построить график зависимости функции [S] от времени. Однако, с использованием компьютера получение точных значений К_м и V_max из имеющихся данных становится рутинной операцией.

Очень немногие ферменты работают по простому механизму с одним фермент-субстратным комплексом. Однако даже в наиболее сложных ситуациях кинетичес­кие уравнения имеют вид, представленный уравнением (10).

1 Скорость рассчитана для 1 М Н₂О₂ и 1 М катализатора (за исключением каталазы). В случае каталазы максимальная скорость приведена для 1 М концентрации активных центров. Эта скорость численно равна каталитической константе каталазы. ТЕТА — триэтилентетрамин. Обсуждение механизма реакции и ссылки на более раннюю литературу см. J.H. Wang, 1955, J. Am. Chem. Soc. 77:4715.