8256

Учитывая сказанное, при построении критерия проверки статистической гипотезы необходимо сначала задаться допустимым уровнем риска на совершение ошибки I рода, как наиболее значимой, а затем минимизировать ошибки II рода.

3. Построение критерия проверки гипотезы

Пусть необходимо проверить простую гипотезу Н0 = {X ↔ f X (x, θ)} , состоящую в предположении о виде функции плотности распределения случайной величины Х с вполне определенными параметрами q . Построим критерий, однозначно принимающий или отвергающий проверяемую гипотезу по

каждая из которых противоречит основной. Альтернативные гипотезы необходимы при построении критерия проверки основной гипотезы для ее сравнения с имеющимися альтернативами (все познается в сравнении с чем-то).

Критерий проверки гипотезы состоит из двух составляющих:

Во-первых, в качестве критерия принимается некоторая случайная величина К , с известным распределением при условии справедливости основной

Во-вторых, строится решающее правило для критерия проверки, согласно которому гипотеза будет приниматься или отвергаться. Для этого, назовем

Точки значения критерия К , где критическая область критерия проверки Кkr отделяется от области принятия гипотезы, называются критическими точками критерия kkr . Как построить критическую область критерия или, что равно-

сильно, как найти критические точки критерия? Ниже рассмотрим ответ на этот вопрос.

Зададимся вероятностью α ошибки I-го рода, как наиболее значимой. Исключить такую ошибку при проверке гипотезы невозможно ( a ¹ 0 ), но в вероятностных задачах это не является трагедией. На практике обычно эту ве-

80

роятность задают достаточно малой величиной α = 0,05 ; α = 0,025 ; α = 0,005 и называют уровнем значимости критерия.

Если из условия

P(k K kr ) = ∫ f K (k / H 0 )dx = α

Kkr

можно определить критические точки kkr однозначно, то задача построения

критической области критерия решена. В противном случае, когда еще остается свобода выбора критических точек, рассмотрим влияние альтернативных гипотез. Поскольку величина:

∫ f K(k / H j )dx = 1 − β j есть вероятность правильного отбрасывания H 0 при ус-

Kkr

ловии справедливости H j , то ее называют мощностью критерия по отноше-

нию к альтернативной гипотезе H j . Поэтому при заданном уровне значимости

α , критическую область критерия нужно строить так, чтобы мощность критерия была максимальной, а именно:

(1− β j ) max , для наиболее мощного критерия (НМК) относительно гипотезы H j , максимизация проводится по параметрам сложной гипотезы;

min (1− β j ) max , для равномерно наиболее мощного критерия (РНМК), в случае наличия нескольких сложных гипотез.

Величина β j - есть вероятность принять неверную гипотезу H 0 при условии справедливости альтернативной гипотезы H j .

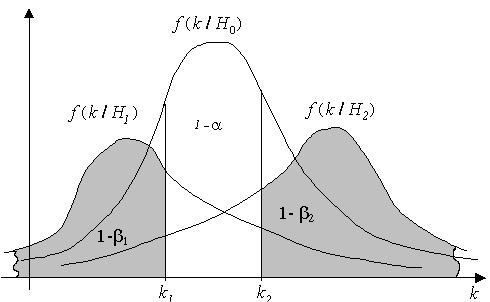
Рис. 13.1. Двухсторонняя критическая область критерия

Кkr = {k > k2 , k < k1} при наличии двух альтернативных гипотез H1 , Н2 . 81

На рис. 13.1 приведена графическая интерпретация алгоритма построения критической области одномерного критерия. Видим, что структура критической области, зависит от наличия альтернативных гипотез и их “ расположения” относительно основной.

Лекция № 14

Примеры построения критериев проверки гипотез

истинного (гипотетического) математического ожидания а некоторой величине a0 . Основная гипотеза тем самым будет следующей H 0 = {a = a0 } . В ка-

честве критерия K возьмем случайную величину имеющую, при справедливости основной гипотезы, распределение Стьюдента с n-1 степенями свободы:

K = xB − a0 = tn−1 S / n

Задаваясь уровнем значимости α для проверяемой гипотезы H 0 , будем строить критическую область K kr в зависимости от вида единственной конкурирующей (альтернативной) гипотезы H1 в следующих случаях:

82

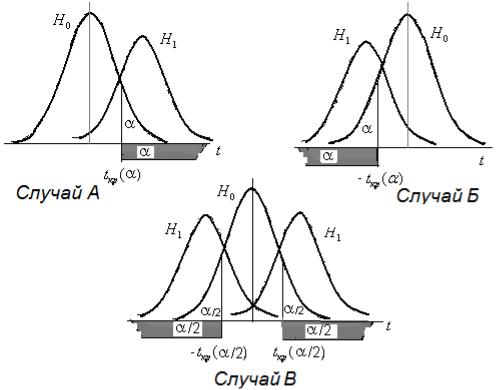
Случай А: H1 = {a > a0 } . В этом случае, при справедливости конкури-

рующей гипотезы ожидаем сдвиг вероятных значений критерия K в большую сторону (рис.14.1), поэтому критическая область критерия будет правосторон-

бой правостороннюю квантиль распределения случайной величины Стьюдента и приводится таблицей в приложении 3.

Рис. 14.1 Критические области гипотезы H 0 = {a = a0 } .

Случай Б: H1 = {a < a0 }. В этом случае, критическая область критерия будет левосторонней K kr = {k < kkr } , а значения критерия отрицательными (рис.14.1). Критическая точка kkr определяется из уравнения P(k < kkr ) = a ,

P(k < kkr1 ) + P(k > kkr 2 ) = a . Доказано [9], что при условии P(k < kkr1 ) = a / 2 и P(k > kkr 2 ) = a / 2 мощность критерия (1 − β) по отношению к конкурирую-

83

щей гипотезе Н1 будет максимальной. Тогда из этих уравнений критические точки находятся однозначно и представляют собой двухстороннюю квантиль распределения случайной величины Стьюдента:

kkr1 = −tkr (α / 2; n −1) , kkr 2 = tkr (α / 2; n −1) .

Рассмотрим числовой пример: Пусть по выборке объема n=16 получена оценка математического ожидания наблюдаемой нормальной случайной вели-

чины хВ =10,2 и оценка среднеквадратического отклонения S = 6,5 . Поскольку, каждая оценка есть величина случайная (получена по конкретной случайной выборке), то проверим гипотезу о том, что истинное математиче-

гается, т.е. отличие наблюдаемого значения математического ожидания от гипотетического значительны.

1.2. H 0 = {σ2 = σ02 } Проверим теперь гипотезу о том, что истинная (гипотетическая) дисперсия случайной величины равна s02 . Проверяемая гипотеза H0 = {σ2 = σ02} В качестве критерия возьмем одномерную случайную величину K , имеющую распределение «хи-квадрат» с n-1 степенями свободы:

Задаваясь уровнем значимости α для проверяемой гипотезы H 0 , будем стро-

ить критическую область K kr в зависимости от вида единственной конкурирующей (альтернативной) гипотезы H1 в следующих случаях (рис.14.2):

Случай А: H1 = {σ2 > σ02 } . В этом случае, при справедливости конкури-

рующей гипотезы ожидаем сдвиг наиболее вероятных значений критерия K в большую сторону, поэтому критическая область будет правосторонней.

84

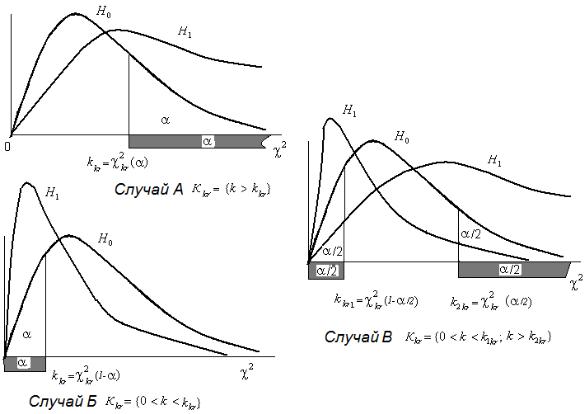
Рис. 14.2 Критические области гипотезы H 0 = {σ2 = σ02 }.

Критическая точка kkr здесь однозначно определяется согласно общему под-

ходу к построению критических областей критерия из условия равенства вероятности ошибки I-рода заданному уровню значимости α :

∞

P(k > kkr ) = ∫ χ2 (k; n − 1)dk = α .

kkr

Решение этого уравнения kkr = χ2kr (α; n −1) находятся однозначно, и

представляет собой правостороннюю квантиль «хи-квадрат» распределения случайной величины и приводится в приложении 4.

Случай Б: H1 = {σ2 < σ02 } . В этом случае критическая область критерия

будет левосторонней, а критическая точка однозначно определяется из уравнения :

Левосторонняя критическая точка может быть легко выражена через функцию для правосторонней критической точки. Действительно, т.к.

P(k < k kr ) + P(k > k kr ) = 1 , то P(k > kkr ) = 1− α и тогда решение для левосторонней точки будет следующим kkr = χ2kr (1 − α; n −1) .

85

максимальной, тогда из этих двух условий критические точки находятся однозначно:

kkr1 = χ2kr (1 − α / 2; n −1) ; kkr 2 = χ2kr (α / 2; n −1) .

Рассмотрим числовой пример: Пусть по выборке объема n=15 получена оценка дисперсии наблюдаемой нормальной случайной величины S 2 = 40,25 или оценка среднеквадратического отклоненияS = 6,5 . Поскольку, каждая оценка есть величина случайная (получена по конкретной случайной выборке), то проверим гипотезу о том, что истинная дисперсия наблюдаемой величины

потеза принимается, т.е. отличия наблюдаемого значения дисперсии от гипотетического незначительны. Если бы, такая оценка дисперсии была получена по выборке меньшего объема n=7, то

kkr1 = χ2kr (1 − 0,025;6) = 14,4; kkr 2 = χ2kr (0,025;6) = 1,24.

тогда наблюдаемое значение критерия k nab = 15,653 попадает в критическую область и тогда проверяемая гипотеза отвергается.

Отметим, что при проверке гипотез H 0 = {a = хВ } и H 0 = {s2 = S 2 } при уровне значимости α будут построены двухсторонние критические области такими, что область принятия гипотез Kkr совпадет с доверительными интервалами, построенными с надежностью γ = 1− α .

86

2. Критерий согласия Пирсона

Критериями согласия называются критерии проверки статистических гипотез о виде распределения случайной величины. Проверяемая гипотеза имеет вид:

H0 = {X ~ f Х (x, θ1, θ2 ,...θr ) ,

где θ1 , θ2 ,...θr - принятые в гипотезе параметры распределения. Пирсон предложил и обосновал следующий критерий проверки гипотезы H 0 по отношению к единственной альтернативной противоположной гипотезе

H1 = H 0 .

Пусть по полученной выборке хВ = {xi , i = 1, n} = {x1 , x2 ,...xn } построена гистограмма наблюдаемых частот H Xn = {hj , n j ; j = 1, m}. Построим, так же теоретические частоты nTj для интервалов hj при условии справедливости проверяемой гипотезы H 0 . Теоретические частоты вычисляют-

при достаточно большом объеме выборки имеет «хи-квадрат» распределение с m − r −1 степенями свободы и может быть использована в качестве критерия для проверки гипотезы H 0 . Задаваясь уровнем значимости α

можем однозначно определить правостороннюю критическую область критерия из уравнения

P(χ2 > χ2kr ) = α

Его решение представляет собой правостороннюю квантиль «хи-квадрат» распределения χ 2kr = χ 2kr (α, m − r − 1) и приведено в приложении 4.

87

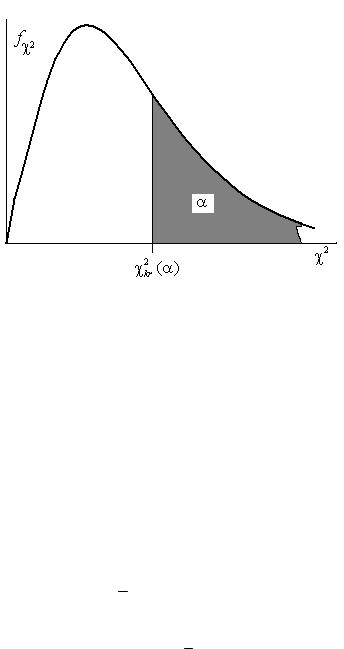
Рис. 14.3. Критическая область критерия Пирсона.

Определив, таким образом, критическую точку χ2kr , сравним ее с наблюдаемым значением χ2nab получим правило проверки гипотезы:

(отклонения частот значительны).

Числовой пример: Проверим гипотезу о нормальном распределении полуденных температур месяца мая для выборки, приведенной в лекции

10, при уровне значимости гипотезы α = 0,05 . Вычислив выборочные ха-

рактеристики хВ = 14,6 и S = 7,5 , примем их за оценки параметров нормального распределения. Таким образам проверяемая гипотеза такова:

H0 = {X = N (a, σ); а = хВ ; σ = S}.

Учитывая, что для нормальной случайной величины Х функция

(приложение 2), то для теоретических частот получим формулу:

валов h j разбиения данных в гистограмме. Все результаты приведем в таблице 8 и на рис.14.4.

Таблица 8.

88

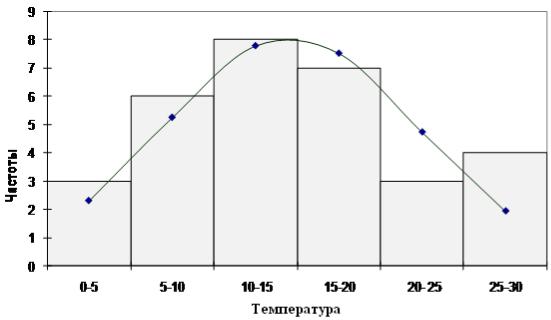Рис. 14.4. Гистограмма наблюдаемых частот и кривая теоретических частот.

По заданному уровню значимости проверяемой гипотезы H 0 определим критическую точку распределения «хи-квадрат» используя приложе-

оснований ее отвергнуть), т.к. отклонения частот незначительны.

Примеры заданий для проверки различных статистических гипотез для самостоятельной работы студентов приводятся в [12].

89