3.9. Характеристические параметры четырехполюсника

Для несимметричных четырехполюсников можно подобрать такую пару сопротивлений и, для которых соблюдаются следующие условия:

1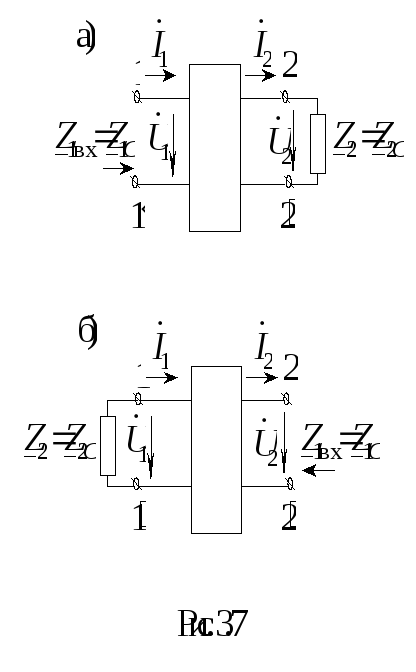. Входное со­противление со сто­роны выводов 1–1, если к вы­водам 2–2подклю­чено со­противление(рис. 3.7, а).

2. Входное со­против­ление со сто­роны выводов 2–2, если к вы­водам 1–1подклю­чено сопротивление(рис. 3.7, б).

и называютхарактеристическими сопротивлениями (характеристическими параметрами) четырехполюсника.

Выразим ичерезА–параметры. Для этого воспользуемся уравнениями (3.9) и (3.11):

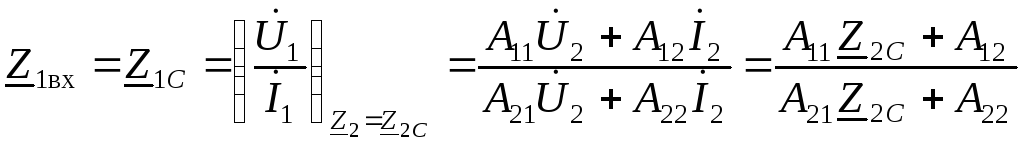. (3.23)

При выводе этого соотношения числитель и знаменатель дроби разделили на и учли, что при.

Из уравнений (3.11) следует, что

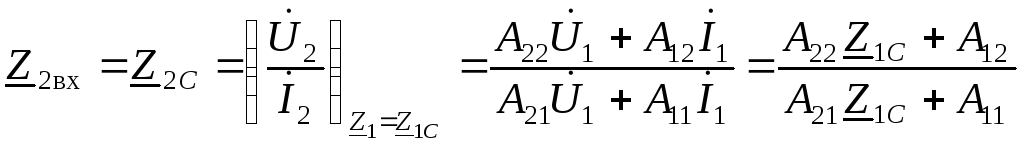. (3.24)

При выводе соотношения (3.24) числитель и знаменатель дроби разделили на и учли, что при принятых условиях.

Решая совместно уравнения (3.23) и (3.24) относительно и(два уравнения с двумя неизвестными), получим:

(3.25)

. (3.26)

Учитывая (3.12) – (3.15), получим

. (3.27)

Третьим характеристическим параметром четырехполюсника является постоянная передачи (или мера передачи), которая характеризует четырехполюсник как элемент, через который передается мощность, и в общем случае представляет собой комплексное число

, (3.28)

где –постоянная ослабления,–постоянная фазы.

Физический смысл величин ипоясним ниже.

Постоянная передачи должна удовлетворять условиям

, (3.29)

. (3.30)

Эти выражения не противоречат соотношению (3.10), т.к.

.

, ,называютвторичными параметрами четырехполюсника. Эти величины независимы друг от друга и являются функциями параметров четырехполюсника.

3.10. Уравнения четырехполюсника в гиперболических функциях

Выразим с помощью характеристических параметров соотношения между выражениями и токами на входе и выходе четырехполюсника. С этой целью разделим и умножим (3.25) на (3.26):

, (3.31)

. (3.32)

Умножим и разделим (3.29) на (3.31):

, (3.33)

. (3.34)

Умножим и разделим (3.30) на (3.32):

, (3.35)

. (3.36)

Таким образом, с помощью уравнений (3.33) – (3.36) можно выразить А–параметры через характеристические параметры четырехполюсника. Для этого (3.33) – (3.36) подставим в (3.9), тогда

, (3.37)

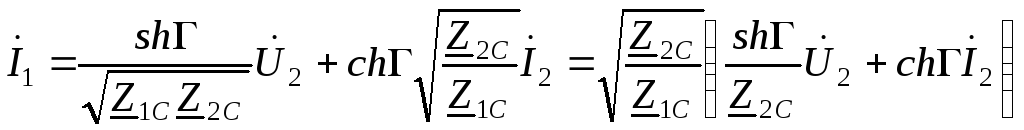. (3.38)

Получили уравнения четырехполюсника, в которых ,,,связаны друг с другом с помощью трех независимых характеристических параметров. Поскольку в эти соотношения входят гиперболические функции, то они называютсяуравнениями четырехполюсника в гиперболических функциях.

3.11. Режим согласованной нагрузки четырехполюсника

Подключим к выходным выводам четырехполюсника , тогда. Это соответствует режиму согласованной нагрузки. Согласованный режим – это режим передачи максимальной мощности. В этом случае. Вынесем в (3.37), а в (3.38)за скобки, тогда

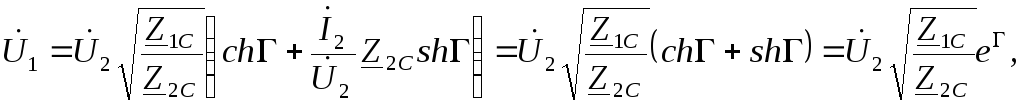(3.39)

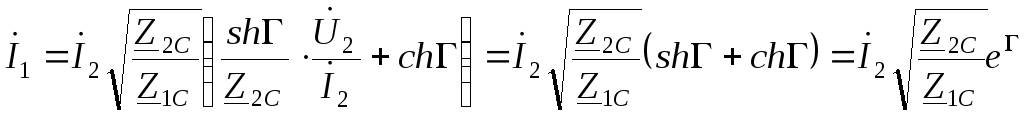. (3.40)

Уравнения (3.39), (3.40) называют уравнениями четырехполюсника для согласованного режима. Найдем произведение входного тока и напряжения

.

Отсюда

. (3.41)

В случае ,,,

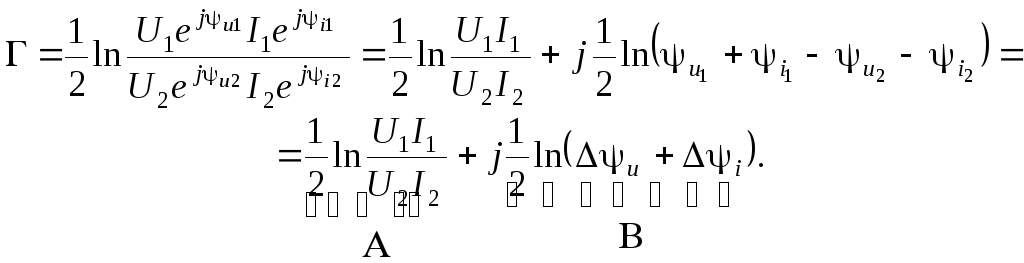(3.42)

Приведенные соотношения позволяют пояснить физический смысл и:–постоянная ослабления (коэффициент затухания), учитывает изменение полной мощности сигнала при прохождении через четырехполюсник;–постоянная фазы (коэффициент фазы), показывает изменение фазы напряжения и тока при прохождении сигнала от первичных выводов к вторичным.

Значения иможно определить из уравнений

. (3.43)

В симметричных четырехполюсниках , тогда на основании (3.25)

Связь между напряжениями и токами на входе и выходе четырехполюсника можно выразить с помощью двух характеристических сопротивлений и меры передачи. На основании (3.37) и (3.38) для симметричных четырехполюсников

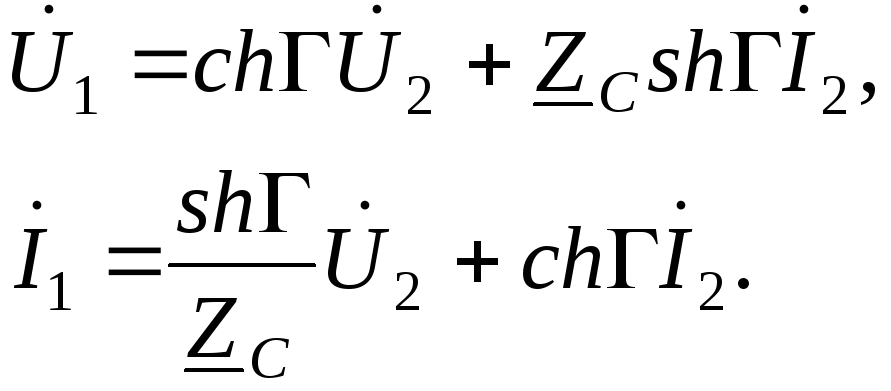(3.44)

Если симметричный четырехполюсник нагрузить на , то согласно (3.39), (3.40)

. (3.45)

Для симметричного четырехполюсника характеристическое сопротивление называютповторным. Это объясняется тем, что привходное сопротивление со стороны входных выводов тоже будет равно, следовательно, (3.45) можно представить следующим образом:

,

отсюда

. (3.46)

Из этих соотношений еще более четко просматривается физический смысл постоянной ослабления и фазы.

Единицы измерения постоянной ослабления и фазы

Постоянная ослабления измеряется внеперах. 1 непер соответствует уменьшению модуля напряжения или тока вe раз при прохождении тока от входных выводов к выходным в симметричном четырехполюснике, нагруженном на. Постоянная фазыизмеряется врадианах илиградусах. Применяются и другие единицы измерения ослабления –белы идецибелы. Постоянная в белах определяется по формуле

,

где S₁,S₂– полные мощности соответственно на входе и выходе четырехполюсника.

Для симметричного согласованного четырехполюсника

.

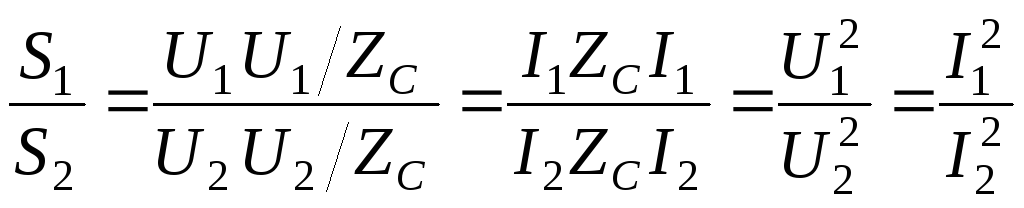В этом случае постоянная ослабления (в белах)

.

В децибелах ослабление

.