3.6. Эквивалентные схемы замещения четырехполюсника

Л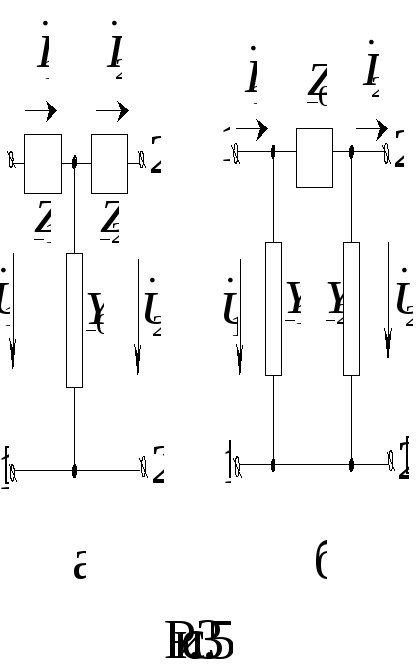юбой четырехполюсник можно свести к сопротивлениям или проводимостям, соединенным по Т– или П–образной схеме (рис. 3.5). Эквивалентной схемой замещения реального четырехполюсника называется простейший трехэлементный четырехполюсник (Т– или П–образный), имеющий такие жеилиA–параметры, как и заданный четырехполюсник.

Три сопротивления Т– или П–схем должны быть рассчитаны с учетом того, что схема замещения должна обладать такими же А-параметрами, какими обладает заменяемый ей четырехполюсник.

Выразим иТ–образной схемы через,, используя уравнения, составленные по законам Кирхгофа:

(3.18)

Подставляя в выражение для определенияи группируя однородные члены, получим

.

С другой стороны для данной схемы справедлива общая запись уравнений четырехполюсника в А–параметрах:

.

Приравняв коэффициенты при и, получимА–параметры как функции параметров Т-образной схемы замещения:

(3.19)

Проведя аналогичные действия, можно получить подобные соотношения для П–образной схемы четырехполюсника:

(3.20)

Два четырехполюсника эквивалентны, если у них равны А–параметры. Это следует из уравнений (3.9). Следовательно, если известныА–параметры какого-то четырехполюсника, то его можно заменить на эквивалентную ему Т– или П–образную схемы замещения, если определить параметры этих схем замещения в выражениях (3.19) и (3.20). При этом для Т–образной схемы замещения

. (3.21)

Параметры элементов П–образной схемы замещения

. (3.22)

3.7. Симметричный четырехполюсник

Встречаются такие электрические схемы, у которых наблюдается симметрия параметров относительно входных и выходных выводов. В эквивалентных схемах замещения это приводит к следующему: для Т–схемы ; для П–схемы.

Тогда для Т–схемы

,

для П–схемы

.

Следовательно, для симметричного четырехполюсника . Таким образом, симметричный четырехполюсник характеризуется двумя независимыми параметрами.

3.8. Родственные четырехполюсники

Расчет коэффициентов с помощью формул (3.16 – 3.17) дает два решения, так как при извлечении квадратного корня А₁₁ может принять как положительные, так и отрицательные значения. В результате, помимо матрицы [А], получаемой также с помощью соотношений (3.19), появляется дополнительное решение в виде новой матрицы, каждый элемент которой имеет противоположный знак.

Наличие двух решений традиционно объясняют тем, что коэффициенты A_ij зависят не только от того, какова структура и состав четырехполюсника, но также и от положительных направлений напряжений и токов на входе и выходе. Последнее обстоятельство не может быть учтено ни расчетом, ни экспериментальным определением сопротивлений в режимах холостого хода и короткого замыкания. Представляется, что возникновение двух решений может также иметь иное объяснение. Изменение полярности выходного тока и напряжения, схемно реализуемое в виде перекрещивания выходных зажимов, образует новый четырехполюсник, характеризующийся своей схемой замещения и матрицей [А]. Таким образом, возникает понятие родственных четырехполюсников, одновременно удовлетворяющих одним и тем же значениям входных сопротивлений Z_1х, Z_2х, Z_1k, Z_2k. И в этом отношении оба таких четырехполюсника равноправны. У всех коэффициентов матрицы [А]₍₂₎ родственного четырехполюсника знаки меняются на противоположные по отношению к коэффициентам матрицы [А]₍₁₎.

С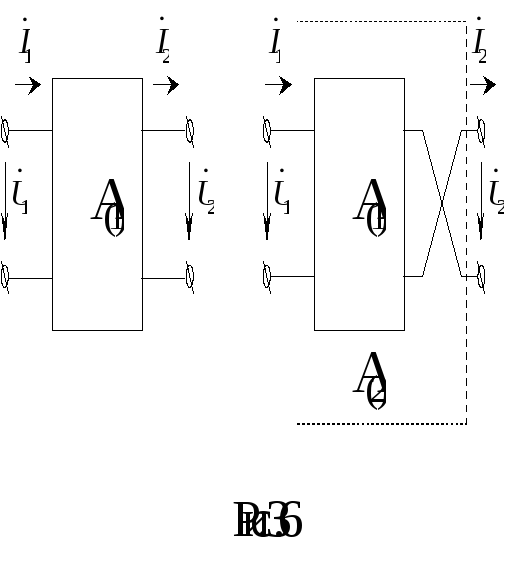хемы замещения родственных четырехполюсников различны, а соответствие с точки зрения передающих свойств можно проиллюстрировать с помощью рисунка 3.6.

Следует отметить, что схемная реализация родственных четырехполюсников в ряде случаев невозможна, так как в результате расчета параметров схем замещения могут быть получены отрицательные значения активных сопротивлений.