
8115
.pdf
В то же время по отношению к напряжениям σ2 и σ3, ребро элемента, параллельное σ1,
является поперечным размером, а потому под действием напряжений σ2 и σ3 элемент в на-
правлении σ1 испытывает относительные укорочения, равные:
ε |
= -ν×ε |
22 |
= -ν |
σ2 |
, ε = -ν×ε |
33 |
= -ν |
σ3 |
. |
(2.7) |
|
|
|||||||||
12 |
|
|
Е |
13 |
|
Е |
|
|||
|
|
|
|
|
|
|
|
|||
Здесь ν = ε' – коэффициент поперечной деформации, называемый коэффициентом Пуассо-
ε
на; ε' – относительная поперечная деформация; ε – относительная продольная деформация.
Таким образом, полная относительная деформация элемента в направлении напряжения
σ1 выразится суммой:
ε1 = ε11 + ε12 + ε13 |
= |
σ1 |
- ν |
σ2 |
- ν |
σ3 |
= |
1 |
[σ1 - ν(σ2 + σ |
3 )] . |
(2.8) |
Е |
Е |
Е |
|
||||||||
|
|
|
|
|
Е |
|
|
||||
Подобные же выражения получим и для деформаций в двух других направлениях. В ре-
зультате имеем:
ε = |
1 |
[σ − ν(σ |
|
+ σ |
|
)] |
|
|
|||
|
|
2 |
3 |
|
|
||||||
1 |
|
Е |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
ε2 |
= |
|
|
|
[σ2 − ν(σ1 |
+ σ3 )] . |
(2.9) |
||||
|
|
|
|||||||||
|
|
|
Е |
|
|
|
|
|
|
|
|
ε3 = 1 [σ3 − ν(σ1 + σ2 )]
Касательные напряжения не вызывают удлинений ребер выделенного параллелепипеда, а
вызывают лишь изменения прямых углов между его гранями. Закон Гука в общем виде
(рис. 2.1а) для объемного напряженного состояния запишется:
|
|
|
|
1 |
|
|
|
|
τxу |
|
|
2(1 + ν) |
|
|
εx |
= |
|
|
|
[σx - ν(σy + σz )] |
γxу = |
|
= |
|
|
τxу |
|
||
|
|
|
|
|||||||||||
|
|
Е |
G |
E |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
τуz |
|
|
2(1 + ν) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
εy |
= |
|
|
|
[σy - ν(σx |
+ σz )] , |
γуz = |
|
|
= |
|
|
τуz . |
(2.10) |
|
|
|
|
G |
|
E |
||||||||
|
|
|
|
Е |
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
τzx |
|
|
2(1 + ν) |
|
|
εz |
= |
|
|
|
[σz - ν(σx |
+ σy )] |
γzx = |
|
= |
|
|
τzx |
|
|
|
|
|
G |
|
E |
|
||||||||
|
|
Е |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
В соотношениях (2.10) использована зависимость между тремя упругими постоянными материала – модулем упругости 1-го рода Е, коэффициентом Пуассона n и модулем упругости
2-го рода (модулем сдвига) G:
|
Е |
|
G = |
2(1 + ν) . |
(2.11) |
Формулы (23) показывают, что при изменении нормальных и касательных напряжений на всевозможных площадках, проходящих через заданную точку, соответственно изменяются относительные линейные деформации и углы сдвига граней выделенного элемента с беско-
нечно малыми размерами dx, dy, dz.
Совокупность линейных относительных деформаций и углов сдвига для всевозможных направлений осей, проведенных через заданную точку, называется деформированным со-
стоянием в точке.
Деформации элемента в трех ортогональных плоскостях представим в виде таблицы
|
|
|
|
1 |
|
|
1 |
|
|
|
|
εx |
|
|
γyx |
|
|
γzx |
|
||
2 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
γxy |
εy |
|
|
γzy |
(2.12) |
||
2 |
2 |
|
||||||||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
γxz |
2 |
|
γyz |
εz |
|
||
|
|
|
|
|
|
|
|
|
||
аналогичной тензору напряжений и называемой тензором деформаций.
Выражения (2.9) и (2.10), устанавливающие связь между деформациями и напряжениями в общем случае напряженного состояния, носят название обобщенного закона Гука. Они применимы при напряжениях, не превышающих предел пропорциональности материала и при малых деформациях.
С помощью формул (2.10) обобщенного закона Гука можно определять относительные деформации по любому заданному направлению, если предварительно определить нормаль-
ные напряжения вдоль указанного направления и двух других направлений, перпендикуляр-
ных заданному.
Относительные деформации ε1, ε2, ε3 в направлениях, для которых отсутствуют углы сдвига, определяемые по формулам (2.9), называются главными деформациями.
Для главных направлений тензор деформаций получит вид:
ε1 |
0 |
0 |
|
|
|
|
ε2 |
|
|
|
0 |
0 |
. |
|
|
0 |
0 |
ε3 |
|
|
|
|||
3.Гипотезы прочности
Вгипотезах прочности предлагаются критерии, определяющие прочность элемента материа-
ла, находящемся в сложном напряженном состоянии. Соответственно этим критериям уста-
новлены эквивалентные напряжения напряжения одноосного растяжения элемента материала, который равнопрочен тому же элементу при сложном напряженном состоянии. Вне зависимости от принятой гипотезы условие прочности элемента материала при любом напря-
женном состоянии имеет вид:
σэкв ≤ [ σp ]. |
(3.1) |
Для объемного напряженного состояния элемента эквивалентные напряжения имеют сле-
дующие значения :
по гипотезе наибольших нормальных напряжений

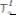
 = σ1 при σ1 > 0,
= σ1 при σ1 > 0,
по гипотезе наибольших линейных деформаций
σIIэкв = σ1 – µ(σ2 + σ3),
по гипотезе наибольших касательных напряжений
σIIIэкв = σ1 – σ3,
для плоского напряженного состояния:
σIII = σ 2 + τ 2
экв  4
4
по энергетической гипотезе
(3.2)
(3.3)
(3.4)
(3.5)
|
|
|
|
|
|
|
|
|
σIVэкв = |
1 |
[(σ |
1 − σ |
2 )2 + (σ |
2 − σ 3 )2 + (σ 3 − σ1 )2 ] , (3.6) |
|||
2 |
||||||||
|
|
|
|
|
|
|
||
для плоского напряженного состояния:
σIVэкв = |
|
. |
|
σ 2 + 3τ 2 |
(3.7) |
Достоинством этой теории является то, что она учитывает все три главные напряжения.
Она, как и 3-я теория, объясняет высокую прочность материала при всестороннем равно-
мерном сжатии, но не объясняет причины разрушения материала при всестороннем равно-
мерном растяжении.

ПРИМЕР 3.1
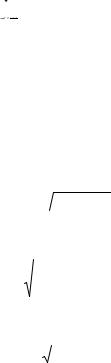
Даны напряжения на двух взаимно перпендикулярных площадках в окрестности некоторой точки (рис. 3.1). Е = 2,06 ×105 МПа, n = 0,28.
Требуется исследовать напряженно-деформированное состояние в данной точке.
1.Поставить знаки заданных напряжений в соответствии с их направлениями на рис. 3.1 согласно принятых правил знаков для напряжений.
2.Определить величины и направления главных напряжений, изобразить главные площадки на рисунке и показать на них главные напряжения
3.Вычислить максимальные и минимальные касательные напряжения, изобразить на рисунке площадки, на которых они действуют и показать направления напряжений. Вычислить и показать на чертеже действующие на этих площадках нормальные напряжения.
4.Определить нормальные и касательные напряжения на площадках, повернутых относи-
тельно заданных на угол
90 МПа ( σу )
 (τху)
(τху)
50 МПа
( τух )
80 МПа
( σх )
Рис. 3.1
a= 30 O , показать эти площадки и напряжения на них. Определить полное напряжение на этой площадке и относительную
деформацию по направлению sα.
5.Определить расчетные напряжения с использованием (1 ÷ 4)-й теорий прочности и сравнить их между собой, проанализировать применимость теорий прочности для конкретного материала.
6.Определить относительные деформации по направлениям главных напряжений (главные деформации).
РЕШЕНИЕ
1. Постановка знаков заданных нормальных и касательных напряжений: sх = 80 МПа, ("плюс" – растяжение),
sу = –90 МПа ("минус" – сжатие),
tух = –50 МПа ("минус" – против хода часовой стрелки). 2. Вычисление главных напряжений.
σ |
|
|
|
|
|
|
|
σx + σy |
|
1 |
|
|
|
|
|
|
|
|||
max |
= σ |
|
= |
|
± |
× (σ |
x |
- σ |
y |
)2 + 4τ2 |
= |
|||||||||
|
|
|
|
|||||||||||||||||
|
|
|
1,2(3) |
|
2 |
2 |
|
|
|
|
yx |
|
||||||||
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
80 - |
90 |
|
1 |
|
|
|
= – 5 ± 98,62. |
||||||||||||
= |
± |
× |
|
(80 + 90)2 + 4 × (-50)2 |
||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Соблюдая условие σ1 ≥ σ2 ≥ σ3, выпишем числовые значения главных напряжений:
σmax = s1 = –5 + 98,62 = 93,62 МПа,
σmin = s3 = –5 – 98,62 = –103,62 МПа, s2 = 0 (по условию задачи).
Проверка: sх + sу = s1 + s3 = 80 – 90 = 93,62 – 103,62 = –10 МПа.
Определяем угол наклона главных площадок к заданным:
tg2a0 |
= - |
2tух |
= - |
2 × (-50) |
= 0,588 |
; |
||
sх |
- sу |
80 + 90 |
||||||
|
|
|
|
|
||||
2a0 = 30,5°; a0 = 15,25°.
Угол положительный, поэтому заданные площадки должны быть повернуты против хода часовой стрелки и на полученных главных площадках показываем главные напряжения.
При этом максимальным напряжением будет то напряжение, которое проходит в четвертях, где сходятся стрелки касательных напряжений и оно будет находиться ближе напряжению σх, которое алгебраически больше, чем σу (рис. 3.1).
3. Определение максимального и минимального касательных напряжений на площадках сдвига:
|
|
|
τmax |
= ± (σ1 - σ3 ) |
= ± 93, 62 +103, 62 = ± 98,62 МПа. |
||
|
|
|
min |
|
2 |
2 |
|
Нормальные напряжения на этих же площадках будут: |
|
||||||
|
σα=±45° |
= σ1 + σ3 |
= 93, 62 -103, 62 = -5 МПа. |
|
|||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
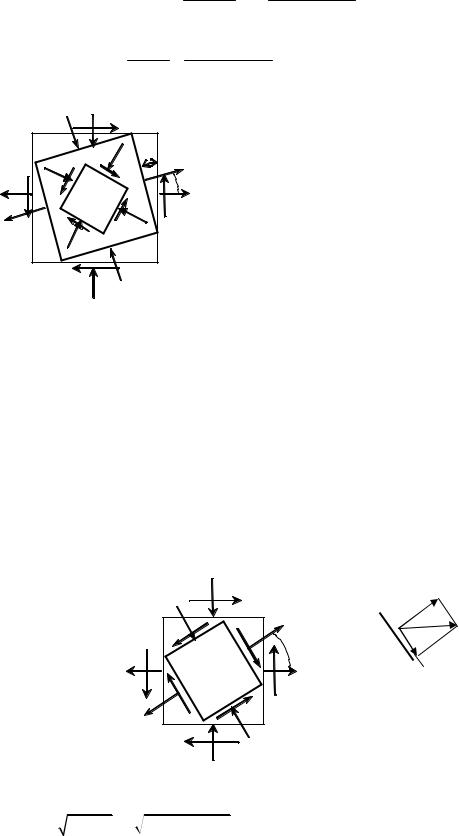
Покажем найденные напряжения на площадках сдви- |
|
|
σу |
|
|
|
|
га, наклоненных к главным на 45o (рис. 3.1). |
|
|
σ3 |
|
τху |
|
|
При этом направления максимального и минимально- |
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
σα=45 |
|
α0 |
|
σ1 |
го касательных напряжений покажем так, чтобы они |
|
|
|
|
|
сходились у того ребра элемента, где проходит глав- |
|||
|
τух |
τmax |
|
||||
σх |
|
|
α0 |
ное напряжение s1. |
|
||
τmin |
|
|
|
σх |
|
||
|
|
τmin |
|
4. Вычисление нормального и касательного напряже- |
|||
|
|
|
|
||||
σ1 |
τmax |
σα= –45 |
τух |
ний на площадках, наклоненных к заданным на углы |
|||
|
|
|
|
|
|
a = 30° и 30° + 90° |
|
|
|
|
|
|
|
sin 30o = 0,5, |
cos 30o = 0,866; |
|
τху |
σ3 |
|
|
cos 60o = 0,5, |
sin 60o = 0,866. |
|
|
σу |
|
|
|
Для этого используем формулы: |
||
|
|
|
|
|
|||
|
Рис. 4.8 |
|
|
σα = σx cos2α + σysin2α - τyx sin2α = 80 × 0, 7499 - 90 × 0, 25 + |
|||
|
|
|
+50 × 0,866 = 60 - 22,5 + 43,3 = 80,8 МПа; |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
σα+90° = σx sin2α + σycos2α + τyx sin2α = 80 × 0, 25 - 90 × 0, 7499 - |
|
|
|
|
|
|
|
-50 × 0,866 = 20 - 67, 49 - 43,3 = -90,8 МПа. |
|
Проверка:
sх + sу = sα + sα+90° ; |
|
|
|
|
|
|
|
|
|
80 - 90 = 80,8 - 90,8 = -10 МПа. |
|
|
|
|
|
|
|||
τα = |
σx |
− σy |
× sin2α + τyx cos2α = = |
80 + |
90 |
× 0,866 |
- 50 × 0,5 |
= 48, 61 |
МПа. |
|
2 |
2 |
|
||||||
|
|
|
|
|
|
|
|
||
На рис. 3.1 показаны наклонные площадки и напряжения, действующие на этих площадках c учетом их знаков. Угол a > 0, поэтому заданные площадки повернуты против хода часовой стрелки.
σα+90° |
σу |
τ |
σ |
α |
|
ху |
σα |
||
|
|
τα |
pα |
|
|
|
|
||
τух |
|
|
α =30° |
τα |
σх |
|
|
σх |
|
|
|
|
||
|
|
|
τух |
|
τху |
σу |
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.2 |
|
Определим полное напряжение на наклонной площадке: pα = 
 sα2 + tα2 =
sα2 + tα2 = 
 80,82 + 48,612 = 94,3 МПа.
80,82 + 48,612 = 94,3 МПа.
Относительную деформацию по направлению напряжения sα определим по формуле
εα = |
1 |
[σα - ν(σα+90° + σz )]= |
|
||||
Е |
|
||||||
|
|
|
|
|
|
||
= |
1 |
[80,8 |
- 0, 28(-90,8 |
+ 0)] = 51,57 ×10−5. |
|||
2,06 |
×105 |
||||||
|
|
|
|
||||

5. Определение расчетных напряжений по четырем теориям прочности и их сравнение:
1-я теория прочности – теория наибольших нормальных напряжений:
sIР = s1 = 93, 62 МПа,
sIР = s3 =103, 62 МПа.
2-я теория прочности – теория наибольших относительных удлинений: sIIР = s1 - n(s2 + s3 ) = 93, 62 - 0, 28(0 -103, 62) =
=122, 63 МПа.
3-я теория прочности – теория наибольших касательных напряжений: sIIIР = s1 - s3 = 93, 62 +103, 62 =197, 24 МПа.
4-я, энергетическая теория прочности:
σIVр = 
 1 [(σ1 - σ2 )2 + (σ2 - σ3 )2 + (σ1 - σ3 )2 ] =
1 [(σ1 - σ2 )2 + (σ2 - σ3 )2 + (σ1 - σ3 )2 ] =
2
=1 [(93, 62 - 0)2 + (0 +103, 62)2 + (93, 62 + 103, 62)2 ] = 2
=170,89 МПа.
Сравнительный анализ расчетных напряжений siР показывает, что наибольшее по абсолютной величине расчетное напряжение получается по третьей теории прочности. Значит, если в данном случае использован пластичный материал, то за расчетное напряжение нужно брать это напряжение и условие прочности записать в виде:
sIIIР =197, 24 МПа £ R.
Если же предполагается, что материал хрупкий, то нужно использовать вторую теорию прочности и условие прочности должно быть записано в виде:
σIIР =122, 63 МПа £ R t .
6.Вычислим относительные деформации по направлениям главных напряжений (главные деформации), используя формулы обобщенного закона Гука (2.9):
ε |
|
= |
1 |
[σ - ν(σ |
|
+ σ |
|
|
)] = |
1 |
[93, 62 - 0, 28(0 -103, 62)] = |
||||||||
|
|
|
|
|
|
|
2, 06 ×105 |
||||||||||||
|
1 |
|
|
Е |
1 |
|
2 |
|
3 |
|
|
|
|
||||||
= 59,53 ×10−5 ; |
|
|
|
|
|
|
|
|
|
|
|||||||||
ε |
|
= |
|
1 |
|
[σ |
|
- ν(σ + σ |
|
)] = |
|
1 |
|
|
[0 - 0, 28(93, 62 -103, 62)] = |
||||
|
|
|
|
|
2, 06 ×105 |
|
|
||||||||||||
|
2 |
|
|
|
Е |
|
|
2 |
|
1 |
|
|
3 |
|
|
|
|
||
=1,36 |
×10−5 ; |
|
|
|
|
|
|
|
|
|
|
||||||||
ε |
|
= |
1 |
|
[σ |
|
- ν(σ + σ |
|
|
)] = |
1 |
|
[-103, 62 - 0, 28(93, 62 + 0)] = |
||||||
|
|
|
|
|
|
2, 06 ×105 |
|
||||||||||||
|
3 |
|
|
|
Е |
|
|
3 |
|
1 |
|
2 |
|
|
|
|
|||
= -63, 03 ×10−5. |
|
|
|
|
|
|
|
|
|
|
|||||||||
4.Сложное сопротивление стержня
4.1Внутренние силы при сложном сопротивлении стержня
Правила построения эпюр при пространственном загружении стержня несколько от-
личаются от правил, принятых для построения эпюр усилий в стержне, на который действует нагрузка, расположенная в одной плоскости.
Перечислим эти отличия.
1.Эпюры Qx и Qy строятся на одной оси.
Эпюра строится в аксонометрии, причем ординаты Qx откладываются по оси х, ординаты
Qy ‒ по оси у.
Положительные значения поперечных сил откладываются в отрицательном направлении соответствующих осей.
Такая результирующая эпюра поперечных сил обозначается просто Q.
2.Эпюры Mx и My строятся на одной оси.
Эпюра строится в аксонометрии, причем ординаты Mx откладываются перпендикулярно оси х (по оси у), а ординаты My по оси х.
Положительные значения изгибающих моментов откладываются в положительном на-
правлении соответствующих осей (как в балках).
Полученная результирующая эпюра изгибающих моментов обозначается Mи. Знаки на эпюре Mи не ставятся.
При построении эпюр изгибающего момента Mx в балках положительные значения Mx
откладываются вниз (в положительном направлении оси у и перпендикулярно оси х). В соот-
ветствии с правилом знаков при положительном изгибающем моменте в сечениях балки рас-
тягиваются нижние волокна (волокном здесь называются совокупность точек, лежащих на линии, параллельной продольной оси z).
Таким образом, можно сказать, что положительные значения момента Mx на эпюре откладываются «от растянутого волокна». Более того, чтобы не связывать эпюру Mи с выбо-
ром системы координат, знаки на эпюре не проставляются.
Если при построении пространственной эпюры поперечных сил Q возникают затруд-
нения с определением знака, полезно использовать правило: при нисходящей эпюре изги-
бающего момента поперечная сила положительна.
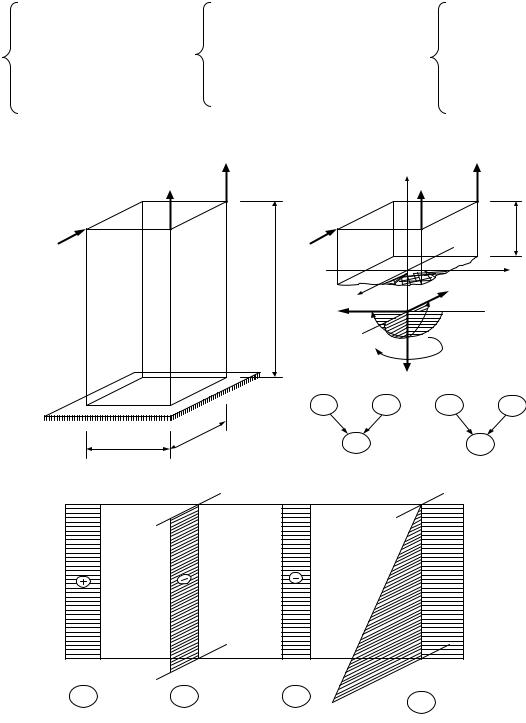
Задача 4.1 Построить эпюры внутренних сил для стержня, изображенного на рис. 4.1.
Решение
Воспользуемся методом сечений в чистом виде. Реакции в заделке в данном случае можно не определять, если рассматривать равновесие верхней части стержня.
Итак, проводим сечение на расстоянии z от верхнего края стержня. Нижнюю часть стержня отбрасываем. Действие нижней части стержня на верхнюю заменяем 6-ю неизвестными компонентами внутренних сил. Поскольку их значения неизвестны, изначально будем считать их положительными. (Штриховкой показаны плоскости действия моментов Мх и Му).
Для отсечной части стержня запишем шесть уравнений равновесия:
∑Х=0 ∑Y=0 ∑Z=0
∑mx=0 ∑my=0 ∑mz=0
− F − Qx = 0 |
Qx=F |
− Qy = 0 |
Qy=0 |
F + F – N = 0 |
N=2F |
F· 3a +F·3a − Mx =0 |
Mx= − 6 Fa |
− F·z + My = 0 |
My=Fz |
− F·3a − Mк = 0 |
Mк= − 3 Fa. |
Эпюры N и Mк (так обозначается момент относительно оси z – крутящий момент)
cтроятся на отдельных осях. Направление откладываемых ординат произвольно.
Рис. 4.1
Эпюры Qy и Qx строятся на одной оси (каждая в своей плоскости). Положительные значения откладываются в отрицательном направлении оси. Эпюры называем Q.
Эпюры Мх и Му строятся на одной оси. Значения Мх откладываем по оси у и наоборот
− Му - по оси х. Положительные значения откладываем в положительном направлении осей.
Во избежание путаницы с наименованием осей, общую эпюру изгибающих моментов назы-
ваем Ми.
Задача 4.2. Построить эпюры внутренних сил для стержня, изображенного на рис. 4.2.
Решение
Построить эпюры усилий в данном случае можно не определяя реакции в заделке, ко-
торые в данном пространственном случае представлены шестью неизвестными компонентами.
Границы участков на рис. 2 пронумерованы, и в каждом из этих сечений показана со-
ответствующая система координат.
Так же, как и в балках, строить эпюры в данном случае можно «эскизным» способом,
например, «по границам участков».
Для упрощения процесса построения эпюр рекомендуется:
1. Все внешние силы, действующие на стержень, привести к продольной оси z с по-
мощью теоремы о параллельном переносе силы, которая иллюстрируется рис. 4.3. Так, при перенесении силы F1 по оси х добавляется момент M1 = F2·а, при перенесении силы F2 по оси y добавляется M2 = F2·2а, при перенесении силы F3 в точку С1 добавляется в вертикаль-
ной плоскости момент М3 = F3·2а и в горизонтальной плоскости М4 = F3 · а .
2. Используя принцип независимости действия сил разбить всю нагрузку на три группы:
А) Нагрузку, проектирующуюся на оси z или вызывающую относительно ее момент.
Это M1 , M2 и F3 .
Б) Нагрузку, вызывающую прямой поперечный изгиб в вертикальной плоскости. Это
F1 , М3 .
В) Нагрузку, вызывающую прямой поперечный изгиб в горизонтальной плоскости.
Это М4 и F2 .
Нагрузка группы А вызывает в сечениях стержня продольное усилие
N = - 4P и крутящий момент Мк = 2Ра на правом участке стержня. Каждая из этих эпюр строится на своей оси. Чтобы не привязывать эпюру к определенной координатной системе,
соответствующая на рис. 4.2 обозначена Мк .
Эпюры от нагрузки группы Б и В строятся как для обычной консольной балки : от из-
гиба в вертикальной плоскости yz - эпюры Qy и Mx (ось x - вниз). Схема на рис. 4 помогает уяснить, как направление внешнего момента связано со знаком изгибающего момента. Про-
ще говоря, где стрелка - там сжатая половина сечения.
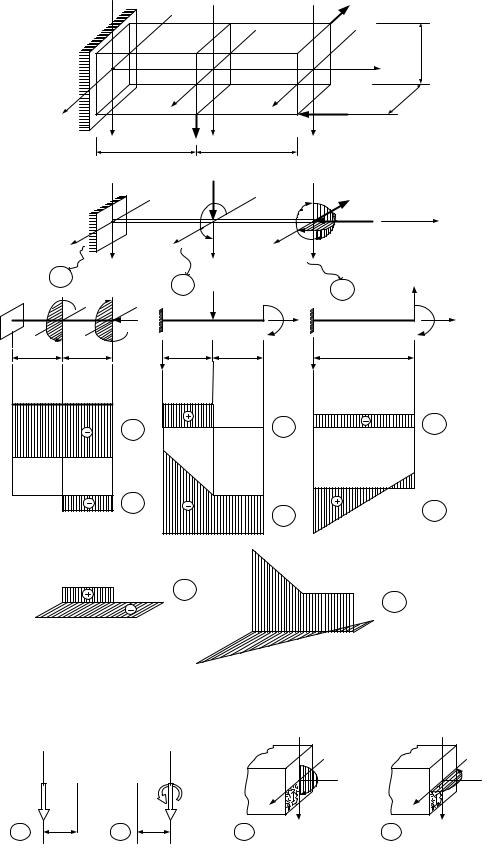
Рис. 4.2
Рис. 4.3 |
Рис.4.4 |
