Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

8071

.pdf

Скачиваний:

Добавлен:

23.11.2023

Размер:

1.35 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Таблица 2 -Варианты заданий к лабораторной работе № 2

№	k							ai			bi		№						ai					bi
1	5,10,15		3 + 1									i	16						1					4
														4
				√ + 1
				√ + 1
2	4,8,12		5 + 3										17	1										2 +


					3 −											(2 − 1)
					3 −											(2 − 1)
3	3,7,11	+ 3									1		18	1										5 +

		2 + 1														(2 − 1)
		2 + 1														(2 − 1)
4	5,9,13				2 −						1		19				1							4 − 1
																	16 − 1

					√ + 1
					√ + 1
					√													1						5
5	7,10,13				√	+ 1					i+4		20					1						5
																		4 − 1
		2 + 5
		2 + 5
6	5,10,15				− 1						3i–1		21		(−1)								1

				√ + 4
				√ + 4
7	8,12,16										2 – 1		22	(−1)								1		3 − 2
																					3 − 2
				√ + 2
				√ + 2
8	5,10,15										2 + 1		23	(−1)								1		3 − 1
																					3 − 1
			3 √
			3 √						+ 1
9	7,11,15	3									4i - 3		24	(−1)								1		2 − 1
																					2 − 1

					√ + 2
					√ + 2
10	5,9,13										4 − 2		25		(−1)							1

		3 √
		3 √					+ 1
11	4,9,14	1									2		26	(−1)								1		(2
																				(2 − 1)				− 1)
		2
		2
12	3,8,13	1									3i+5		27	(−1)								1		(2
																				(2 − 1)				− 1)
		3
		3
13	4,8,12		(−1)							1	4( + 1)		28	(−1)										(
										1														(
																								+ 1)
										5
										5				( + 1)
14	5,8,11		(−1)							1	7 + 2		29											5
										1														5
															(4 − 1)
										5
										5
15	4,6,8	1/( + 1)									3 + 2		30											9 − 2

															(9 − 1)
															(9 − 1)

Контрольные вопросы

1.Какой алгоритм называется разветвляющимся?

2.Назовите оператор безусловного перехода.

3.Назовите оператор условного перехода.

4.Какие формы записи имеет оператор IF?

5.Запишите линейную конструкцию оператора IF.

6.Коков смысл используемых в программе переменных?

7.Что такое переменная в языке программирования?

8.Запишите операторы подсчета суммы и произведения членов ряда.

Лабораторная работа №3

Тема:Табулирование функции. Применение табулирования к решению уравнения f(x)=0.

Цель работы:Составление программы табулирования функции y= f(x)и ее использование для нахождения корня уравненияf(x)=0 с заданной точностью.

Варианты заданий лабораторной работы №3 приведены в таблице 3.

Работа состоит из двух задач:

Задача 1. Найти таблицу значений функций y= f(x)на отрезке [a, b] с шагом h.

Задача2.Вычислить корень уравнения f(x) = 0на отрезке [a, b] с точностью

ε=0,005.

Перед выполнением задания любого уровня необходимо проверить графически, что на заданном отрезке [a, b] находится корень уравнения. Если корня на заданном отрезке нет, то следует определить по графику новый отрезок,

содержащий корень, и при решении задачи рассматривать его. График привести в отчёте.

Задание (1 уровень)

1. Графически получить приближённое решение уравнения f(x) = 0.

Уравнение взять из таблицы 3. в соответствии с номером своего варианта.

2. Составить блок-схему алгоритма табулирования функции f(x) на отрезке

[a, b] с шагом h=0,1.

3.Составить программу табулирования функции f(x) на отрезке [a, b] с

шагом h=0,1.

4.Ввести программу, выполнить её, получить и выписать 11 пар значений

(x, y).

5. Для вычисления корня уравнения f(x) = 0найти и выписать

отрезок[ , ], полученный в результатах табулирования, на концах которого

f(x)имеет разные знаки.

6.Повторно запуская программу табулирования, получить таблицу значений функции f(x)на отрезке[ , ]с шагомh=0,1.

7.С экрана выписать новый отрезок [ , ], на концах которого функция

f(x) имеет разные знаки. Вычислить середину этого отрезка &1 = ( + )/2– это

ибудет приближённый корень уравнения f(x)=0, с точностью ( = 0,005.

8.Вычислить значение функции в корне. Выписать полученные результаты.

Задание (2 уровень)

1. Графически получить приближенное решение уравнения f(x) = 0.

Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.

2. Изменить блок-схему задачи табулирования функции f(x), предусмотрев возможность повторного запуска алгоритма табулирования на новом интервале с новым шагом h ( = | − |/10). Выход из программы должен быть выполнен,

если длина найденного интервала окажется меньшелибо равна заданной погрешностиε (| − | ≤ (). Перед выходом вычислить корень уравнения как середину последнего отрезка и значение функции в корне.

3.Составить программу табулирования f(x) на [a, b] с шагом hпо новой блок-схеме.

4.Запустить программу, получить результаты по табулированию функции

f(x)последовательно на данном интервале [a, b] с шагом h=0,1 и на каждом новом

интервале [ , ] , где функция меняет знак на противоположный, с шагом

= | − |/10.

5.С экрана выписать результаты табулирования на первом интервале, а для последующих результатов – выписывать две строки, где функция меняет свой знак. Выписать корень уравнения и значение функции в корне.

Задание (3 уровень)

1. Графически получить приближённое решение уравнения f(x) = 0.

Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.

2. Составить блок-схему и программу, реализующие алгоритм вычисления корня уравнения f(x)=0 на интервале [a, b]с заданной точностью ( . Для нахождения корня использовать алгоритм табулирования функции f(x),

последовательно уменьшая в 10 раз интервал поиска[ , ], где .( ) .( ) < 0

пока не выполнится условие: | − | ≤ (.

Замечания:

а) на каждом отрезке[ , ]проводить не более 10 вычислений значений

функции f(x);

б) приближенным решением уравнения считать середину последнего

отрезка &1 = ( + )/2.

3. Ввести программу, выполнить её и получить результат. На экран вывести границы каждого нового интервала поиска корня, корень уравнения, заданную

точность и значение функции в корне.

Таблица 3- Варианты заданий к лабораторной работе № 3

№	Уравнение	Отрезок [а,	№	Уравнение	Отрезок
вар.	Уравнение	b]	вар.	Уравнение	[а,b]
вар.		b]	вар.		[а,b]

01 + & − 2 = 0

[0;1]

22& − 21 = 0

[0;1]

[1;2]

01 − 10& = 0

[3;4]

2 − 2 ln & = 0

21 − √

= 0

[0.1;1.1]

01 = 2– &

[-1;0]

45 & + √

= 0

[0.1;1.1]

2– & = lg&

[1;2]

– ln & = 0

[2;3]

√

+ 1 =

[0.1;1.1]

2& + 75(2& + 3)

31– √2& = 0

[0;1]

= 1

– 21

√& + 2

[-2;-1]

&21– 1 = 0

[0;1]

= 0

2 ln & – 2& = 0

[0.1;1.1]

& – &– 2 = 0

[1;2]

21– & = 0

[0;1]

& – 2&– 4 = 0

[1;2]

& – 2√

= 0

[-0.5;0.5]

х + 11 = 0

[-1;0]

= 0

[0.1; 1.1]

& + ln & = 0

[2;3]

& – √2&

[0.2;1.2]

& + 75(7 + &)

[0;1]

√&– & + 1 = 0

= 3

+ 2√

= 0

[0.1; 1,1]

& + 4 sin & = 0

[-0.5; 0.5]

(&– 1) = 0,5 01

[0;1]

ln & – sin & = 0

[2; 3]

(&– 1) = 01

[1;2]

sin & + 2& = 1

[0;1]

Контрольные вопросы

1.Какой алгоритм называется циклическим?

2.Какие существуют виды циклических алгоритмов?

3.Какую структуру имеет оператор организации циклов с известным числом повторений?

4.Зарисуйте базовую алгоритмическую структуру, соответствующую оператору For.

5.Что называется табулированием функции?

6.Как применить табулирование к решению уравнения?

7.Почему из результатов табулирования выбирается отрезок с разными знаками функции на концах?

8.Как рассчитывается приближённый корень уравнения на найденном отрезке?

Лабораторная работа №4-5

Тема:Одномерные массивы.

Цель работы:Приобретение навыков разработки алгоритмов и программ по преобразованию одномерных массивов.

Варианты заданий лабораторной работы приведены в таблицах 4.1, 4.2.

Задание (1 уровень)

1. Составить блок-схему алгоритма вычисления функции Y=f(X). Функцию f(X) взять из таблицы 4.1 в соответствии со своим вариантом.

2.Разработать программу вычисления элементов массива Yна основе элементов массива X, где Y=f(X). Массив X взять из таблицы 4.1 в соответствии со своим вариантом.

3.Выполнить программу, записав полученные результаты в отчёт.

Задание (2 уровень)

1. Составить блок-схему алгоритма вычисления наибольшего и наименьшего элементов в массиве Y, их порядковых номеров, а также суммы всех элементов массива Y. Массив Y получить на основе элементов массива X, где:

Y=f(X). Функцию f(X) взять из таблицы 4.1 в соответствии со своим вариантом. 2. На основе блок-схемы, составленной в п.1 разработать программу.

Массив X взять из таблицы 4.1 в соответствии со своим вариантом.

3. Выполнить программу, записав полученные результаты в отчёт.

Задание (3 уровень)

1.Составить блок-схему алгоритма для задания, описанного в таблице 4.2 в

соответствии со своим вариантом.

2.На основе блок-схемы, составленной в п.1 разработать программу.

3.Выполнить программу, записав полученные результаты в отчёт.

Таблица 4.1 - Варианты заданий к лабораторной работе № 4

x2 × ex , x < 0

x < 0

1 + x 2

0 £ x < 1

y =

0 £ x £ 5

y = x

1 + x

× e

−x

, x ³ 1

x > 5

+ x

x = {2.1; 0.3; 0.7; −1.2; − 3.1; 0.6; − 3.5; 2.7}

x = {1.8; 1.2; - 1.6; - 0.2; 6.3; 0.3;

0; - 1.9; 9}

[1]

[2]

x × e

, x £ 0

x + 2

, x £ 0

x - 2

y = e , 0 < x < 2

y =

- 2,

0 < x < 2

× e

−x

x ³ 2

(4 - x)

x = {1.5;2.0;-1.1;0.4;0.6;- 0.7;1.7;3.2;0.1}

x = {- 0.3; - 3.6; 4.7; 1.0; 3.9; 1.5; - 0.8; 1.2; 2

[3]

[4]

− x

, x <10

x + 2

- x - 2

1 - e

y = 1 + e

10 £ x <15

10− x

15 £ x

y =

+ 2,

x £ -1

x - 2

x ³1

3 - x,

x ={0.1;-5.7;- 2.7; 17.5;- 4.7;-7.3; 16;7.8;10.9}

x = {-1.1;1.3; - 4.3; - 2.5; 2.3; 1.7; 2.8; 4.3; -

[5]

[6]

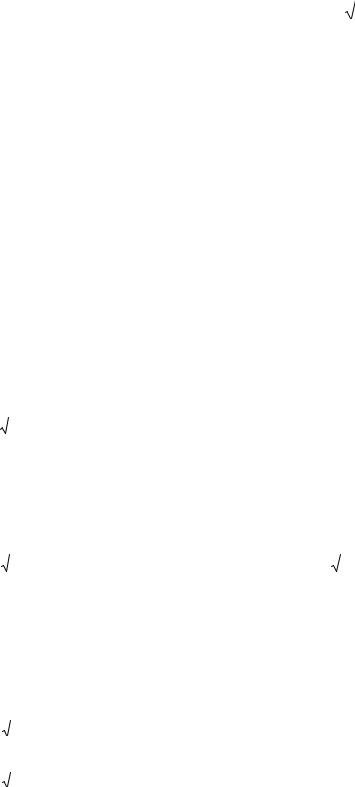
e − x ,

x < 0

ln(- x),

x < -1

0 £ x £ 1

y =

y = -

1- x

-1 £ x £1

e x ,

x > 1

ln(x),

x >1

x = {2.0; 0.9; - 0.3; 0.7;1.4; - 0.6;0.5;2.3}

x = {- 0.4; 0.7; -1.6; 2.6; - 2.2; 1.2; 2.1}

[7]

[8]

2 × 2x+1 ,

x < 1

x < -3

7.6292 + x,

1 £ x £ 2

- x,

- 3 £ x < 3

y = 2x + 2x+1

y = e

(e x / 3 + e−3 / 2 ), x ³ 3

× x

- x

+1, x > 2

x ={-0.2; 3;1.5; 2.7; -0.6; 0.4; 0.9; 4.5; 1.3}

x = {- 3.3;-1.0;-1.5;2.1;4.4;-1.4; 5.0;- 4.0}

[9]

[10]

- e × ln(- x)

x £ -1

x 2

− x − 1,

x ≤ −1

− 1 < x ≤ 0

y = − x 2 − x + 1,

y = ln(- x),

- 1 < x < 1

x ³ 1

− x

+ x + 1,

x > 0

1 - x

x = {- 3.1;3.9;2.5;-1.3;1.7;3.5;- 0.6;0.8}

x = {0.8;-1.6;1.6;- 0.3; - 2.0;-1.3;1.9}

[11]

[12]

2 + x,

x < -1

- x -1,

x < -1

1- x

+1, -1 £ x £ 1

- x

-1

£ x £1

y =

y = 1

- x,

x > 1

> 1

x -1,

x = {0.3;1.7; 0.1; 0.6; 2.8; - 0.8; - 0.5; -1.4}

x = {-1.1; 0.7; -1.4; 0.2; -1.6; 3.9; - 0.8; - 0.2}

[13]

[14]

x < -1

2 × 2x+1 ,

x > 2

-1 - x

- x

-1 £ x £ 1

+ x4 ,

0 £ x £ 2

y = 2

y = 2x

x > 1

2 × x4 - x2 +1, x < 0

x -1,

x = {0.3;1.7;0.1;6; -1.8; - 0.8;- 0.5;-1.4;0.5}

x = {2.2; - 2.7; -1.9;1.1; -1.4; 1.4; - 2.5;0.8;-

[15]

[16]

x 2 - x -1 2 , x £ -1 2
	2 - x + 2, -1 2 < x £ 1
y = - x
	2	+ x +1 2 , x > 1
- x

x = {1.8; 0.9; 1.1; - 1.4; - 0.3; - 0.5; - 0.1}

[17]

	- 2 - x				,		x < -2
	×	x	- x	2		,	- 2 £ x £ 2
				2
y = 2

	x - 2,						x > 2
	x - 2,						x > 2

x = {- 2.8; 2.5; - 0.4;1.8; -1.4; 0.8;1.2;-1.9;3.

[18]

sin x x ,

x < -π

+ 1,

x < −1

1 − (x + 2)2

- π £ x £ π

y = sin x × sin 2x,

1 − x

+ 1,

− 1 ≤ x ≤ 1

y =

x > π

1 − (x − 2)2

+ 1,

x > 1

sin x x ,

x = {- 0.6; 0.9; - 1.7; 4.1; - 4.4; - 0.3;1.4}

x = {2.3; - 1.0;

- 1.3; - 1.7; 0;1.2; - 0.4; 2.8

[19]

[20]

x > 2

e1+ x - x,

x £ -1

(x − 2)5

+ 2,

− 2

≤ x ≤ 2

-1 £ x £ 1

y = x

y =

− (x

− 2)2 ,

x < −2

1− x

+ x,

x > 1

x = {- 3.2; - 0.3;1.5; 7; - 0.6; - 2.4; 0.9; 5;1.3}

x = {-1.5; 2.8; - 2.7; 2.7; 0.7; - 0.3; 2.4; 0.2}

[21]

[22]

x < −1

ln(- x)

x £ -2

y = x + x, − 1 ≤ x ≤ 1

- 2 < x < 2

y = ln(- x)+ 3,

x > 1

x - 2,

x ³ 2

x = {1.8; 0.9;1.1; -1.4; - 0.3; 0.5; 2.1}

x = {1.8; - 0.9; - 2.3; 3.8; - 2.7; 1.2;1.1; - 1.3;

[23]

[24]

x2 × ex , x < 0

cos x

x ,

x < -π

2 ,

0 £ x < 1

-π £ x £ π

y = x

y = cos x ×sin 3x,

× e

−x

, x ³ 1

x > π

cos x,

x = {- 2.8; - 0.4;1.8; - 1.4; 0.8;1.2;-1.9;-1.0}

x = {- 4.6; 0.2; 3.9; - 1.7; 1.1; - 0.4; - 3.3; 0.

[25]

[26]

−

− 1,

x < −π

- 1,

x < - 4

y = sin x,

− π ≤ x ≤ π

£ x £

y = tg x,

− 1,

π < x

< x

x = {0.2;- 0.2;3.5;0.3;5.7;1.0;-1.9;- 5.3}

x = {0.2;-1.2; 0.5;0.3; - 0.3;- 0.5;1.4}

[27]

[28]

-1 < x <1

+ 5,

x < -1

+ 2 x

- 2

- x

+ x, -1 £ x £ 1

y = x

y =

+ 2,

x £ -1

x - 2

x > 1

x + 2,

x ³1

- 5

x = {3.3;3; 0.9;- 2.9; - 2.2;-1.3;1.7;2.4}

x = {- 3.1;3.9; 2.5;-1.3;1.7; 3.5; - 0.6;0.8}

[29]

[30]

Таблица 4.2 - Варианты заданий к лабораторной работе (3 уровень))

№

Задание

вар.

1Дан массив А из N натуральных чисел. Постройте алгоритм для определения среднего арифметического и среднего геометрического данных чисел. Среднее геометрическое:

Aср = N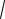 A1 A2 ... AN .

2Имеется массив А из N вещественных чисел. Составьте алгоритм решения задачи: заменить все элементы массива, не принадлежащие отрезку [0, 1], на 0.5. Вывести на печать исходный массив и результирующий.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.20231.35 Mб08067.pdf
#
23.11.20231.35 Mб08068.pdf
#
23.11.20231.35 Mб08069.pdf
#
21.11.2023153.1 Кб0807.pdf
#
23.11.20231.35 Mб08070.pdf
#
23.11.20231.35 Mб08071.pdf
#
23.11.20231.35 Mб18072.pdf
#
23.11.20231.36 Mб08073.pdf
#
23.11.20231.36 Mб08074.pdf
#
23.11.20231.36 Mб08075.pdf
#
23.11.20231.36 Mб08076.pdf