
7926
.pdf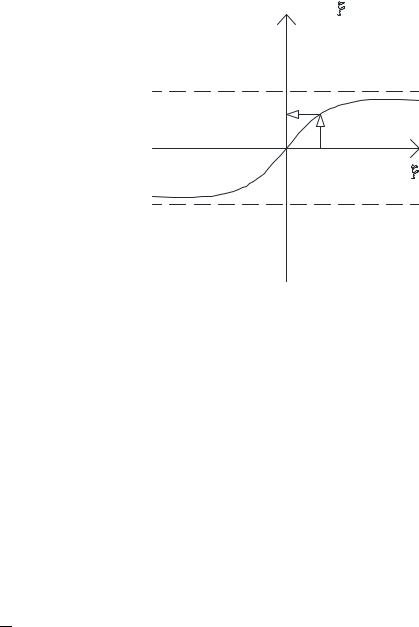
|
|
|
|
|
|
81 |
|
Подставив значения констант в уравнение (4) получим выражение для поля |
|||||||
температуры: |
|
|
|
ÏŠ7 $E |
|
||
T – T c = (T0 – T c) √h ξ(>ξ |
|
||||||
Выражение |
|
|
Š7 |
и |
= Ф(ξ) = e·r·f(ξ) получило название интеграл |
||
|
функция |
производная по ξ табулированы |
(составлены |
||||
вероятности и эта |
√h |
(> Ï |
|
|
$E |
|
|
таблицы): |
|
|
|
|
|
|
|
Поэтому мы можем окончательно наше решение записать в виде: |
|||||||
|
|
|
|
T – T c = (T0 – T c) · e·r·f( √DÌ4) |
(3.74) |
||
|
|
|
|
|
|
erf |
|
|
|
дополняет до |
|
||||
|
|
единицы |
+1 |
|
|||
|
|
|
|
|
|
erf |
|
|
|
|
|
|
|
-1 |
|
|
Рис. 3.23. График функции интеграл вероятности. |
|
|||||
По аналогии: cos2x = 1 – sin 2x
в математике и в физике введена функция, которую называют интервал
( Ï $E
дополнительный к интегралу вероятности. e·r·f·с(ξ) = 1 – e·r·f(ξ) = √h >ξ Š7
Эта функция также табулирована в справочниках. |
|||||||||||||||||
Для определения плотности теплового потока используем закон Фурье: |
|||||||||||||||||
|
|
|
*5 |
|
*5 * |
ξ = – λ |
-p |
! |
– p |
.· |
|
ŠD |
· |
|
|
||
q = – |
λ |
*D |
= – λ |
* |
ξ |
|
|
É |
|
· e |
|
√Ì4 |
(7) |
||||
В |
|
|
|
|
*D |
|
|
√h |
|
|
-Ì4 |
|
|||||
|
любой точке нашего полуограниченного массива q по (7) на поверхности |
||||||||||||||||
массива: |
= qc = x-p! – pÉ. |
|
|
|
|
|
|
|
|
|
|
||||||
2|D > |
(8) |
|
|
|
|
|
|
|
|
|
|||||||
|
|
√hÌ4 |
|
|
|
|
|
|
|
|
|
|
|
||||
a = Ryxz – можно подставить. |
|
|
|
|
|
|
|
||||||||||
82
3.15 Теплопроводность полуограниченного массива при граничных условиях 2 рода.
Формулировка задания такая же, как и в предыдущей задаче, но отличные
граничные условия. |
|
|
|
|
|
|||||||
при τ = 0; T = T0; |
*5 |
|
> |
|
||||||||
|
|
x = 0; q = – λ |
х |
= qc |
||||||||
|
|
x = ∞; T = T0-; |
*D. |
|
||||||||
рисунок, геометрические и физические условия соответствуют предыдущей |
||||||||||||
задаче. |
|
|
|
Ò |
5 |
|
|
|
|
|
|
|
Ò5 = a |
(1) |
|
|
|
|
|
||||||
Ò4 |
|
|
ÒD |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Продифференцируем левую и правую часть формулы (1) по переменной х и |
||||||||||||
домножим левую и правую части на (– λ) |
||||||||||||
Ò |
|
– |
|
Ò5 |
|
|
Ò |
|
|
|
*5 |
|
Ò4 |
( |
λ |
Ò |
) = a |
ÒD |
|
λ |
*D. |
||||
|
|
|
|
· (– |
|
|
||||||
Òm = a |
Ò m |
(2) |
|
|
|
|
|
|||||
Ò4 |
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
ÒD |
|
|
|
|
|
|
|
|||
Но тогда наша задача в точности похожа на предыдущую, если поменять в ней буквы.
τ = 0; q = 0 x = ∞; q = 0
Полностью можем использовать предыдущее решение, заменив TCH2 на q. |
||||||||||||||||||||||||||||
q – qc = (0 – qc) · e·r·f( √DÌ4) |
|
|
|
|
|
√Ì4 |
|
|
|
√Ì4 |
(4) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
определим, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
q = qc |
(1 – |
e·r·f( |
D ) = qc e·r·f·с( |
D ) |
||||||||||||||
Поле температур |
|
D |
|
|
|
|
используя закон Фурье: |
|
||||||||||||||||||||
q = – λ |
*5 |
= qc |
e·r·f·с( |
|
) = – |
|
λ |
*5 * |
ξ = qc |
e·r·f ( |
D |
) |
|
|||||||||||||||
*D |
|
|
|
|
* |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
√Ì4 |
|
|
|
|
|
ξ |
*D |
|
|
√Ì4 |
|
|
||||||||
– λ∂T = qc e·r·f ( √DÌ4) · ∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2√Y\ |
|
|
|
∞ |
|
|
|
|||||||||||||||||||
– ∂T = mλÊ e·r·f ( |
√Ì4 |
|
√Ì4 |
|
|
|
|
|
|
|
||||||||||||||||||
|
D |
|
|
) · ∂( |
D ) |
· |
|
55Ê $Ð = mÊ λ√Ì4 |
ξ ÏX³с-ξ. dξ |
|
||||||||||||||||||
– ∂T = mλÊ e·r·f·с(ξ) dξ · |
2 |
|
Y\ |
– |
|
|
||||||||||||||||||||||
(5Ê |
$Ð |
|
|
|
|
( |
|
ÏX³ -y. dy |
( |
|
|
|
|
|
|
( |
|
|
|
|
||||||||
5 |
|
= |
mÊλ√Ì4 |
|
ξ∞ |
|
|
с |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
T – T 0 = |
mÊλ√Ì4 i·e·r·f·c( |
D ) |
|
(5) |
|
|
|
|
|
|
|
|
|
|||||||||||||||
i·e·r·f·c(ξ) = ξ∞ |
|
|
|
с |
√Ì4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Интеграл от( |
|
ÏX³ -y. dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
дополнительного интеграла вероятности: |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
i·e·r·f·c(0) = |
|
; Tc – T 0 = |
mÊ√Ì4 |
|
|
(3.75) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√h |
|
|
|
|
|
√h·x |
|
|
|
|||
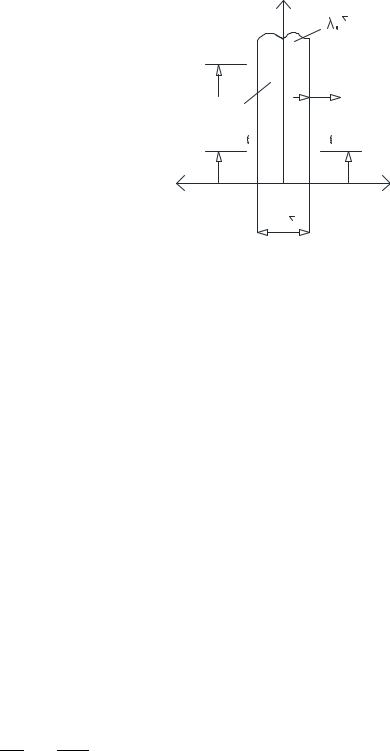
3.16 Нестационарное охлаждение плоской пластины.
83
Имеется плоская пластинка неограниченная по 0у.
T |
|
|
|
|
о |
T0 |
q |
|
F |
|
|
о |
|
о |
TЖ |
|
TЖ |
-x |
0 |
+x |
|
||
|
2о |
|
Рис. 3.24. Граничные условия для плоской пластинки.
Ò° |
= a Ò g |
(1) |
= T0 |
– T ж. |
||
τ = 0; T = T0; |
θ0 |
|||||
Ò4 |
ÒD |
|
|
|
|
|
|
|
-Ò4 |
. > 0 |
|
||
Пластина будет охлаждаться симметрично, тогда |
||||||
при х = 0; |
Ò° х |
.х « |
|
(2) |
||
|
х = δ; – |
λ-Ò°Ò4 |
α · θх=δ (3) |
|||
исходя из баланса энергии на поверхности.
Q’ – количество тепла, которое отдает пластина на любой момент времени τ
вокружающую среду.
Ксожалению, эту задачу нельзя решить с помощью подстановки Больцмана, используемой в предыдущих задачах, так как в этом случае решение удовлетворяет дифференциальному уравнению, но не удовлетворяет граничным условиям.
Фурье предложил решить эту задачу следующим образом:
неизвестную функцию θ(х, τ) представить в виде 2 неизвестных функций
θ(х, τ) = φ(τ) · ψ(х) (4)
Подставим (4) в уравнение (1), заменяя дифференцирование по времени точкойÔ, а дифференцирование по координате – штрихом.
φ ψ = a φ · ψ′′
Разделим левую и правую части на произведение φ · ψ |
|||||||||||||
φÔ·ψ = a |
|
φ· |
ψ |
|
|
|
|
||||||
φ ψ |
|
|
φ |
ψ′′ |
|
|
|
|
|||||
φ· |
|
|
ψ′′ |
· |
|
φ |
|
ψ′′ |
2 |
||||
|
Ô |
|
|
|
|
|
|
|
|
|
|
|
|
ψ |
|
|
|
; a · φÔ= ψ = – E |
|||||||||
φÔ |
= a ψ |
|
|||||||||||
φ + a E2 φ = 0 |
(5) |
|
|||||||||||
|
′′ + E2 ψ = 0 |
(6) |
|
||||||||||
φ = c1 · |
|
ÏŠ ·4Ì |
|
(7) – |
экспонента |
||||||||
84
ψ = c2sin(Ex) + c3cos(Ex) (8) – уравнение гармонических колебаний. Подстановка Фурье (4) позволила получить вместо одного
дифференциального уравнения частных производных 2 уравнения в полных производных.
Подставим (7) и (8) в соотношение (4) |
|
·4Ì |
|
|||
2 |
|
|
Š |
|
(9) |
|
θ(х, τ) =[ c2sin(Ex) + c3cos(Ex)] · c1 · |
|
|
|
|||
c1, c2, c3 и E – неизвестные |
постоянные. |
|
||||
|
Ï |
|
|
|
|
|
(9) – решение дифференциального уравнения (1)
Продифференцируем уравнение (9) по координате: |
|||||||||||||||||||
Ò° = E c1 |
|
|
|
|
|
|
|
|
·4Ì |
[c2 cos(Ex) – |
c3 sin(Ex)] (10) |
|
|
||||||
ÒD |
|
|
ÏŠ |
|
|
|
|
|
|
||||||||||
-ÒD. |
D > = E c1 |
Ï |
Š ·4Ì[c2 cos(0) – c3 sin(0)] |
|
|
||||||||||||||
Ò° |
|
|
|
||||||||||||||||
Тогда (9) будет иметь вид: |
|
|
|
||||||||||||||||
φ = c1 · |
Ï |
Š ·4Ì |
|
|
Ï |
Š ·4Ì |
|
|
|
||||||||||
θ(х, τ) = A |
· cos(Ex) |
|
|
(11) |
|
|
|||||||||||||
Подставим в (11) с учетом (10) в формулу (3): |
|||||||||||||||||||
– λ[(– A · E |
|
|
|
|
Š ·4Ì sin(Eδ)] = α · A · cos(Eδ) · |
Ï |
Š ·4Ì |
||||||||||||
δλEsin(Eδ) Ï |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Õ |
= α · cos(Eδ)δ |
|
|
|
||||||||||||
|
|
|
|
|
|
δ |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctg(Eδ) = |
|
αδ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ctg µ = ŵ |
(12) |
|
|
|
|
|
|
|
|||||||||||
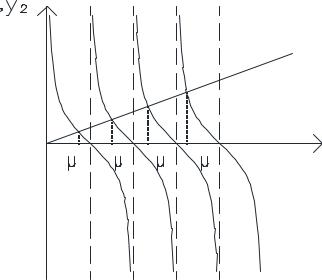
Соотношение (12) – это транцендентное уравнение для определения µ и Bi
y1 |
|
|
y2 |
|
|
|
|
1 |
2 |
3 |
4 |
Рис. 3.25. Функция ctg µ.
Каждому µn соответствует решение, которое удовлетворяет стационарному дифференциальному уравнению (1)

|
|
|
|
|
|
|
Ï |
|
85 |
θ1(х, τ) = A1 |
cos(µ1 |
· |
D) · |
Š ªÖ |
|||||
… 2 |
2 |
|
2 |
|
« |
|
Š |
Ö |
|
|
· |
«D |
) · |
Ï |
ª |
||||
θ |
(х, τ) = A cos(µ |
|
|
|
|
|
|||
θn(х, τ) = An cos(µn · D) · |
|
Š ªÖ |
|||||||
Любое решение, |
которое удовлетворяет дифференциальному уравнению (1), |
||||||||
|
|
« |
|
Ï |
|
|
|||
граничным условиям (2), (3), но не одному из них не удовлетворяет наименьшее условие.
Но известно, что ∑ частных решений является также решением этого дифференциального уравнения и удовлетворяет граничным условиям (2) и (3).
Подчиним эту ∑ решений начальным условиям задачи. |
|
|
|
||||||||||||||||||||||||||||||||||||||
θ(х, 0) = |
|
∞ |
|
|
|
|
|
D |
|
|
= θ0 |
|
(13) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D) · ax |
|
|
|
|
|||||||
Помножим левую и правую части на cos(µ |
m |
и проинтегрируем по |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
× cos -• |
|
«. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
толщине пластины. |
|
|
|
|
|
|
Û « cos- • · C. · $C |
|
« |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
« |
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
D |
|
|||||||||||||||||
θ0 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
Š« |
∞ |
|
|
|
|
|
« |
à |
|
D |
|
|
|
|
|
||||||||||
|
|
|
Š« |
|
cos- • |
|
· |
« |
. · $C |
|
|
∑ |
× |
|
Š« |
cos- • · |
« |
. · cos- • |
· |
« |
. · $C |
||||||||||||||||||||
|
|
( |
|
|
|
|
D |
|
|
|
|
D |
|
|
|
( |
|
|
|
|
|
||||||||||||||||||||
|
« |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
0; Ý & |
_ |
|
|
|
|
|||||||||||||
Š« |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Функции, обладающие« |
такими« |
свойствами, называют ортогональными. |
|||||||||||||||||||||||||||||||||||||||
( |
|
|
|
cos- • |
|
|
· |
|
|
. · cos- • |
|
· |
|
|
. · $C |
|
|
ÜÝ 0; & |
|
|
|
|
|
||||||||||||||||||
В правой части все члены ряда кроме одного, для которого m ≠ n будут |
|||||||||||||||||||||||||||||||||||||||||
равны нулю. |
|
(µª£ª |
ºÞ¸- ·ª.·*D |
|
|
|
|
|
|
|
¸ß¢ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
An = θ0 |
|
= θ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
(µª£ª ºÞ¸ - ·ª.·*D |
|
|
|
|
¸ß¢ · ºÞ¸ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставим A в решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
cos |
|
|
¬ |
½1nM cos 2¬¾ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
θ = θ0 |
· |
|
|
|
|
∞ |
|
|
|
|
¸ß¢ |
|
|
|
|
|
|
|
|
|
|
|
D |
|
(14) |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
∑ |
|
¸ß¢ · ºÞ¸ · cos- • · «. · ˜ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Анализ полученного решения.
Приведем решение к безразмерному виду.
θ= T(х, τ) – T ж
θ= f (x, τ, δ, λ, a, α, θ0)
ОбозначимDбезразмерныеÌ4 величины большими буквами:
Θ = θθ!; X = «; F0 = «
F0 – |
безразмерное время сил |
|
|
|
число Фурье |
|
|
||
|
Å |
0 |
|
|
ctg µ = |
¸ß¢ · ºÞ¸ · cos- • · à. · exp -€• |
· '>. |
|
|
|
∑ |
|
||
Разделим (14) на θ : |
|
|
||
Θ = |
∞ |
¸ß¢ |
|
(14’) |
Θ = F(x, F0, Bi) (15)
86
Соотношение (15) мы могли бы получить вообще не решая нашу задачу, а просто приводя к безразмерному виду дифференциальное уравнение и краевые условия к нему.
Так как µn представляет собой ряд возрастающих чисел:
µ1 < µ2 < µ3 Видно, что каждый последующий член ряда будет меньше (по модулю)
предыдущего.
Из-за cos(µn · X) этот ряд будет знакопеременным.
S = U1 – U2 + U3 – U4 +…
Из теории знакопеременных рядов известно, что при нахождении частичной суммы сумма отброшенных членов ряда будет меньше последнего удерживаемого слагаемого.
Доказано, что при значении F0 ≥ 0,3 ряд (14’)настолько быстро сходится,
|
|
|
|
|
¸ß¢ · ºÞ¸ · cos- • · à. · ÏŠ ·)! |
|
|||||
что достаточно ограничиться в расчетах первым членом ряда. |
|
||||||||||
|
|
¸ß¢ |
Θ = |
¸ß¢ |
|
|
|
|
|
(3.76) |
|
|
|
= N(Bi) |
|
|
|
|
|
|
|||
|
¸ß¢ · ºÞ¸ |
|
|
|
|
|
|
|
|
||
Для центра пластины: |
|
|
Š ·)! |
· '> |
|
||||||
|
|
|
|
|
Θx=0 = N(Bi) · |
|
(3.77) |
||||
|
|
|
|
|
ln Θx=0 = ln N( |
B ) – |
• |
(3.78) |
|||
|
|
|
|
|
|
Ïi |
|
|
|
|
|
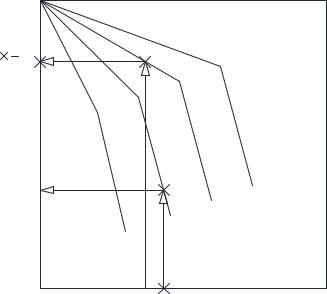
Линейная зависимость от безразмерного времени. Номограмма.
1
O 

Bi1
Bi2
0 |
F0 |
Рис. 3.26. Линейная зависимость Θ от безразмерного времени Fо.
о Ì4« F =¥·«
Bi = x
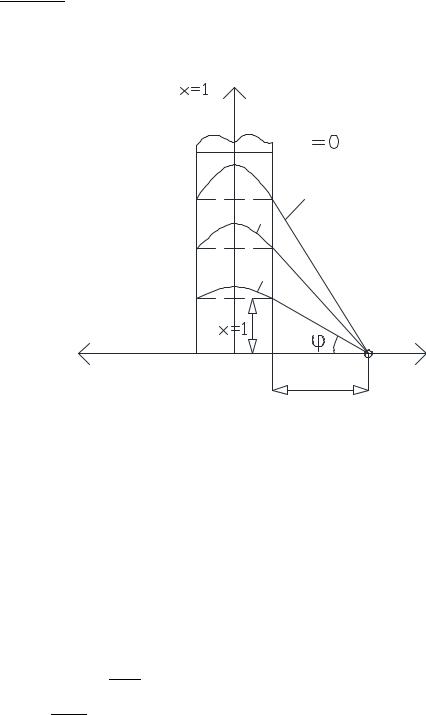
87
5->,4.Š5 θ = 5!Š5ж ж
Такая же номограмма построена для поверхности пластины.
Θx=1
|
О |
|
|
|
|
|
F0 |
|
|
|
F02 |
F0 |
|
|
|
|
|
|
|
|
F03 |
|
|
|
|
О |
|
|
|
-x |
0 |
x0 |
A |
+x |
|
|
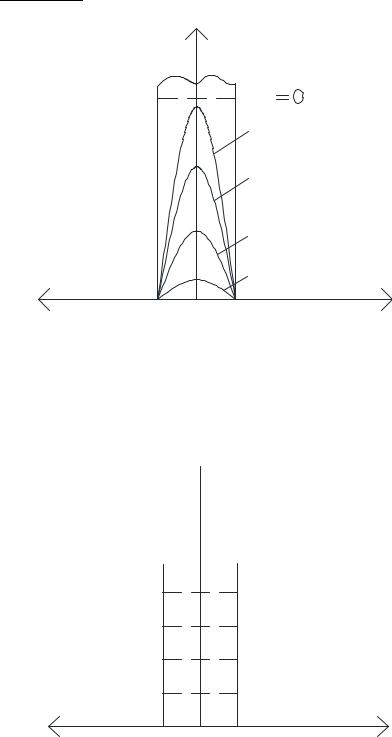
Рис. 3.27. Зависимость Θ от безразмерного времени Fо для поверхности пластины
Касательные, проведенные к температурным профилям в точках их пересечения с поверхностью стенки пересекаются в точке А, которая
располагается на оси абсцисс и находится на расстоянии от стенки = х0. |
||||||||||||||
x0 = |
|
|
|
|
|
D |
|
|
|
|||||
|
Òä.D « |
|
|
|
|
|
|
|||||||
– ( ÒΘÅ |
|
|
|
= ¥ Θx=δ |
(краевые условия) |
|||||||||
|
Ò- |
|
. |
|
¥ · « |
|
θ |
|
|
|
||||
– |
θ |
= |
|
δ |
||||||||||
|
|
θ |
|
|||||||||||
|
! |
|
|
|
|
|
|
|||||||
|
|
θ |
|
|
x - !.D |
|
|
|||||||
|
Ò-θ . |
|
|
|
|
|||||||||
– |
-ÒD.D |
= Bi · Θx=1 |
||||||||||||
Ò ª |
|
|
|
|||||||||||
– |
Ò |
|
|
|
|
= tg φ = |
|
|
¤ |
|||||
|
-ÒD.D |
|
Θ |
|
|
|
|
|
ä! |
|||||
|
θ |
|
|
|
|
|
|
|
|
Θ |
|
|||
Bi · Θx=1 = |
|
¤ |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
ä! |
|
|
|
|
|
|
|
|
|
Bi → ∞ (Bi > 100) |
|
|
|
||
ctg µ = 0; µ1 |
= h; µ2= h; …; |
µn= - Š .h |
|
|
|
|||
|
|
|
|
|
|
|
- |
ž · '>¾ |
Θ = |
∑ |
- Š .h · cos n |
ž · ào · exp ½€ |
|
||||
|
∞ |
-Š . £ |
Š |
|
- Š . |
|
||
|
|
Θ = h- cos h à · exp -€ h- · '>. |
|
|
||||
|
|
|
|
|
||||
(3.79)
(3.80)
Эту зависимость часто используют для расчёта температуры в центре
пластины. |
· exp -€ h- · '>. |
Θx=0 = h- |
|
|
|
|
|
|
|
|
|
88 |
|
exp -h- · '>. = hΘ-¤! |
|
|
||||||||
Прологарифмируем и разделим на h . Получим |
|
|||||||||
F0 = - ln |
h |
Θ- |
= |
Ì4 |
→ |
- |
|
|||
h |
· |
|
¤! |
ж |
« |
(16) |
|
|
||
τ = « - |
|
--5!Š5 |
. |
|
|
|||||
|
Ì |
|
|
|
|
|
ж |
|
|
|
h |
|
h½5->,4.Š5 ¾ |
О |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F0 |
|
|
|
|
|
|
|
|
|
|
F01 |
|
|
|
|
|
|
|
|
|
|
F02 |
|
|
|
|
|
|
|
|
|
|
F03 |
|
|
|
|
|
|
|
|
|
|
F04 |
|
|
|
|
|
-x |
|
|
0 |
A |
+x |
|
|
|
|
|
|
|
|
|
|||
Рис. 3.28. Зависимость Θ от безразмерного времени Fо внутри пластины |
||||||||||
2)Bi → 0 (Bi < 0,1) ctg µ = Å = ∞
О 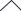
F0

F01
F02
F03
-x |
0 |
A |
+x |
|
|
Рис.329. Пошаговая зависимость Θ от безразмерного времени Fо внутри пластины
89
µ1 = 0; µ2 = π; …; µn = (n – 1) π |
|
||||||||||||||
|
åæç |
|
|
|
|
|
|
|
|
|
|||||
µ |
· |
µ |
|
|
|
|
|
|
= 1 |
|
|
|
|||
lim 9> åæç ºÞ¸ |
|
|
|
|
|
|
|||||||||
|
|
|
|
µ |
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Все члены ряда, кроме 1, равны нулю. |
|
||||||||||||||
ctg µ= |
ºÞ¸ = |
|
= |
|
|
→ |
|
= Bi |
|
||||||
Первый член ряда равен 1. |
|
|
|||||||||||||
|
¸ß¢ |
|
Å |
|
|
|
|
• |
θ = 1 · exp(– Bi · F0) |
(3.81) |
|||||
cos(µ1 X) © 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определение количества теплоты, отданной пластиной.
|
T |
|
|
T0 при |
|
|
T1 при |
|
|
F |
|
|
Tж при |
|
-x |
0 |
+x |
|
||
|
2о |
|
|
Рис. 3.30 Граничные условия. |
|
|
|
от τ = 0 до τ = ∞; Q’п = ρ2δFcp(T0 – T ж) (1) |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
от τ = τ до τ = ∞; Q’ |
|
= ρ2δFc ( |
|
– T |
|
|
) (2) |
|
|
|
|
|
|
|
||||||||||||||
|
|
от τ = 01до τ = τ1; |
1 |
|
|
|
p 11 |
|
|
ж |
|
|
! |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ж |
|
|
|
||||
|
|
|
|
Q’ = Q’п – Q’ 1 = ρ2δFcp(T0 – T |
ж) · |
[1 – 5 |
– 5ж] = Qп · [1 – |
θ |
] |
(3.82) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
момент времени τ |
|
(Фурье 1) сводится к |
||||||||||
|
|
Таким образом расход теплоты на |
|
|
|
|
|
5 – 5 |
|
1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
∑ |
|
|
¸ß¢ · ºÞ¸ |
|
· cos- • |
· à. · e |
|
|
|
|
|
|
|
|
|||||||||||
расчету на этот момент времени средней температуры пластины. |
|
|||||||||||||||||||||||||||||
|
|
Θ = |
|
|
|
¸ß¢ |
|
|
|
|
|
|
|
|
|
|
|
|
Š ·)! |
(4) |
|
|
|
|
|
|||||
|
|
|
(> |
∞ |
|
· dx ¸ß¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
D |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= { |
|
|||||||
|
|
θ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Θ |
= |
|
D |
Θ |
– среднеинтегральное значение. |
|
( |
cos-• · à. · $C |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
· e |
Š ·)! |
· |
|
( |
|
|
cos-• |
· à. · $C |
|||||||||
|
|
|
|
¸ß¢ · ºÞ¸ |
|
|
|
|
> |
|
|
|
|
|
> |
|
||||||||||||||
= |
∑ ∞ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
¸ß¢ ä} = |
∑ |
|
¸ß¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.83) |
||||||||
|
|
|
|
|
¸ß¢ · ºÞ¸ |
· eŠ ·)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
90
3.17 Уравнения конвективного теплообмена в безразмерном виде
2 = 2к + 2т = ρ cpT – λ · grad T (1)
Чтобы найти поле температур текущей жидкости, надо найти поле скоростей в этой жидкости. Для их определения необходимо привлечь 5 дифференциальных уравнений: уравнение энергии, 3 уравнения движения в проекциях на оси x,y,z и уравнение неразрывности или сплошности, причем каждому из 5 уравнений необходимо задать краевые условия.
К сожалению, дифференциальные уравнения движения нелинейны.
В то же время по закону теплоотдачи Ньютона мы могли бы раслит-т плотность теплового потока, определив коэффициент теплоотдачи.
Коэффициент теплоотдачи сам зависит от поля температуры текущей жидкости.
На самой стенке жидкость неподвижна и может быть рассчитана q = – λ (Ò5Ò7.7 > = α[Ty=0 – T ж]
λ – коэффициент теплопроводности жидкости.
x-èÎ.P¤! α p èP – p
= – é¤! ж (2)
y
x
Рис. 3.31. Поле скоросте в двумерной области.
Теория подобия процессов конвективного теплообмена позволяет ответить на вопросы:
