Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

7923

.pdf

Скачиваний:

Добавлен:

23.11.2023

Размер:

1.27 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

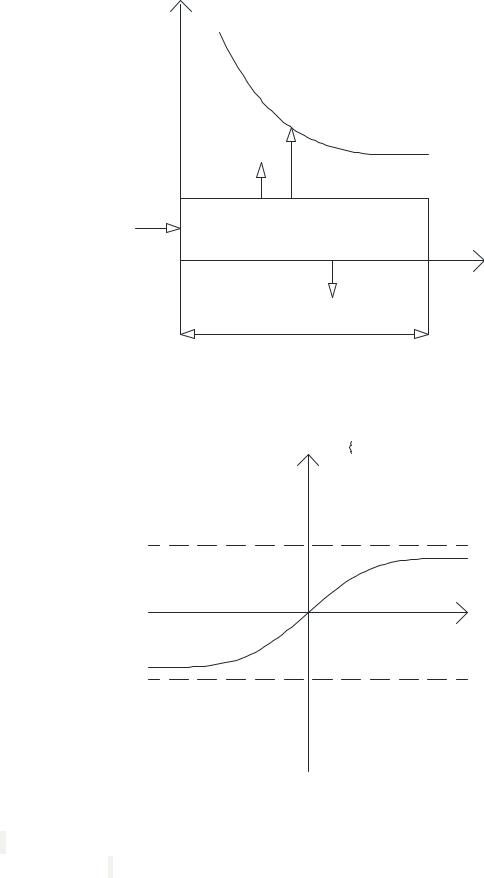
		71
		Qp
		Qp
		0
		l
		Рис.3.16. Теплообмен на ребре
		=ch α – гиперболический косинус
´¦ ´µ¦		=ch α – гиперболический косинус
´¦Š´µ¦		=sh α – гиперболический синус
		tho
		+1
		-1
(sh α)’		Рис. 3.17. Гиперболический тангенс.
(sh α)’	º¹= ch α
th α =	¸¹ αα – гиперболический тангенс
(ch α)’ = sh α
Если формулу (6) домножим и разделим на двойку, то получим гиперболический

косинус

»¼½ -•ŠD.¾

θ=θ y¼- •. (7)

Для нахождения потока тепла, который рассеивается ребром конечной длины

используем закон Фурье:

p = –

λ ·

(

*θ)

0 – закон Фурье

*D y¼- •.

¿À½

-˜ € C.¾

Продифференцируем значение (7):

*θ =

· [–

]

Подставим значение производной при х = 0 в выражение потока тепла:

p = λ ·

θ · »¼- •.

= {

¥z“

, подставим и внесем λ под корень} = θ1

±¬0²ˆ³

y¼- •.

L x¯

· th(

)

Qp= θ1

²ˆ³

· th(ml)

(3.68)

Если l → ∞, то th(ml) → 1.

3.11 Стационарная теплопередача через оребрённую стенку.

ТС2-TЖ2

o F11

TЖ1	о	TЖ2

Q1
F1
	b
о	l

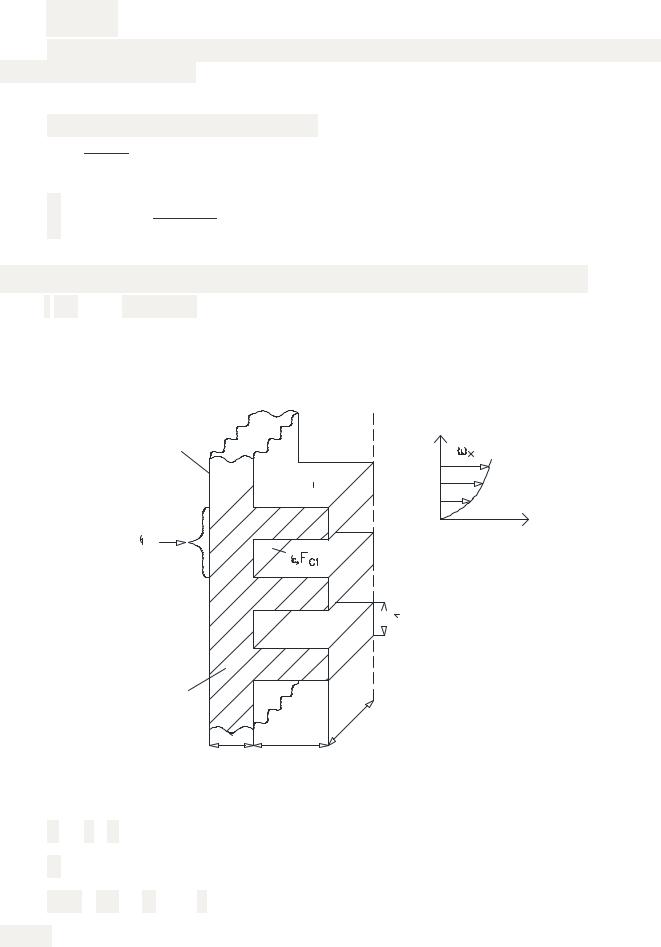
Рис. 3.18. Стационарная теплопередача через оребренную стенку

F1 = n · F11

Q1 = TС2 – T ж2 ©

U = 2 · b + 2 · δ 2b f = b · δ

Подставим в m = L¥x¯z“ и получим:

L¥z Á L ¥z« m = xÁ« = « x

Критерий (число) Био:

Bi = ¥xz« – число Био (3.69)

Безразмерные числа, состоящие из величин, заданных по условию задачи, называют критериями.

Безразмерные числа, состоящие из незаданных по условиям задачи величин, называют числами.

Физический смысл критерия Био:

«¨x Bi = ¨¥z

Критерий Био представляет собой отношение термического сопротивления теплопроводности стенки к термическому сопротивлению теплоотдачи.

Если окажется, что Bi >> 1, то можно пренебречь термическим сопротивлением теплоотдачи по сравнению с термическим сопротивлением теплопроводности.

Если Bi << 1, то в данной задаче можно пренебречь термическим сопротивлением теплопроводности по сравнению с термическим сопротивлением теплоотдачи.

Если Bi ≈ 1, то надо учитывать оба сопротивления.
Тогда формулу (8) мы можем переписать в виде:
Qp1 = θ1	±¬02ÂˆÂÃ				•
		¬0		·	• = {Fp1 = 2 · b · l, боковыми поверхностями ребра
					Ÿ ª±
пренебрегаем} =			· Fp1 · θ1		ª± Å
					Ä¼Ÿ	Å
Qp1 = ¬0· Fp1 · θ1 · E
ªŸ± Å		– коэффициент эффективности ребра.
E = Ä¼ªŸ± Å

Bi → ∞; E = 0

Bi → 0; E = 1 (по первому и второму замечательным пределам)

Qp1 = αÆ· Fp1 · θ1 · E Qc1 = αº· θ1 · Fc1

Q1 = Qp1 + Qc1 = (αÆ· Fp1 · E + αº · Fc1) · θ1 = αпр · Fрc1 · θ1

Fрc1 = Fp1		+ Fc1		)рÉ
αпр = αÆ		)рÇ	· E + αº
	È É			È É

Приведенный коэффициент теплоотдачи – это некий осредненный коэффициент теплоотдачи на оребренной поверхности стенки.

Если мы обозначим поток тепла через всю стенку, то

Q = n Q1

а приведенный коэффициент теплоотдачи в этом случае будет равен:

Fp = Fp1 · n; Fрc = Fрc1 · n

αпр = αÆ È)рÇÉ

M αº È)рÉÉ

Поскольку поток тепла в стационарной задаче через любую стенку

постоянен Q = const

′-Тж – Тс .

l α

· '

-5Ê Š5Ê .

· ' · -Tº – T .

αпр

рс—

Перепишем эту систему так, чтобы справа остались только температурные

разности:

· )′

· l Тж – Тс

x· )

l 1

€ 1

· )

· l Tº

– T

tαпр

рс

Сложим эти равенства:

Тж Šp′

Q =

(3.70)

· Ë

—· Ë

· Ë

αпр

рс

Если отнести поток тепла к неоребренной поверхности F1, то получим плотность теплового потока на левой поверхности стенки:

)		ª—			· ËË
q1 = 3	=		Тж′ Špж				–	плотность теплового потока на неоребренной
		α		αпр		рс

поверхности.

)

)рс – вся поверхность справа, отнесенная ко всей поверхности слева, называется

коэффициентом оребрения.

Если коэффициент оребрения больше 1, то плотность теплового потока q1 при этом возрастает.

3.12 Стационарная теплопередача и теплопроводность плоской стенки с внутренними источниками тепла.

Будем полагать в этой задаче, что свойства металла стенки постоянны (теплофизические) и плотность внутренних источников тепла qv = const

Для решения этой задачи используем общее дифференциальное уравнение

теплопроводности.		m		`p			x
`p
`	τ = a 2 T +	Ryz	;	`	τ	= 0, a =	Ryz
		\|
2 T + mx\| = 0 (1)

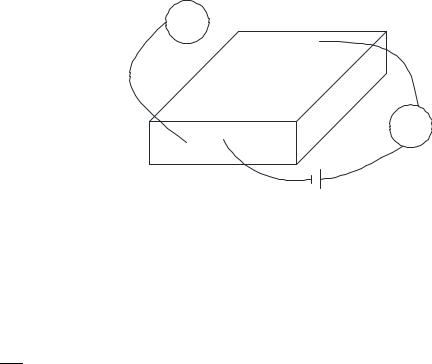
Допустим, плоская пластина толщиной 2δ и с боковой поверхностью F находится в движущейся среде, температура которой вдали от пластины Tж.

Пусть коэффициент теплоотдачи (α) постоянен.

	T
		q
TЖ	о		о	TЖ
	о		о
	F
-x		0		+x
-x				+x
		2о

Рис. 3.19. Граничные условия на плоскй пластине толщиной 2δ.

В стационарной задаче нет надобности задавать краевые условия.
	`p
При х = 0; q = 0;	`	τ = 0
x = δ; – λ · f(*5)x=0= α				ж		δ
T = T(x) = ?; q =*D				-T € T .\|	D
T = T(x) = ?; q =*D				-T € T .\|
	?; Q		= ?_

Будет выделяться Джоулева теплота:

Q = I · U

Рис. 3.20. Схема для выделения Джоулевй теплоты.

3g = qv

Если Тж = const и α = const, то температура в пластине будет изменяться

только по толщине пластины, по другим координатам она меняться не будет.

ðp

5 = 0

`b `c

ðb

+ m| = 0 (2)

даже

Так

как

пластина охлаждается симметрично, то не зная,

можно

утверждать,

что он

будет симметричен относительно плоскости

yz (центра

- .

плоскости).

= 0

ðх

Тогда мы можем рассмотреть при решении половину этой пластины,

толщиной δ, полагая при х = 0 – это половина пластины теплоизолирована.

q = - λ-*5*D.D > = 0

†p

x + C1

†a

€ x

dT =

xdx + C dx

T =

€m|xx2 + C1 x + C2 (6)

общее решение дифференциального уравнения (2) , где С , С

–

какие-либо

€

константы.

Подставим (3) в (5) при х = 0

С1 = 0

Подставим в формулу (6) соотношения (4) и (5) при х = 0

Тх=δ = Тс = € mx|δ2 + С2 – λ (- mx| δ) = α [€ mx| δ2 + C2 – T ж]

(3.71)

	mα\|δ + m\| + Tж = C2
		x
	Подставим эту константу в формулу (6) и получим окончательное
выражение для поля температуры:
	= m\|(δ2			- х2) +	mα\|δ	+ Tж (7)
		x		δ			δ
	T\|D >			x				+ Tж (8)

			= T0 = m\| + mα\|

При прочих равных условиях увеличение толщины пластины в 2 раза приводит к увеличению температуры в середине в 4 раза.

Например, тепловыделения для сферы при работе внутренних источников тепла пропорциональны r3, а теплопотери – поверхности r2.

†p†a = € mx| x

Для определения поля плотностей теплового потока и плотности теплового потока отдаваемого тепла в окружающую среду

Используя-*5.закон Фурье, мы имеем: q = - λ *D = qv · x (9)

qx = δ = qc · δ

Количество тепла, подаваемого за единицу времени с поверхности стенки в окружающую среду, будет равно в стационарном теплопроводном режиме количеству тепла, которое выделяется внутри этой стенки за счет работы внутренних источников.

1\|		δ · F
Qc = qx = δ · 2F = qc · δ · 2F= qv · V = qv 2
	D «= Tc = mα\|δ + Tж (11)
Полностью решили задачу.
Так как при α → ∞ задача теплопередачи выраждается в задачу
теплопроводности, действительно, при этом из (11)

Tc = Tж → следовательно нам заданы граничные условия 1 рода.
Для поля температуры в этом случае из соотношения (7) мы получим:
T = mx\|(δ2 - х2) + Tc	(3.72)

3.13 Стационарная теплопередача и теплопроводность круглого стержня с внутренними источниками тепла

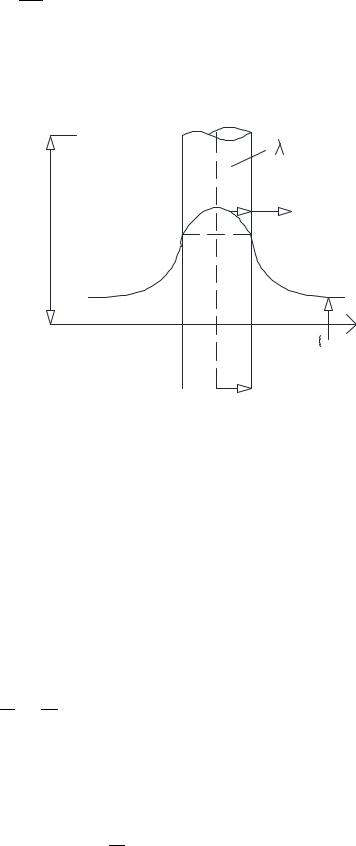
Изнутри подводится тепло.

qv = const †p

при r = 0; †’ -=*50.(1) T

r = r0; - λ *D • •!= α [ ’ •! – T ж] (2)

T = T(r) = ? qc = ? T0 = ? Tc = ? Qc = ?

В силу условий охлаждения стержня Tж = const не зависит от координат. Поле температуры в этом стержне будет одномерным, то есть температура меняется только по радиусу.

ðp				m		x
ð	= a 2 T +			\|	; a =
τ						Ryz
2 T + m\|			= 0Ryz
†’		x	x
		• *•				– в цилиндрической системе координат.
†	5	+ *5	+ m\| = 0 (3)

q
l		TЖ
		TЖ
0	о	r
r0

Рис. 3.21. Граничные условия для теплопередачи и теплопроводности круглого стержня с внутренними источниками тепла.

Сделаем подстановку в уравнение (3):

U =

*5;

*“

= † 5

*“

*•

†’

U + m| = 0

*•

•

Умножим левую и правую часть на r·d

rdU + Udr = –

m|r · dr –

дифференциальное произведение 2х функций.

d(U · r) = –

m|r ·xdr

Проинтегрируем левую и правую части:

U · r = – m|r2x + С1

Разделимxна r:

U =

*5 = –

r +

*•

•

Умножим на dr:

dT = –

m|r · dr + C1*•

m| x

•

T = –

-x

r2 + C lnr + C

(4)

решение для (3) уравнения

Подставим (5) в (1): 0 =

→ C1 = 0

Подставим в (2) (4) и (5)>

-x

- λ(–

· r0) =

[–

m|r2 + C2 – T ж]

m|·α•!

C =

-x

Найденные константы C1 и C2 мы подставим в (4):

T = –

(

–

) + m|·α•!

+ Tж

(6)

T =

-x

X>=

+ T

(7)

T|• >

m| 0

m|·α•!

T =

-x

+ T

• •!

m|·α•!

соотношение (5) найдем поле плотностей

Используя

закон Фурье

теплового потока в стержне:

q = - λ-*5*D. = m|· •

(8)

· 2π r0 l = m|•! h•!• = qv · π

l = qv V

(3.73)

Qc = qc · F = qc

выраждается в задачу теплопроводности,

При α → ∞ задача теплопередачи

то есть:

Tc = Tж

–

) + Tc ,

T = m| (

решать задачу при граничных условиях 1 рода.

если-x

3.14 Нестационарная теплопроводность полуограниченного массива

(без внутренних источников тепла, граничные условия 1 рода)

Полуограниченный массив

–

плоская стенка,

толщина которой

равна

бесконечности.

Рис. 3.22. Полуограниченный массив.

–∞ < y < +∞

–∞ < z < +∞ 0 < x < +∞

τ = 0; T = T0; x = 0; T = Tc ≠ T0

Будем полагать, что в начальный момент времени при τ0 = 0, то

при х = 0: T = Tc ≠ T0

при х = ∞; T = T0

`5T(x, τ)`=5?; qc = ? `• = a `’ (1)

Для решения этой задачи используем подстановку Больцмана:

ξ =

√Ì4

(1)

–

√Ì

(

– 4√4

) =

ξ ·

`5 `

√Ì4

(

`-ÍÎ.

`D `D.

√Ì4 `

√Ì4

Ì4

Подставим это все в дифференциальное уравнение (1):
		`5			- ` 5
– 4	· ξ	`		=	4 `
`ξ5	· ξ			=
`ξ5			`5		ξ
`			ξ		ξ
`			`
	+ 2ξ			ξ	= 0 (2)

Подстановка Больцмана позволит свести дифференциальное уравнение частной производной к дифференциальному уравнению полной производной.

Преобразуем начальные и граничные условия нашей задачи.

5!√ŠÑ5Ê

Tc > T0

при τ = 0; TD = T0; ξ = ∞ τ = 0; ξ = √Ì4

x = 0; T = Tc; ξ = 0 x =∞; T = T0; ξ = ∞

Обозначим†5 † 5 : †“

†ξ = U; †ξ = †ξ

Перепишем†“ уравнение:

†ξ = – 2 ξ U

Разделим†“ на U и помножим на:

“ = – 2 ξ dξ

Интегрируем

Ïξ

lnU = –

ξ2

+ lnC

U =

ξ · c

(55Ê $Ð =Ï

(>ξÏŠ7 $E

dT= c ·

Š dξ

ÏŠ7 $E

T – T c = c (>

∞

ÏŠ7

Пусть в этом решении ξ → ∞, тогда из (3) T0 – T c = c

= √h → c =

†

ÏŠ

· /

†5

(5)

ξ=

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.20231.27 Mб07919.pdf
#
21.11.2023152.63 Кб0792.pdf
#
23.11.20231.27 Mб07920.pdf
#
23.11.20231.27 Mб07921.pdf
#
23.11.20231.27 Mб07922.pdf
#
23.11.20231.27 Mб07923.pdf
#
23.11.20231.27 Mб07924.pdf
#
23.11.20231.28 Mб07925.pdf
#
23.11.20231.28 Mб07926.pdf
#
23.11.20231.28 Mб07927.pdf
#
23.11.20231.28 Mб17928.pdf