7805

понятие функциональной зависимости и ввести понятие функции

n

действительных переменных, т.е. функции нескольких переменных.

Пример

1.

Площадь

S

треугольника

является

функцией

двух

независимо друг от друга изменяющихся переменных – основания

a

треугольника и его высоты h : S

1 a h f (a, h).

2

Пример 2. Работа тока

A на участке электрической цепи зависит от

разности потенциалов U на концах участка, силы тока I

и времени

t . Эта

функциональная зависимость задается формулой:

A I U t f ( I, U, t ).

Пусть имеется n переменных величин, тогда множество всех

упорядоченных наборов их значений X (x1 , x2 ,..., xn ) из

n действительных

чисел называется n -мерным числовым пространством n .

Элементы

пространства

n

можно интерпретировать как точки с

координатами

x1 ,

x2 ,..., xn и обозначать M ( x1 , x2 ,..., xn ).

Если каждой точке X ( x1 , x2

,..., xn ) из некоторого множества D n

z , то говорят, что на множестве D

задана функция z f ( x1,

x2 ,..., xn )

n действительных переменных, т.е.

z f (X ) , со значениями в

. При

обозначает закон соответствия. Множество

D D ( f ) называется областью

определения функции. Множество значений, принимаемых функцией

z

в

n 2

. Поэтому в данном пособии будем подробно рассматривать случай двух

Геометрически каждая совокупность значений двух переменных

x

и

y

изображается точкой

на

плоскости. Область

определения

функции

z f ( x, y) представляет

собой некоторую

совокупность точек

плоскости

O x y .

Совокупность значений трех переменных x , y

и z изображается точкой

в пространстве. Область

определения

функции трех переменных

-3

0

3

x

-1 0

1

x

Решение. Функция определена при условии, что

1 y 1

и при любых

значениях x . Следовательно,

область определения

функции

есть полоса,

заключенная между двумя прямыми y 1 и

y 1,

включая и эти прямые

(рис. 3).



y

1

y=1

-3

0

3 x

Линией уровня функции двух переменных

z f ( x, y) называется

линия f ( x, y) C на плоскости O x y ,

в точках которой функция сохраняет

постоянное значение z C

. При этом число C называется уровнем.

Геометрически придание функции

z постоянного значения C означает

пересечение поверхности

z f ( x, y)

плоскостью

z C , параллельной

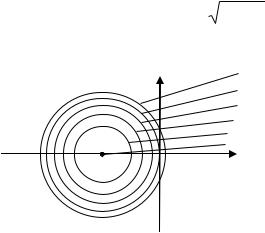
Пример 6. Построить линии уровня функции z x

2

y

2

4 x .

y

C=1

C=0

C=-1

C=-2

C=-3

C=-4

-2

0

x

Число A называется пределом функции

z f ( x, y)

в точке

M 0 ( x0

; y0 )

(или, что то же самое, при

x x0 и

y y0 ),

если абсолютное значение

разности

f ( x, y) A

будет меньше любого заранее заданного сколь угодно

малого положительного числа , когда для всех точек M ( x; y)

расстояние

M M 0

меньше некоторого положительного числа

, зависящего от

.

Обозначения:

lim f (x, y) A

или

lim f ( M ) A .

x x

M

M

0

0

y y

0

Пример

1.

Пользуясь

определением

предела,

проверить,

что

2

2

1

lim

x

4 y

sin

0 .

2

2

x

y

x 0

y 0

Решение. Введем обозначения: пусть точка

M ( x;

y) ,

M 0

( x0

;

y0 ) , тогда

M M 0

x

2

y

2

. Зададим

0

, тогда при

M M 0

x

2

y

2

f ( M )

A

x

2

4 y

2

sin

1

0

x

2

4 y

2

sin

1

2

y

2

x

2

y

2

x

x

2

4 y

2

4x

2

4 y

2

2

x

2

y

2

2 ,

если выбрать

, т.е. lim f ( M ) 0 .



2

M

0

суперпозиции. Ее областью

определения считается множество всех тех

переменных x1 , x2 ,..., xn , при

которых формула, задающая функцию, имеет

y

не имеет определенного предела при произвольном стремлении точки

x

M ( x; y) к точке

M 0 ( 0; 0) . Так, если

M M 0 вдоль различных прямых

y k x , то

y

k ,

т.е. предел зависит от углового коэффициента прямой, по

x

которой движется точка M .



Пусть дана функция двух переменных

z f ( x, y) . Функция

приращением) функции

z f ( x, y) , соответствующим приращениям

x

и

y ее аргументов.

Частным приращением функции

z

по переменной x называется

приращение этой функции, соответствующее приращению

x

аргумента

x :

x z f ( x x, y ) f ( x, y ) .

Аналогично, y z f ( x, y y ) f ( x, y )

называется

частным

приращением функции z по переменной y .

При фиксированном значении переменной

y

функция

z f ( x, y)

становится функцией одной переменной

x

и,

согласно определению

по

x

от функции

z f ( x, y)

является функция переменных

x

и y ,

z

2 z

z

z

2 z

z

f

2

f

;

;

x

xx

xx

y x

xy

xy

x

x

y

x

z

2

z

z

2

z

z yx

f yx ;

2

z yy

f yy .

x

y

x y

y

y

y

частные производные

z

и

z

являются смешанными частными

xy

yx

x y

x y

2

f xx ( f x ) x (e

y) x e

y

;

f

( f )

(ex y y)

ex y x y ex y ex y ( x y 1) ;

xy

x y

y

9