Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

7804

.pdf

Скачиваний:

Добавлен:

23.11.2023

Размер:

1.23 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

z	lim		l	z	lim	f ( x	0
			l				0
l		l
l	l 0	l			x 0

Абсолютная величина производной

x, y

0y) f ( x0 , y0 )

по направлению

определяет

величину скорости изменения функции z в точке, характер этого изменения (возрастание, убывание).

Производная функции z f ( x, y) в точке M 0 ( x

вектора l cos ; cos вычисляется по формуле:

а знак производной –

0 ; y0 )

по направлению

z	z			cos z
	z			cos z
l	x	M	0	y	M 0
		M
	M
	M
	0

cos

Аналогично определяется производная по направлению для функции трех и более переменных.

Заметим, что производная по направлению представляет собой линейную комбинацию частных производных, а направляющие косинусы являются величинами (так называемыми “весовыми множителями”), показывающими вклад соответствующей частной производной в производную по направлению. Фактически, частные производные – это частные случаи производной по направлению.

Пример. Найти производную функции

u x	2	arctg ( y z)

в точке


M 2;1;1 по направлению вектора l	3 j	4 k .
Решение. Производная функции		u f ( x, y, z)	в точке	M
	;cos вычисляется по формуле:
направлению вектора l cos ; cos	;cos вычисляется по формуле:

по

		u																		cos .

		l		ux	M	cos u y							M	cos uz				M
		l											M

				M
Найдем частные производные и их значения в точке																	M			2;1;1 :
						2 x ,				u		M		2 2 4		,
					ux	2 x ,				x		M				,
					1				,						1							1	,

		u y						2		u y		M							2			5
				1 ( y z)				2						1 ( 1 1)					2


		u			1				,	u					1							1	.
												M
								2											2
		z		1 ( y z)				2		z				1 ( 1 1)					2			5
				1 ( y z)										1 ( 1 1)								5

Вычислим направляющие косинусы вектора l															:
											0							3						4
	32		( 4)2		5	,	cos				0		0 ,		cos			3		,	cos			4
l	32		( 4)2		5	,	cos				5		0 ,		cos			5		,	cos			5
											5							5						5

Подставим полученное в формулу производной по направлению:

u		4 0	1	3	1	4	3	4	1	.
		4 0								.
l	M		5	5	5	5	25	25	25
l	M



§10. Градиент

M 0

Пусть

( x	0	; y	0

)

функция

z f ( x, y)

определена в некоторой окрестности точки

Градиентом

grad z

функции

z f ( x, y)

вточке

M	0	( x	; y	)
	0	0	0

называется вектор, производных в точке

координатами которого

M 0	( x0	; y0 ) , т.е. grad z
		M

являются
	z
	x
		M
0		0
0

;

значения частных

	.
z y	.
	M
	0

M M

Аналогично находятся градиенты функции трех и более переменных.

Пример 1. Вычислить градиент функции					z 5 x	2	y 3 x y	3	в точке
Пример 1. Вычислить градиент функции					z 5 x		y 3 x y		в точке
2;1 .
Решение. Найдем частные			производные		и их		значения		в точке
2;1 :
z	10 xy 1,	z		10 ( 2) 1 1 21,
z	10 xy 1,	z		10 ( 2) 1 1 21,
x		x	( 2;1)
		x	( 2;1)

Тогда

z	5 x2 3y2 ,
y
grad z	21; 23 .
( 2;1)

z
y	( 2;1)
	( 2;1)

5 ( 2)	2	2
5 ( 2)		3 1



Пример 2. Вычислить градиент функции

u	x
u	yz	2
		2

вточке

	1	;	1	;	1
M	2		2		3	.

Решение. Так как задана функция u							трех переменных		x , y и z , то ее
градиентом в	точке	M	является			вектор в трехмерном			пространстве с
координатами	grad u							. Найдем частные производные
		ux		M	; u y	; uz	M
		M				M

и их значения в точке				M
	u				1
	u
	x			y z
				y z
		x			,

u y		2		2
	y	2	z	2
	y		z
		2 x			,

uz		y z		3
				3

Следовательно,	grad u				M
Следовательно,	grad u

	1	;	1	;	1		:
		;		;			:
	2		2		3
	,							1				3			2 ,

2			ux	M							2
2				M	(1		2)	(1		3)	2
					(1		2)	(1		3)
	u							1							3	2
	u														3	2
		y	M			2 (1		2)	2	(1		3)		2
			M						2					2

								2						6		3 .

	uz		M			2 (1		2)		(1	3)		3
			M										3

3			2 ; 3			2 ; 6		3	.



Пример 3. Вычислить угол между градиентами функций

	1		1		1		x			2		2		2
M		;		;		, если u			, v x		y		6z		.
								2
	2		2		3		yz
	2		2		3		yz

и v в точке

Решение. Найдем частные производные функции							v	и их
	1	;	1	;	1	:
точке M	2	;	2	;	3	:
	2		2		3

											2	,
					vx 2 x ,			vx	M		2	,
									M
												2	,
					vy 2 y ,			vy	M			2	,
									M
			v			v				1
				12 z ,			M	12		1		4 3 .
				12 z ,				12				4 3 .
			z			z					3
											3
Тогда,	grad v		2 ;		2 ; 4	3	;	grad u					3	2 ; 3	2 ;
		M									M

значения в

3 (см.

пример 2). По формуле косинуса угла между двумя векторами получаем:

cos	grad u grad v		3	2	2 3 2	2 6	3 4	3	84		7	13
	grad u	grad v		18 18 108		2	2 48		12 2	13		26

Следовательно,

arccos

713 26



Связь между градиентом и производной по направлению

1. Производная

функции по направлению равна скалярному

произведению

направленияl

вектора градиента

cos ; cos , т.е.

grad z

на единичный вектор этого

		z
		l	grad z l .
		l
2. Производная	z	функции по направлению
2. Производная	l	функции по направлению
	l

градиента на направление единичного вектора l , т.е.

z	пр		grad z	grad z	cos
l	пр		grad z	grad z	cos

		l
		l

есть проекция вектора


где	– угол между векторами	grad z и l .

3. Производная функции по направлению вектора вектору градиента, равна нулю:

z
z	0 , если l	grad z .
l

, перпендикулярного

Свойства градиента

1. Градиент функции в данной точке характеризует направление максимальной скорости изменения функции в этой точке, при этом модуль вектора градиента равен максимальному (минимальному) значению

производной

по направлению градиента (в направлении,

противоположном вектору градиента) в данной точке:

		z

		l			grad z					, если l			grad z								,
		l
	z

	l				grad z					, если l				grad z .
	l
2. Градиент дифференцируемой функции z f ( x, y)																									перпендикулярен
линии уровня, проходящей через точку											M 0		( x0				; y0 ) , если величина градиента
в этой точке отлична от нуля.
Пример 4. Найти производную функции																			z ln ( x						2	y	2	)	в точке
Пример 4. Найти производную функции																			z ln ( x							y		)	в точке
M 3; 4 в направлении вектора градиента функции.
Решение. Вычислим вектор градиента функции																				z	в точке M						:
				2 x				,									2 3						6	,
			2				2								2					2
zx			2				2		zx ( 3; 4)						2					2		25
	x			y									3				( 4)					25
	x			y									3				( 4)
			2 y					,						2 ( 4)									8		,
		2				2				( 3; 4)				2					2
z y		2				2			zx	( 3; 4)				2					2				25
	x			y								3				( 4)							25
	x			y								3				( 4)
					grad z							6	;				8
					grad z								;					.
									(3; 4)			25					25

Тогда

	grad z
(3; 4)	(3; 4)
(3; 4)

6	2	8	2

25		25

2 5



§11. Касательная плоскость и нормаль к поверхности


Пусть	z f ( x, y)	– дифференцируемая функция
в точке M 0 ( x0 ; y0 ) .		Графиком функции z является
некоторая	поверхность S		в пространстве, точка
M 0 ( x0 ; y0 ; z0 ) , где z0 f ( x0			, y0 ) , принадлежит этой

поверхности. Пересечем поверхность x x0 и y y0 (рис. 8).

плоскостями

Рис. 8
Пересечением плоскости x x0 и поверхности S является некоторая
линия, уравнение которой z f ( x0 , y) . К этой линии на плоскости	x x0 в
23

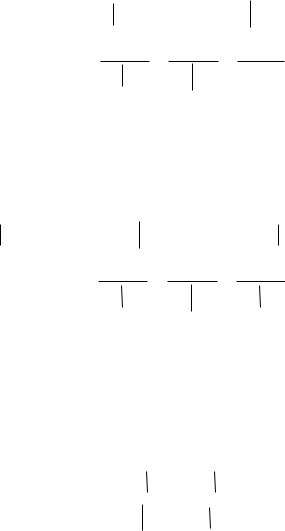
точке

M 0

может быть

проведена касательная

l 1 ,

так как

функция

f ( x0

, y)

дифференцируема в точке

y y0

(в

силу того, что точка

M 0

( x0

;

; z0 )

принадлежит данной

линии

функция

z f ( x, y)

дифференцируема в точке M 0 ( x0 ; y0 ) ).

Аналогично рассуждая для сечения поверхности S

плоскостью

y y0 ,

получим, что к линии z

f ( x, y0 ) на плоскости

y y0

в точке

M 0

может

быть проведена касательная l 2 . Прямые

l 1 и

l 2

определяют плоскость,

которая называется касательной плоскостью к поверхности

в точке

M 0

, точка

M 0 – точка касания.

Заметим, что касательная плоскость к поверхности в точке M 0

содержит

касательные ко всем кривым, принадлежащим данной поверхности и проходящим через точку M 0 .

Прямая, проходящая через точку M 0 поверхности S перпендикулярно к

касательной плоскости, проведенной в этой точке, называется нормалью к поверхности S в точке M 0 .

Если поверхность S задана явно уравнением z f ( x, y) и функция z f ( x, y) дифференцируема в точке M 0 ( x0 ; y0 ) , то уравнения касательной плоскости и нормали к этой поверхности в точке M 0 ( x0 ; y0 ; z0 ) имеют вид

z z	0
	0

f		( x x	0	) f	( y
x	M 0		0	y	M
					0

x x		0	y y		0	z z	0


f	M		f			1
x	M	0	y	M
				0

y	0	)
	0


соответственно.
Если поверхность		S	задана неявно уравнением F( x, y, z
F( x, y, z ) 0	дифференцируема в точке			M 0 ( x0 ; y0 ; z0 ) ,

касательной плоскости и нормали к этой поверхности в точке имеют вид

F		( x x	0	) F		( y y	0	) F	( z z	0	)
x	M 0		0	y	M	0	0	z	M 0	0
	M 0				M				M 0

x x		0	y y			0	z z		0


F	M		F				F	M
x	M	0	y	M	0		z	M	0
		0		M					0

) 0	и функция
то	уравнения
M 0 ( x0 ; y0 ; z0 )
0 ,

соответственно.

Пример 1. Написать уравнения касательной плоскости и нормали к

поверхности x2 4 y 2 9z 2		33 0			в точке M 0 3; 2;1 .
Решение.	Поверхность				задана		неявно.	Здесь
F ( x, y, z ) x2	4 y2 9z 2 33 . Найдем частные производные этой функции
и вычислим их значения в точке M 0 3; 2;1 :
	Fx 2 x ,	Fx M		0	2 x M	2 ( 3) 6 ,
				0		0
	Fy 8 y ,	Fy M		8y M 0		8 ( 2) 16 ,
			0
					24

18 z ,

18 z

18 .

Тогда уравнение касательной плоскости в точке

M 0 имеет вид:

6 ( x 3) 16 ( y 2) 18 ( z 1) 0,

3(x 3) 8( y 2) 9(z 1) 0 ,

3x 8y 9 z 34 0

и уравнение нормали:

x 3

y 2

z 1

или

x 3

y 2

z 1

Пример 2. Написать уравнения касательной плоскости

поверхности z 4 x

3 xy

в точке

M 0 2;1; 1 .

Решение. Поверхность задана явно. Найдем частные

функции z f ( x, y)

и вычислим их значения в точке M 0

2;1;

12 x

12 ( 2)

48,

f x

2 y ,

2 y

2 .

f y

M 0



и нормали к

производные

1 :

Тогда уравнение касательной плоскости в точке			M 0	имеет вид:
z 1 48 ( x 2) 2 ( y 1)
или
48 x 2y z 97 0
и уравнение нормали:
x 2	y 1	z 1
48	2	1
48	2	1
или
x 2	y 1	z 1	.
48	2	1	.
48	2	1



§12. Экстремумы функции двух переменных

Пусть функция z f ( x, y) определена в некоторой окрестности точки

M 0 ( x0 ; y0 ) .

Точка	M 0	( x0 ; y0
функции	z f ( x, y) ,
такая, что	для	всех

)	называется	точкой максимума	(минимума)
если существует -окрестность точки			M 0 ( x0 ; y0 )
точек из этой		окрестности, отличных от точки

M ( f

0	( x	0	;

( x, y)

y	0	)
	0
		f

( x	0	,
	0

y	0	)
	0

выполняется неравенство

f ( x, y)	f ( x	0	, y	0	)
		0		0

Точки максимума и минимума функции называются точками экстремума.

Значение функции в точке максимума (минимума) называется

максимумом (минимумом) функции. Максимум и минимум функции называются ее экстремумами.

Заметим, что экстремумы функции имеют локальный характер, так как в силу определения максимальное и минимальное значения функции рассматриваются лишь в некоторой окрестности точки M 0 ( x0 ; y0 ) . Так,

функция может либо иметь несколько экстремумов, либо не иметь ни одного.

Теорема	(необходимое условие точки экстремума). Пусть точка
M 0 ( x0 ; y0 ) –	точка экстремума дифференцируемой функции z f ( x, y) .

Тогда частные производные функции					z f ( x, y) в этой точке равны нулю,
т.е.				0 .
т.е.	f x	M	0 и f y	0 .
		M	0	M
				0
	С геометрической точки зрения равенство нулю частных производных
	и		означает,	что касательная плоскость к поверхности, являющейся
f x	и	f y	означает,	что касательная плоскость к поверхности, являющейся

графиком функции

( x,

, в точке экстремума параллельна плоскости

O xy

вид:

, так

z z0 z

как уравнение касательной плоскости в точке экстремума имеет

Заметим, что функция может иметь экстремум в точках, в которых хотя бы одна из частных производных

не существует. Например, функция	z 2	x	2	y	2

имеет максимум в точке

O (0; 0)

y	этой точке частных производных.

(рис. 9), но не имеет в

Рис. 9

Точки, в которых частные производные первого порядка равны нулю или хотя бы одна из частных производных не существует, называются

критическими точками функции z f ( x, y) .

Точки, т.е. f x 0 z f ( x, y) .

в которых

и		0
	f y

частные производные первого порядка равны нулю, , называют стационарными точками функции

Если функция достигает экстремума в какой-либо точке, то эта точка является критической точкой (но не наоборот!). Не всякая критическая точка будет являться точкой экстремума функции. Таким образом, каждую найденную критическую точку функции надо дополнительно исследовать.

Теорема (достаточное условие точки экстремума). Пусть функция z f ( x, y) имеет в стационарной точке M 0 ( x0 ; y0 ) и в некоторой ее

окрестности непрерывные частные производные до второго порядка включительно. Обозначим значения частных производных второго порядка

этой		функции		в точке		M 0 ( x0 ; y0 )	через
		B ,			C , а также обозначим
f xy	M		f yy	M
		0			0

C , т.е.

f
xx
	M
	0

			A	B	AC B	2	.
						2
			B	C
			B	C
Тогда:
1) если	0 ,	то функция		z f ( x, y)		в		точке		M 0	( x0 ;
экстремум: максимум, если A 0 ;				минимум, если				A 0	;
2) если	0 ,	то функция		z f ( x, y) в точке					M 0	( x0	; y0 )
экстремума;
3) если	0 , то в точке M 0 ( x0 ; y0 ) экстремум может быть,

не быть. В этом случае требуются дополнительные исследования.

y0 )

имеет

не имеет

а может и

Пример 1. Найти экстремумы функции z x3 y3 3 xy .

Решение. Найдем критические точки функции. Для этого получим сначала частные производные первого порядка:

Точек,

или
	f y

f 3 x2	3y ,	f 3y2	3 x .
x		y

вкоторых не существует хотя бы одна из частных производных f x

,нет. Найдем стационарные точки функции, пользуясь необходимыми

условиями точек экстремума:
	f 0,		2
	f 0,	3( x		y) 0,
	x	3( x		y) 0,
	f 0,	т.е.	2
		3( y	2	x) 0.

	y

Решая систему уравнений, получаем две точки: M1 ( 0; 0)

M 2

( 1;1)

Исследуем каждую из полученных критических точек. Для этого найдем частные производные второго порядка и составим для каждой критической точки соответствующий определитель :

6 x ,

6 y .

Для критической точки M1

( 0; 0)

имеем:

0 ,

0 .

A1 f xx

B1 f xy

C 1 f yy

В этом случае

		A

1		B
		B

1 1

B C

1		0

		3
1

3 0

следовательно, в точке

( 0; 0)

функция z экстремума не имеет.

Для второй критической точки M 2

( 1;1)

имеем:

6 ,

6 .

xx M 2

xy M 2

M 2

Тогда	2	A	2	B	2	6	3	36 9 27

		B		C		3	6
			2		2

функция z имеет экстремум. Так как A 2 0 , то

zmin f ( M 2 ) 1.

0	, значит, в точке M 2 ( 1;1)

M 2 ( 1;1) – точка минимума и



Пример 2. Найти экстремумы функции z x	4	y	3	3 x	2	y .

Решение. Найдем частные производные первого порядка:

	4 x	3	6 xy ,		3y	2	3 x	2	.
f x				f y

Точек, в которых не существует хотя бы одна из частных производных

или		, нет. Найдем стационарные точки функции:
	f y


f 0,		2 x ( 2 x		2	3y) 0,


x	т.е.
f 0,		3( y	2	x		2	) 0.


y

f x

Решая

M 3		3
M 3		2
		2

систему уравнений, получаем три точки:

;	3
;	2	.
	2

M	( 0;
1

M 2	3	;	3
	2		2

f	12 x
	2
xx

Для критической точки

		0	,
A1 f xx	M	0	,
	1

6 y ,
M	1	( 0;
	1
	B
		1

	f		6
		xy
0)	имеем:
f			0
xy		M
			1

f yy

C
1

f yy

y .

В этом случае 1							A	1			B	1					0		0		0 , значит, в точке M1 ( 0; 0) требуется
								1				1
							B			C							0		0
							B	1		C		1					0		0
провести				дополнительное										исследование.									Возьмем					точки	из				окрестности
точки M1 ( 0; 0)						с ординатами, равными нулю,																					тогда	z f ( x,0) x							4	0		при
точки M1 ( 0; 0)						с ординатами, равными нулю,																					тогда	z f ( x,0) x								0		при
x 0	,	y 0 . Затем рассмотрим точки из окрестности M1																											( 0; 0) такие,									что
x 0	,	y 0			. Для таких точек получим: z f ( 0, y) y3 0 . Это означает, что
в окрестности точки							M1			( 0; 0)						функция принимает как положительные, так и
отрицательные значения. Поэтому в точке																							M1 ( 0; 0)					функция экстремума не
имеет.
Для второй критической точки																						3		;	3
Для второй критической точки																				M 2		2		;	2		имеем:
																						2			2
				f							3		2						3							f						3
		A				12									6					18,			B					6						9 ,
		A				12									6					18,			B					6						9 ,
			2		xx M 2						2								2						2		xy M 2					2
													C 2								6		3				9 .

																		f yy					2
																				M 2			2
Тогда 2					A 2	B 2			18					9	162 81 81 0 , значит, в точке																	M 2					3	;	3
					B 2	C 2				9				9
																																					2		2
																																					2		2
																														3			3
функция				z	имеет		экстремум.											Так как				A 2					0 , то	M 2			;					– точка
функция				z	имеет		экстремум.											Так как				A 2					0 , то	M 2			;					– точка
																														2			2

минимума и

	3	4	3	3		3	2	3	81
	3		3			3		3	81
zmin f ( M 2 )					3			2	16
	2		2			2		2	16

Для третьей критической точки								M 3	3	;	3	имеем:
Для третьей критической точки								M 3	2	;	2	имеем:
									2		2
				3	2		3
				3			3	18 ,
			12			6
A3 f xx	M		12	2		6	2				B 3 f xy		M 3
	M	3

									6	3	9 .

						C 3 f yy		M 3		2
								M 3		2
Тогда	3	A	3	B	3	18	9	162 81 81 0				,
			3		3
		B		C		9	9
		B	3	C	3	9	9
			3		3

27	3	27
8		8

	6	3
		2

значит,

27 16

точке

M 3	3	;	3	функция имеет экстремум. Так как
M 3	2	;	2	функция имеет экстремум. Так как
	2		2
минимума и
					3	4	3	3
					3		3
				zmin f ( M 3 )	2		2	3
					2		2

A	3
	3

0	,
2

то

	3
	2
	2

M 3
M 3

– точка



<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023152.26 Кб0780.pdf
#
23.11.20231.23 Mб07800.pdf
#
23.11.20231.23 Mб07801.pdf
#
23.11.20231.23 Mб07802.pdf
#
23.11.20231.23 Mб07803.pdf
#
23.11.20231.23 Mб07804.pdf
#
23.11.20231.23 Mб07805.pdf
#
23.11.20231.23 Mб07806.pdf
#
23.11.20231.23 Mб07807.pdf
#
23.11.20231.23 Mб07808.pdf
#
23.11.20231.23 Mб07809.pdf