7759

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

x = arcsin t

.pdf

Скачиваний:

Добавлен:

23.11.2023

Размер:

1.22 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

5.275. В круг радиуса R

вписан квадрат, в квадрат вписан круг, в этот круг

опять вписан квадрат и так

n раз. Найти предел суммы площадей всех

кругов и площадей всех квадратов при n → ∞ .

§4.

Сравнение бесконечно малых

В задачах

5.276-5.287

определить порядок малости функции

β (x)

относительно x

при x → 0 :

β (x ) = 1 − cos x .

β (x) = x3 + 100x 2 .

β (x) = 3

−

5.276.

5.277.

5.278.

5.279.

β (x) =

x(x +

)

5.280.

β (x ) = sin x − tg x .

5.281.

β (x) = 3sin3 x − x4 .

1 +

β (x) = e

−1 .

β (x) = esin x − 1.

β (x) = e x2 − cos x .

5.282.

5.283.

5.284.

β (x) = sin(

−

5.286. β (x) = cos x − 3

5.285.

x + 2

cos x

5.287.

β (x ) = arcsin x .

1 − x

При x → 1 функции

y =

и y = 1 −

5.288.

бесконечно малые.

1 + x

Какая из них более высокого порядка малости ?

5.289. Убедиться в том что при

x → 1 бесконечно малые 1 − x

1 − 3

будут одного порядка малости. Будут ли они эквивалентны ?

5.290. Доказать, что при

x → 0 :

1) sin mx ≈ mx ;

2) tg mx ≈ mx ;

3) 3

− 1 ≈

x ;

4) ln(1 + x ) ≈ x .

1 + x

5.291. Какой из функций

x 2 ,

, x3 ,

x 2

при

x → 0

эквивалентна бесконечно малая

1+ x3

5.292. Какой из функций

2x2 , x3 , x2 , 2x3 ,3x

при

x → 0

эквивалентна

бесконечно малая

tg 2x − 2 tg x

5.293. Исходя из эквивалентности при x → 0

− 1

функций

1 + x

вычислить приближённо

105

§5. Непрерывность функции. Точки разрыва

Найти точки разрыва и построить графики функций:

5.294.	y =	3	.	5.295. y = tg x .	5.296. y =	1	.
						− x 2
		x			1

5.297.	y =		x +1			.		5.298.	y = x +		x −	1		.	5.299. y = 2 -	x	.
			x +1								x −	1
			x +1								x -	1


																x
									2
5.300.	y =	x3		+	x		.	5.301.	y =	4 − x			.
		x3		+	x					3
				x

			2							4x − x

В задачах 5.302 - 5.304 найти точки разрыва функций:

1			1				x
5.302. y = 1 − 2		.	5.303. y = 2		.	5.304. y = 3		.
	x			x−2			x + 3

В задачах 5.305-5.306 построить графики функций и указать точки разрыва. Какие из условий непрерывности в них выполнены и какие не выполнены?

	2 ,				x = 0, x = ±2							x				x ¹ 2
	4 − x		2	,	0 <					x	< 2 .			,	при		.
			2										2	,	при
5.305. y =												5.306. y =	2			x = 2
									> 2				0 ,		при	x = 2
	4 ,						x		> 2				0 ,
5.307. Исследовать функцию на непрерывность
	2				1							π
-		arctg						, x < -
-	π	arctg			x +	π		, x < -				2
					x +	2
						2
f (x) =	ectg x ,				- π			£ x < 0 .
				1		2
				1		,			x > 0

		1 - ln x
		1 - ln x

При каком значении a функции непрерывны на всей числовой оси:


		2	- 5x + 6,	x ¹ 2 .		x − 1,			x ≤ 1
5.308.	f (x) = x		- 5x + 6,	x ¹ 2 .	5.309.	f (x) =	2	− 2, x > 1		.
	a ,			x = 2
						ax

Глава 6

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

§1. Производная функция

В задачах 6.1-6.9, пользуясь определением производной, найти

производные следующих функций:
6.1. y = 3x + 5.	6.2. y = x2 - 2x .	6.3. y = x3 .

			y =	1			y =	1
6.4.	y = x .	6.5.			.	6.6.				.
								x	2
				x
6.7.	y = sin x .	6.8.	y = ln x .			6.9.	y = cos x .

В задачах 6.10-6.27, пользуясь формулами и правилами дифференцирования, найти производные следующих функций:

6.10. y = x2 - 2 + 3 .

3 x

6.13.	s =		2t4
									.
		t2 + 3t +1
	y = x2 (					+ tg x) .
6.16.					x
6.19.	y =10x × log x .
				7
	y =		e x - ln x
6.22.								.

			e x + ln x
6.25.	y =		2x	- 2			.

arcsin x

3x3

6.11. y =

. 6.12. y =

5 x2

3 x5

3 - x

6.14.	y =	5	+	ln x	.
		sin x
				x 2

6.17.y = x3 × 3x + ctg3 .

6.20.y = x × (log5 x - 1).


6.23.	y =		arctg x	.

		arcctg x
	y =		arccos x
6.26.					.
			e x + 3x

6.15. y =					x		-			x	3		.
		- cos x

	3						7
6.18.	y = ex × arcsin x .
	y =		3x2			+ ctg x
6.21.												.
			1			- 3

								x
6.24.	y =				arccos x					.

					ln x
6.27.	y =			arcctg x					.

					log2 x

В задачах 6.28-6.69 найти производные сложных функций:

	y = sin4x .															y = tg 4 x .																	y = arcsin
6.28.	y = sin4x .														6.29.	y = tg 4 x .																6.30.	y = arcsin										x .
																																	y = 4											.
																y =														.							(x2 - 1)5
	y = 5 × 5								.										1 + 4x − x2
6.31.	y = 5 × 5					4x + 3			.						6.32.				1 + 4x − x2													6.33.
																																	y =		x										.
																																							49 − x 2
	y = 3 2x3 +1 + 4														6.35. y = x ×														+			. 6.36.
6.34.													3	.								1 + 5x									ln 2
6.34.													3	.								1 + 5x									ln 2
																																	2
							2																		2		-
6.37.	y =						2					.			6.38.	y = 2 arctg							x		2			3	.			6.39.	y = 3 (1 + sin 2 x)5 .


				1 + x + x						3

																										6
																										6
6.40.	y =			1 - x3						.					6.41.	y =	lnsin3x									.						6.42.	y =						x				.
6.40.	y =	arcctge2 x								.					6.41.	y =	lncos4x									.						6.42.	y =	cos3 e2 x									.
		arcctge2 x															lncos4x																	cos3 e2 x
6.43.	y =				cos x						.				6.44.	y = e		1			.											6.45.	y = x			2		×10		1		.
																		ln x																						x
																		ln x																						x
	1			+ lnsin 3x
							x									y = 2x				2		× tg		4									y = x3 × ctg										2
6.46.	y = x		9		× 9			.							6.47.											.						6.48.														.
							ln x
							ln x																	x																	3x 2
																								x																	3x 2

		1
	y =	1							y =	1						6.51. y =			1 - sin x
6.49.				x .				6.50.		1					.					.

										arccos4 2x

		cos6 e		2														1 + cos x

	y =								y =							6.54. y = 2 × 3 x5 + 1 +					5		.
6.52.			arcsin2x		.			6.53.			x +
												x	.
												x	.
																						x
			2			x						1
			2			x						1				. 6.57. y = ln2	(3 9 − 5x ).
6.55.	y = ln			+ tg			.	6.56.	y = ln arctg
6.55.	y = ln			+ tg			.	6.56.	y = ln arctg						+ 1
			x3	2										x	+ 1

6.58.	y = arccos				1 − x2
	4
6.61.	y = e x 2 ctg			.
		3x
						2x		2
6.64.

	y = arcsin tg
			3
6.67.	y = arctg3		1				.


					x

.	6.59.	y = arctg 3 2 x .						6.60.	y = 3x arctgsin x .
		y = 2x		.					y = 5− x 2
	6.62.		x −1					6.63.			tg2					.
	6.62.		x −1					6.63.			tg2			x		.
	6.65. y = arccos			2x 2								3 - x						2
.							.	6.66.	y = arcctg								.
.							.	6.66.	y = arcctg			x					.
			1 + x		4							x	- 5
									y = log	1 - e−x					.
	6.68.	y = ln	1 + tg x			.		6.69.


			1 − ctg x						6		ex
			1 − ctg x								ex

В задачах 6.70-6.81 найти производные неявно заданных функций:

6.70.

xy = y3 − 2x2 .

6.71.

x 2

y 2

= 1 .

6.72. x2 − 5y2 + 4xy − 1 = 0 .

a 2

6.73.

y = 1 + xe y .

6.74.

x 2 + e xy

= y 2 .

6.75.

y = sin x + cos(x - y) .

x + y = ex + e y .

ln y = arcsin

6.76.

6.77.

6.78.

+ e x − 3

= 0 .

6.79.

2 xy = x 2 − y 2 .

6.80.

y = cos(2x + y) .

6.81.

sin(x × y) = x .

В задачах 6.82-6.85 найти производные неявно заданных функций в

указанных точках:

−

+ y

= 1

в точке ( 0 ; 0 ) .

6.82.

;

в точке

. 6.83. x = y + sin y

6.84. x2 + xy + y2 = 3 в точке (0 ; −

). 6.85. (x − 1)y = ye y

− xe x в точке (1;1) .

В задачах 6.86-6.94 найти производные функций, используя метод

логарифмического дифференцирования:

6.86.

y = x x .

6.87. y = (sin x)cos x .

6.88.

y = xln x .

x x

sin x

arcsin x

6.89.

y =

6.90.

y = (x2 + 1)

6.91.

y = x

1 + x

y = (x +

1)3 × 4

x - 2

6.92.

y = x

1 − x

6.93.

y = x arcsin

6.94.

1 + x

5 (x - 3)2

задачах

6.95-6.106 найти

производные

функций,

заданных

параметрически :

x = t 2 + 2

6.95.y = 1 t3 − t .3

t + 1

x =

6.98.

t - 1 .

y =

1 + t

x =

1 + t

6.101.

3at

2 .

y =

1 + t

x =

+ 1

6.104.

t × e

y =

6.96.	x = e− 3t		.
6.96.			.
	y = e2t
6.99.	x = a cos3 t
6.99.			.
	y = a sin		3 t
		t

6.102.		2 .
6.102.	x = sin	2 .

	y = cost
	x = sin t - t
6.105.			- t	.
	y = cos t		- t

	x = a(t - sint)
6.97.						.
	y = a(1 - cost)
6.100.	x = et	sin t
6.100.		.
	y = et	cost
	x = arccos
	x = arccos			t
6.103.					.
6.103.			t − t 2		.
	y =		t − t 2
6.106.	x = ln(1 + t 2 )					.
6.106.						.
	y = t - arctg t

В задачах 6.107-6.122 найти производные указанного порядка от заданных функций:

6.107.	y = x3 + 2x2 − 4x ,								y ′′′ = ?
6.109.	y = x5 ,	y (5)			= ?
6.111.	y = ex 2	,	y ′′′ =			?
6.113.	y = (1 + x 2 )× arctg x ,								y′′ = ?
6.115.	y = tg(x + y ),					y′′ = ?
6.117.	s = 1 + te s ,			d 2s			= ?
				dt2

	x = a cost				d	3	y	= ?
6.119.			,

	y = bsin t				dx3

6.108.

y = ln x ,

y (4) = ?

6.110.

y = sin2 x ,

y (6) = ?

y = ln(x +

) ,

y′′ = ?

6.112.

1 + x2

6.114.

x3 − 3xy + y3 = 0 ,

y′′ = ?

6.116.

xy = e x + y ,

d 2 y

= ?

dx2

x = at2

2 x

= ?

6.118.

dy 2

y = bt

x = ln t

= ?

6.120.

-1

dx2

y = t

	x = a(ϕ − sinϕ )			d	2	y	= ?
6.121.		− cosϕ )	,

	y = a(1			dx2

§2. Дифференциал функции. Применение дифференциала в приближённых вычислениях

В задачах 6.123-6.125 найти приращение функции

f и её

дифференциал df

(используя определение дифференциала) :

6.123.

f (x) = x3

в точке

x = 0 ,

если

x = 0,3 .

6.124.

f (x) = 6x2 + x

в точке

x =1,

если

x = 0,01 .

6.125.

f (x) = x2 − 2x

в точке

x = 3 ,

если

x = −0,01 .

В задачах 6.126-6.127 найти

приращение функции

и её дифференциал

(используя формулу

′

dy = y dx ) :

6.126.

y =

в точке x = 4 ,

x = 0,41 .

если

6.127. y =

в точке x = 9

если

x = −0,01 .

В задачах 6.128-6.151 найти

дифференциалы следующих функций:

6.128.

6.131.

6.134.

6.137.

6.140.

6.143.

y = 2sin x .

	v =	1

		1 - u2 .
		1 - u2 .

y =	x									.
	x			49 − x2
				49 − x2
2
1					.
y = e
y = e		ln x
1						1

y = 3x			+						.

							22x
y =			1					.

	sin		3
	sin		3			2 x

6.129.	s =		gt 2			.				6.130. s = a cos (ω × t + ϕ 0 ).

		2
6.132.	ρ = a cos2 2ϕ .										6.133.		1				.
												y = x2 ×10
															x
6.135.	y = 2sin x .										6.136.	y = 10x×arcsin x .
		1													x
6.138.	y = e				× log5 x .						6.139.	y = x9 × 9						.
				x
														ln x
							π		x			y = arctg	3		1
6.141.	y = ln cos						4	+			. 6.142.								.

									2							x
	y =	1										y = log6	1 - e							− x
6.144.								.			6.145.										.
		3

		arctg					5x										e x

6.146.

6.149.

	π
y = ln sin		2	− x .

y = arctg 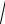x2 + 1.

6.147.	y = 4ln sin 2 x .			6.148.
	y = x2 × sin		.
6.150.	y = x2 × sin	x	.	6.151.

y =	1	ln	x − 5
			x + 5 .
2
y =		cos x

		− sin x .
1

6.152.		Вычислить			f (1,05 ) , если				f (x ) = e0,1x(1− x) .
6.153.		Вычислить приближенно :

				;	2)			;	3)			;	4)	3	7,98	;
1)		70					5				17
						(1,11)9 ;				(0,98)8 ;
5)	4	15,8	;		6)				7)				8)	e 0,1 ;
9)	e −0,03			;	10)	ln0,984 ;			11)	tg 45030′ ;			12)	tg 440 ;
13)	tg 460			;	14)	sin1,55;			15)	arcsin0,54 ;			16)	arctg 0,96 .

§3. Применение производной в геометрии и физике

В задачах 6.154-6.167 написать уравнения

касательной

и нормали к

кривым в заданной точке:

6.154.

f (x) = x 2 + 4 x − 3 ,

точка

(1 ; 2 ).

6.155.

f (x) = x 3 + 2 x 2 − 4 x − 3 , точка

(1 ; − 4 ).

6.156.

f (x) = x 2 − 2 x + 5

в точке с абсциссой

x 0 = 2 .

y = 3

абсциссой x 0 = 9 .

6.157.

x − 1

точке с

6.158.

y = ln x

в точке с абсциссой

x 0

= e .

6.159.

y = 2x − ln x

в точке с абсциссой

x 0

= 1 .

6.160.

y = arcsin

x − 1

в точке пересечения кривой с осью

OX .

6.161.

y = arccos3x

в точке пересечения кривой с осью OY .

6.162.

f (x) = tg 2x ,

в начале координат .

6.163.

y = x 3 + 2 x 2 − 1 в точке пересечения этой кривой с параболой y = 2 x 2 .

6.164.

y 4 = 3x3 в точке

( 3 ; 3 ) .

6.165.

x5 + y5 − 2 xy = 0

в точке

(1 ; 1 ) .

6.166.	x 4 + 2 y 3 − 3xy = 0				в точке (1 ; 1 ) .
6.167.	x2	−	y2	= 1	в точке M (− 9 ; − 8 ).
	9
		8
6.168.	Написать уравнение касательной					к кривой	y = x ln x в точке, в
которой нормаль к этой					кривой параллельна прямой		2x − 2 y + 3 = 0 .

В задачах 6.169-6.172 написать уравнения касательной и нормали к кривой, заданной параметрически :

x = t 2

6.169. 3 в точке с координатами ( 4 ; 8 ) .

y = t

6.170.

x = 2e t

точке,

соответствующей значению параметра t = 0 .

−t

y = e

x = sin t

при t = 0 .

6.171.

y = a

x = t − sin t

в точке , для которой t = π .

6.172.

− cos t

y = 1

6.173.

Написать уравнения касательных

к кривой

−

y 2

= 1 , которые

2x + 4 y − 3 = 0 .

перпендикулярны

прямой

6.174.

В какой точке касательная к кривой

y 2 = x 3

перпендикулярна

прямой 4x − 3y + 2 = 0

6.175. На линии

y =

найти точку, в которой касательная параллельна

оси абсцисс.

x 2 + 1

6.176. На кривой

y = x 3

найти точку, в которой касательная параллельна

биссектрисе первого координатного угла.

6.177. Найти углы, под которыми пересекаются данные линии:

1) y = x 2 и y = x 3 ;

2) y = x 2 и y = kx ;

3) x 2 + y 2 = 4 и x + 2 y = 2 .

6.178.

Точка движется прямолинейно

по

закону s = 3t 2 + t − 1 . Найти

скорость и ускорение точки для моментов времени t0 = 0 ,

t1 = 1 , t2 = 2

( s дается в метрах, t

- секундах).

6.179. Точка совершает колебательное движение по оси абсцисс по закону x = cosω t . Найти момент времени, когда скорость равна нулю. Чему в это время равно x ?

6.180. Количество электричества, протекшее через проводник, начиная с момента t = 0 , определяется формулой Q = 2t 2 + 3t + 1 . Найти силу тока в конце десятой секунды.

§4. Правило Лопиталя для вычисления пределов

В задачах 6.181-6.198 вычислить пределы, раскрыв неопределенности

вида 0 :

6.181.

6.184.

6.187.

6.190.

6.193.

6.196.

lim sin3x .

x→0 x

x − 1 lim .

x →1 3 x − 1

lim x − 1 . x →1 ln x

lim	tg x − sin x
	x − sin x .
x →0
	eax − ebx
lim		.

x →0	sin x

lim	x	4 − 16
			.

x → −2		x + 2

	lim				tg2x									lim				x7		− 1
6.182.						.							6.183.									.
6.182.						.							6.183.									.
	x→0 x													x →1 x9						− 1
6.185.	lim			1 + cos x					.				6.186.	lim		e x − 1					.
																e x − 1

	x →π				x − π									x→0 sin2x
6.188.	lim				1 − cos x			.					6.189.	lim			x − sin x							.
6.188.	lim							.					6.189.	lim										.
	x →0				x2									x →0						x3
	lim		x − arctg x											lim			1 − 2 sin x
			x − arctg x											lim
6.191.											.		6.192.	x →	π				cos 3x						.
6.191.					x3						.		6.192.		π										.
	x →0				x3										6
															6
6.194.	lim	x3 − 1					.						6.195. lim						x2 − 16							.
6.194.	lim						.						6.195. lim						2	− 5x +					4	.
	x→1 ln x													x→4 x					2	− 5x +					4
										5x					1 −					4sin			2 πx
6.197.	lim		1 + 5x − e									.	6.198.		1 −					4sin					6 .
			1 + 5x − e											lim

	x →0				sin	2	4x
	x →0					2													1 − x2
														x →1					1 − x2

В задачах 6.199-6.209 вычислить пределы, раскрыв неопределенности

∞ вида ∞ :

6.199.

1) lim

e x

2) lim

e x

x →+∞ x3

x →−∞ x

6.202

lim

x3 − 16

x →∞ x4 + 3x

6.205.

lim

lnsin5x

x →0 lnsin2x

6.208. lim x × e 2 .

x → ∞ x + e x

.	6.200. lim	ln x	. 6.201. lim	ln x	.


	x → ∞ x		x →0 ctg x

6. 203.

6.206.

6.209.

lim		tg x
lim		tg 3x .
x →	π	tg 3x .
x →	2
	2

lim ln(1 + e x )

x →∞ x

ctg(x − 1) lim ( − ) x →1 ln 1 x

		tg πx
6.204.	lim			2		.
				− x)
	x →1 ln(1
	lim		ln2 x
. 6.207.					.


	x →+∞ 100 x

В задачах 6.210-6.224 вычислить пределы, раскрыв неопределенности

вида			[0×¥]		,			[¥ - ¥]							,			1∞	,	00				∞0										сведением их к неопределенностям
вида		∞			,										,				,		,													сведением их к неопределенностям
0		∞
	,					путем алгебраических преобразований:
	,					путем алгебраических преобразований:
0			∞
6.210.			lim (π - x)× tg													x	.		6.211.						lim (1 - e2 x )× ctg x . 6.212.															lim x × ln x .
6.210.			lim (π - x)× tg														.		6.211.						lim (1 - e2 x )× ctg x . 6.212.															lim x × ln x .
			x→π												2										x → 0															x → 0
										1																		1									2							x				1
			lim x × e x										- 1 .															1						-			2							x		-		1
6.213.																		6.214. lim																				. 6.215.		lim
6.213.																		6.214. lim																				. 6.215.		lim
			x →∞																		x →	2 x						- 2 x 2 - 4												x →1 x				- 1 ln x

								1					-		1										lim x							x								lim x				sin x
6.216.			lim															.	6.217.													.						6.218.									.
6.216.			lim												x 2			.	6.217.													.						6.218.									.
			x →	0 x sin x											x 2										x → 0															x → 0
			lim (sin 2x)cos x																																3		x								1		ln x
6.219.			x → π														.		6.220.						lim				1				+				.	6.221.		lim		1 +					.
6.219.			x → π														.		6.220.						lim				1				+				.	6.221.		lim		1 +					.
				2																				x → ∞											x					x →∞					x
				1				tg x																											1 x											sin x
6.222.			lim					.											6.223.						lim (ln x ) .													6.224.		lim (ctg x )								.
6.222.			lim					.											6.223.						lim (ln x ) .													6.224.		lim (ctg x )								.
			x → 0 x																			x → ∞																		x → 0
					§5. Исследование функций и построение графиков
		В задачах 6.225-6.233 определить интервалы монотонности
следующих функций:
6.225.			y = x 2 .														6.226.				y = x 3 + 2 x - 5 .																	6.227.	y = 1 - x + 2 x 4 .
			y = 3						+			2		x .											1						.								y = x ln x .
6.228.							x2					2					6.229.				y =				1													6.230.
6.228.							x2										6.229.				y =																	6.230.
											3														x - 2
6.231.			y = 2 x 2 - ln x .														6.232.				y = x 2e− x .																	6.233.	y = x + cos x .
		В задачах 6.234-6.242 исследовать функцию на экстремум:
6.234.			y = x			3		.									6.235.				y =		1			x		4	-				2x			2	+ 3.	6.236.		y =	x2			+ 1			.
6.234.			y = x					.									6.235.				y =	4				x			-				2x				+ 3.	6.236.		y =			x				.
			y = 1 − ln x .																			4																					x
6.237.			y = 1 − ln x .														6.238.				y = x 2 − x2 .																	6.239.				2		x .
																																							y = x				e	1

								x
						2															y =			ln			2	x											y = x − arctg x .
6.240.						2					.						6.241.													.								6.242.
			y = x					- x
						3
						3
																										x

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.20231.22 Mб07754.pdf
#
23.11.20231.22 Mб17755.pdf
#
23.11.20231.22 Mб07756.pdf
#
23.11.20231.22 Mб07757.pdf
#
23.11.20231.22 Mб07758.pdf
#
23.11.20231.22 Mб07759.pdf
#
21.11.2023152.14 Кб0776.pdf
#
23.11.20231.22 Mб07760.pdf
#
23.11.20231.22 Mб07761.pdf
#
23.11.20231.22 Mб07762.pdf
#
23.11.20231.22 Mб07763.pdf