
7701
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
А.В.Бесклубная
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Учебно-методическое пособие по подготовке к лекционным и практическим занятиям
по дисциплине «Математический анализ» для обучающихся по направлению подготовки 38.03.01 Экономика,
направленность (профиль) Экономика предприятий и организаций
Нижний Новгород
2018
0
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
А.В.Бесклубная
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Учебно-методическое пособие по подготовке к лекционным и практическим занятиям
по дисциплине «Математический анализ» для обучающихся по направлению подготовки 38.03.01 Экономика,
направленность (профиль) Экономика предприятий и организаций
Нижний Новгород
2018
1
УДК 517.9
Бесклубная А.В. Математический анализ [Электронный ресурс]: учеб. -
метод. пос. /А.В.Бесклубная; Нижегор. гос. архитектур. - строит. ун-т.- Н. Новгород: ННГАСУ, 2018. – 65 с; ил. 1 электрон. опт. диск (CD-R).
Содержит методические рекомендации по подготовке к лекциям и практическим занятиям по основным разделам дисциплины «Математический анализ».
Предназначено для обучающихся в ННГАСУ по направлению подготовки 38.03.01 Экономика, направленность (профиль) Экономика предприятий и организаций.
Составитель Бесклубная А.В.
© А.В. Бесклубная, 2018 © ННГАСУ, 2018
2
§1 Функция одного переменного.
Основные понятия
Понятие функции является одним из главных понятий математики. С этим понятием часто встречаемся в природе, изучая различные процессы и явления.
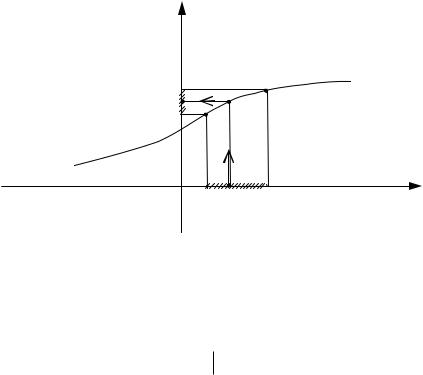
Пусть D – некоторое множество действительных чисел. Если каждому числу x D – поставлено в соответствие по какому-то правилу или закону f единственное действительное число y , то говорят, что на
множестве |
D задана функция |
одного переменного |
и |
обозначается: |
y f x . Число x D называется аргументом функции, |
y – значением |
|||
функции, множество D – областью определения функции, множество всех |
||||
значений |
y , которые соответствуют числам множества |
D – областью |
||
значений функции – E . (См. рис. 28) |
|
|
||
|
y |
|
|
|
|
E |
y f x |
||
|
y |
|
|
|
|
|
D |
|
|
|
0 |
x |
x |
|
|
|
Рис. 28 |
|
|
Графиком Г f функции |
y f x называется |
множество всех |
||
точек x, y плоскости xOy таких, что x D , а y f x , то есть
Г f x, y x D, y f x .
Далее будем задавать функцию одного переменного аналитически, то есть с помощью формулы. В этом случае под областью определения D функции понимают множество всех тех значений x , для которых данная формула имеет смысл.
3
Пример. Формула y x2 задает функцию y одного переменного x .
Поскольку данная формула имеет смысл при всех действительных значениях переменной x , то область определения D данной функции есть множество всех действительных чисел R , то есть D R. Так как квадрат действительного числа – число неотрицательное, то множество значений
E данной функции y x2 есть множество всех неотрицательных чисел,
то есть E y |
|
y 0 . |
Графиком функции |
y x2 является парабола в |
||||
|
||||||||
плоскости xOy с вершиной в точке O , |
ветви которой направлены в |
|||||||
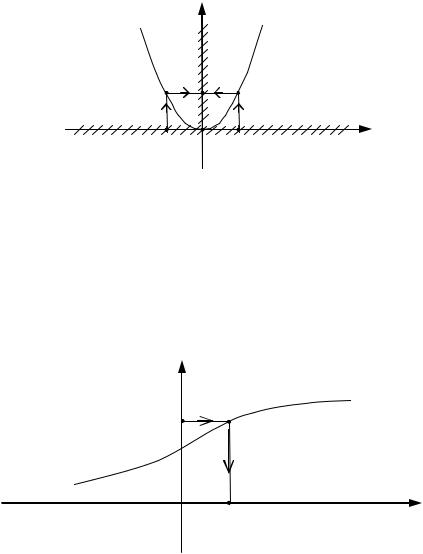
положительном направлении оси Oy . (См. рис. 29) |
|
|||||||
|
|
|
y |
|
|
|
y x2 |
|
|
|
|
|
E |
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
-1 |
0 |
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 29 |
|
|
|
Пусть задана функция |
y f x , |
x D , такая, что для x1 |
x2 , |
|||||
f x1 f x2 , то есть |
для любого y E |
найдется единственное x D |
||||||
такое, что f x y или |
x f 1 y . |
Тем самым определена функция |
f 1 , |
|||||
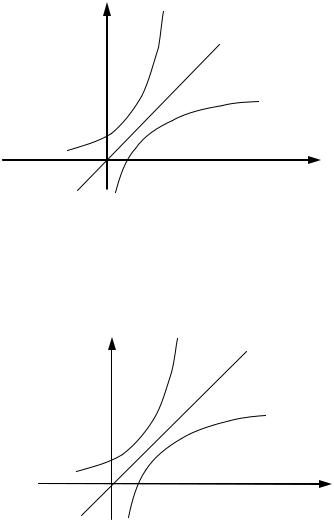
называемая функцией, обратной к функции f . (См. рис. 30)
y
y f x
y
0 |
x f 1 y |
x |
Рис. 30
4
Покажем как строим график обратной функции. Если для обратной функции обозначить аргумент через x , а функцию через y , то графики
функций и совпадают. Разница состоит лишь в том,
что для функции y f x ось Ox – ось абсцисс, а ось Oy – ось ординат,
а для функции x f 1 y роль осей меняется.
Если же обозначить аргумент обратной функции через x , а значение функции через y , то получается иной график. Именно, нужно перевести друг в друга оси Ox и Oy . Это делается с помощью отражения всей плоскости xOy относительно биссектрисы первого координатного угла, то есть прямой y x . При этом отражении график функции переходит в график обратной функции
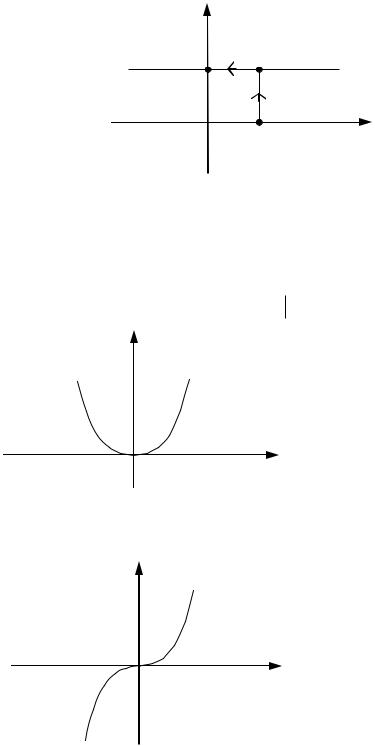
Итак, график обратной функции симметричен графику заданной функции относительно прямой y x . (См. рис.31)
y f 1 x
y x
y f x
0 |
Рис. 31 |
x |
|
|
Пример. Функция y ex является обратной функцией к функции y ln x. (См. рис. 32)
y |
y ex |
y x
y ln x
1
0 1 Рис. 32 x
5
Основные элементарные функции
Следующие шесть типов функции называются основными элементарными функциями:
I. Постоянная функция y C – функция, ставящая в соответствие каждому действительному числу x одно и то же число C . (См. рис. 33)
D R, E C .
y
y C
C
0 |
x |
x |
Рис. 33
II. Степенная функция y x .
а) – целое число.
Если – четное, то D R, E y y 0 .
y
y x ( - четное, целое)
0 |
x |
|
Рис. 34 |
Если – нечетное, то D R, E R. |
|
y |
y x ( - нечетное, целое) |
0 |
x |
Рис. 35
6
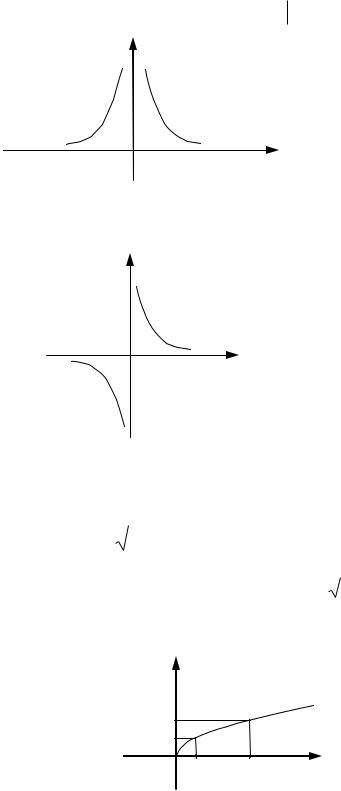
Графики функции y x ( – целое) показаны на рис. 36 и рис. 37
соответственно. |
|
– четное, D R \ 0 – множество всех |
В случае |
если |
действительных чисел, кроме нуля, E y y 0 .
y
y x ( - четное)
0 x
|
Рис. 36 |
В случае если – нечетное, D R \ 0 , E R \ 0 . |
|
y |
y x ( - нечетное) |
|
|
0 |
|
|
|
|
x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Рис. 37 |
|||||||||
б) – рациональное, то есть |
m |
, m, n , n 0 ; |
||||||||||||||||
n |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
||||
y x x |
|
n xm . |
|
|
|
|
|
|
|
|
|
|||||||
n |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
Пример графика функции y x |
|
|
или y |
x |
. (См. рис. 38). |
|||||||||||||
2 |
||||||||||||||||||
D x |
|
x 0 , E y |
|
y 0 . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
y x 2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|||||||||
0 1 |
4 |
|
|
x |
||||||||||||||
Рис. 38
7
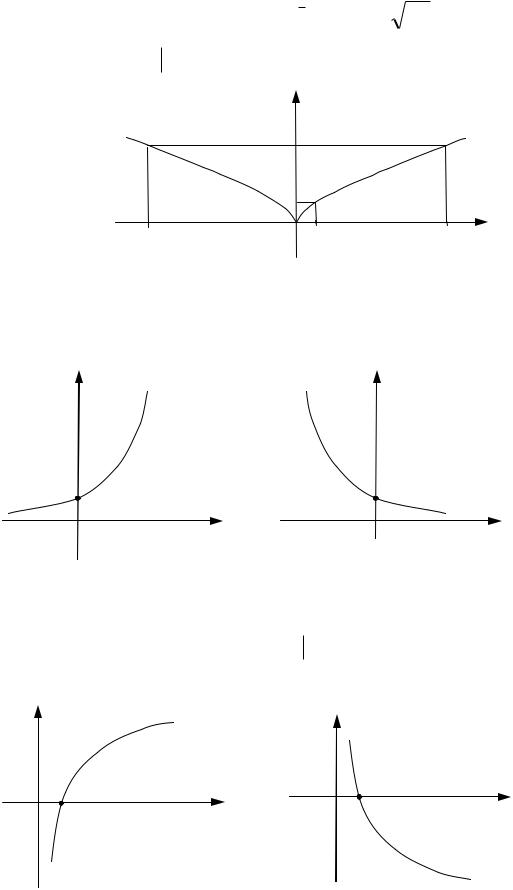
2
Пример графика функции y x3 или y 3 x2 .(См. рис.39).
D R , E y y 0 .
|
y |
|
|
|
2 |
|
|
|
|
|
y x 3 |
|
|
|
|
4 |
|
|
|
|
|
|
1 |
|
|
|
|
-8 |
|
0 |
1 |
8 |
x |
|
|
|
|
|
|
||
|
|
|
Рис. 39 |
|
|
|
III. Показательная функция |
|
|
|
|
|
|
y ax a 0, a 1 , |
D R , |
E : y 0 . |
|
|
|
|
y |
|
|
y |
|
|
|
y ax a 0 |
|
|
y ax 0 a 1 |
|||
1
0 |
x |
Рис. 40
1
0 |
x |
Рис. 41
IV. Логарифмическая функция |
|
y log a x a 0, a 1 , D x x 0 , |
E R |
y |
|
y |
y log a |
x 0 a 1 |
|
|
|||
|
|
|
||
y log a |
x a 1 |
|
1 |
|
|
|
|
|
|
0 1 |
x |
0 |
|
x |
|
|
|
Рис. 42 |
Рис. 43 |
8
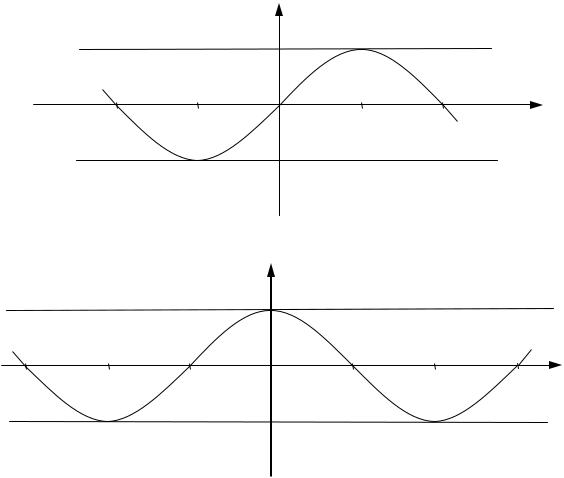
V. Тригонометрические функции
а) y sin x , D R , |
E 1;1 . |
|
y |
|
1 |
|
|
|
2 |
||
|
0 |
|
|
x |
|
|||
|
2 |
|
|
-1
Рис. 44
б) y cos x , D R , E 1;1 . y
|
3 |
|
|
|
2 |
|
2 |
1
0 |
|
|
3 x |
|
|
||||
|
2 |
|
2 |
|
-1
|
|
Рис. 45 |
|
|
|
|
|
|
|
в) y tg x , |
|
|
– множество всех |
|
D R \ |
n, n Z |
|
||
|
2 |
|
|
|
действительных чисел R , за исключением точек |
|
n , n , E R. |
||
|
|
|
2 |
|
9
