7527

УДК 625.712.02

Агеева В.В. / Гидравлика дорожных сооружений [Электронный ресурс]: учеб.

– метод. пос. / В.В. Агеева, А.К. Битюрин; Нижегор. гос. архитектур. - строит. ун-т – Н. Новгород: ННГАСУ, 2022 – 45 с.

Учебно-методическое пособие содержит курс лекций (включая рекомендации обучающимся по выполнению лабораторных работ, организации самостоятельной работы) по гидравлике дорожных сооружений, справочные данные, примеры расчетов и решения задач разделов, предусмотренных учебной программой, рассмотрено содержание и последовательность выполнения расчетно-графической работы, даны рекомендации и указания к выполнению лабораторных работ. В частности, определение критической глубины и критического уклона открытых потоков, гидравлический расчет сооружений для гашения энергии потоков, конструкции и гидравлических расчетов быстротоков, многоступенчатых перепадов, консольных водосбросов. Излагается методика гидравлического расчета водопропускных труб, являющихся наиболее распространенным типом искусственных сооружений в автомобильных и железных дорогах. Предназначено обучающимся в ННГАСУ по дисциплине «Гидравлика дорожных сооружений» по направлению подготовки 08.03.01 Строительство; направленность (профиль) Автомобильные дороги.

© В.В. Агеева, А.К. Битюрин

©ННГАСУ, 2022

4

Введение

Целью методических рекомендаций является углубление знаний, полученных при изучении материала дисциплины «Спецкурс гидравлики дорожных сооружений».

Минимум теоретического материала и методика решения конкретных задач позволит студентам достигать поставленной цели. Полученные знания необходимы будущим специалистам как на этапе проектирования дорог и конкретных дорожных сооружений, так и при строительстве и их эксплуатации. Кроме того, при возникновении негативных моментов в процессе эксплуатации дорог, связанных с гидравлическими явлениями, эти сведения в определенной степени позволят установить их воздействие на эксплуатацию автомобильной дороги.

В методических рекомендациях рассматриваются задачи по расчету равномерного движения воды в каналах. Как правило, ввиду возникновения тех или иных условий в сооружениях автомобильных дорог равномерное движение воды переходит в неравномерное и наоборот. Поэтому необходимо восстановить сведения предыдущей дисциплины «Гидравлика, гидрология, гидрометрия водотоков» по расчету каналов при равномерном движении воды. Неравномерное движение воды является достаточно сложным в сравнении с равномерным как в отношении расчетов, так и в понимании физической картины. В связи с этим рассматриваются основные характеристики открытых потоков, которые в той или иной степени отражают переход потока из бурного состояния в спокойное (удельная энергия, критическая глубина и критический уклон, параметр кинетичности – число Фруда).

Также в методических рекомендациях предлагаются задачи, которые позволяют определить или создать условия перехода потока из бурного со-

стояния в спокойное посредством гидравлического прыжка.

Одним из сложных практических вопросов является использование уравнения Бахметева для построения кривых свободной поверхности открытых потоков. Этому вопросу также посвящаются некоторые задачи.

Значительное количество задач в инженерной практике связано с проектированием водосливов (мосты, водопропускные трубы, водосбросные сооружения), в связи с чем излагается методика их решения.

Важным вопросом в гидравлике сооружений является проблема сопряжения бьефов, от которой зависит надежная работа водосбросного или водоотводного сооружения и эксплуатационное состояние дороги. В методических рекомендациях приводятся задачи по созданию благоприятного вида сопряжения бьефов путем устройства водобойных колодцев и водобойных стенок.

Водосбросным (быстротоки, перепады) и водопропускным (трубы) сооружениям также уделено немало внимания.

5

1 Равномерное движение воды в каналах

При равномерном движении воды в каналах наблюдается равновесие сил, вызывающих движение (проекция силы тяжести на направление движения), и сил сопротивления движению (сила трения воды о дно и стенки канала).

Различают три типа задач по гидравлическому расчету каналов. Первый тип. Определение величины расхода воды в канале Q. Все

остальные характеристики канала известны: уклон дна канала i, площадь живого сечения ω и его характеристики (коэффициент шероховатости – n, гидравлический радиус – R). Задача решается с помощью формулы Шези:

где ω – площадь живого сечения, м2, для трапецеидального канала находится по формуле

где b – ширина канала по дну, м;

h – глубина наполнения канала, м;

m – коэффициент заложения откосов, зависит от рода грунта или вида крепления дна и откоса канала. Выбирается согласно таблице 1.1;

С – коэффициент Шези, м0,5 /c , определяется по формуле Ман-

нинга

n – коэффициент шероховатости стенок и русла канала, выбирается согласно таблице 1.2.

Таблица 1.1 − Значение коэффициентов откоса в зависимости от рода грунта и укрепления канала

6

Таблица 1.2 − Коэффициент шероховатости поверхности каналов

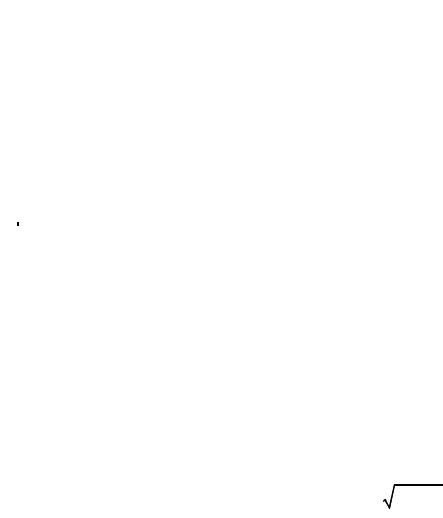
7

Окончание таблицы 1.2

Рассматриваемый тип задач при расчете сооружений практически не встречается. Величина расхода определяется на основании гидрологических расчетов.

Второй тип. Определяется уклон канала i. Все остальные данные известны. Задача решается на основании формулы Шези (1.1):

Такой тип задач встречается редко.

Третий тип. Необходимо определить размеры канала (ширину канала по дну – b или глубину наполнения – h), коэффициент заложения откосов m для каналов зависит от вида грунта (см. таблицу 1.1). При расчете

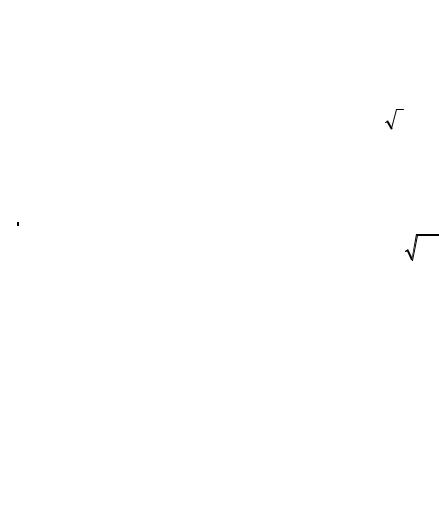
8

сооружений автомобильных дорог чаще всего приходится находить глубину потока на подходе к сооружению (глубину потока верхнего бьефа – hВБ) или после сооружения (глубину нижнего бьефа – hНБ).

В этом случае известными являются: Q, b, i, m, n (расход, ширина канала по дну, уклон дна канала, коэффициенты заложения откосов и шероховатости).

Решение задачи заключается в следующем.

По заданному расходу Q и величине уклона канала i определим необходимую расходную характеристику:

Решение задачи проводится графоаналитическим способом. Задаются рядом значений h (не менее трех – h1 , h 2 , h 3 ) и для каждого из них под-

считывают расходную характеристику Ki по формуле

Расчет значений расходной характеристики для различных h удобнее проводить в табличной форме (таблица 1.3).

Таблица 1.3 − Расчет глубины наполнения канала h

При h1 = 0 К1 = 0. Значения ω, χ, R, C и К вычисляются соответст-

венно по формулам (1.2)−(1.5), (1.8). Необходимо, чтобы Кн находился в диапазоне К1−К3. По данным таблицы строится график К = f(h) (рисунок 1.1). Ось h располагается вертикально.

Используя значение Кн из (1.7), по кривой К = f(h) находят глубину воды в канале hн, которая и будет глубиной подводящего к сооружению или отводящего от сооружения русла.

Задача. Уклон канала i = 1 ‰, ширина по дну в = 1,0 м, коэффициент заложения откосов m = 2,5. Определить наполнение канала, если необходимо пропустить расход Q = 1,4 м3/с.

9

Рисунок 1.1 – Определение глубины наполнения канала

2 Критическая глубина и критический уклон. Бурное и спокойное состояние потока

При критической глубине hк поток обладает минимальной энергией. Уклон дна русла, при котором устанавливается критическая глубина, называется критическим iк.

Минимум энергии потока определяется уравнением

где ωк− площадь живого сечения потока при критической глубине, м2; Bк − ширина потока по верху, м;

α − коэффициент Кориолиса, α = 1,0−1,1; Q − величина расхода, м3/с;

g − ускорение силы тяжести g = 9,8 м/с2.

Для потоков трапецеидального живого сечения критическую глубину обычно определяют графическим способом. Для этого, задаваясь рядом значений глубин h, находят ω, B , а затем − ω 3/В. Расчет удобнее производить в табличной форме. По результатам таблицы строим график

ω3/В = f(h) (рисунок 2.1).

На графике вдоль оси ω 3/В откладываем значение (α · Q2)/g и по кривой находим hк.

Для прямоугольного русла критическая глубина находится по формуле

10

Рисунок 2.1 − Определение критической глубины

По критической глубине потока определяется его состояние. Если глубина потока больше критической – спокойное состояние потока (h > hк); если меньше – бурное (h < hк). Это также можно определять по безразмерному критерию – числу Фруда

Физический смысл числа Фруда: отношение удельных энергий − кинетической к потенциальной. При критической глубине Fr = 1,0.

Для бурного потока (преобладает кинетическая энергия) Fr > 1,0, для спокойного (преобладает потенциальная энергия) – Fr < 1,0.

Задача 1. Определить бурное или спокойное состояние потока в канале прямоугольного сечения, если величина расхода Q = 12,0 м3/с, его ширина в = 4 м, а глубина наполнения h = 1,5 м.

Решение

Используя зависимость (2.2), определим критическую глубину:

Так как h = 1,5 м > hк = 1 м, поток находится в спокойном состоянии.

Задача 2. Определить расход воды в канале прямоугольного сечения шириной в = 4 м, если критическая глубина hк = 1,0 м.