
7452
.pdf
Она имеет единственное решение  то есть
то есть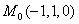 – единственная точка возможного экстремума функции при заданных условиях связи.
– единственная точка возможного экстремума функции при заданных условиях связи.
Вычислим второй дифференциал функции Лагранжа 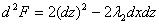 и подстав-
и подстав-
ляя 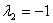 и
и 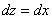 , найденное из первого уравнения связи, получаем положительно определенную квадратичную форму от переменной
, найденное из первого уравнения связи, получаем положительно определенную квадратичную форму от переменной  при
при 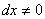 . Отсюда следует, что функция при заданных условиях связи имеет в точке
. Отсюда следует, что функция при заданных условиях связи имеет в точке 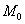 условный ми-
условный ми-
нимум.
Пример 3. (показывает, что в правиле множителей Лагранжа не всегда можно полагать 0 1).
32 fx,xxinf;fx,xxx0.
0121 11212
Решение. Функции f0 |
и f1 |
непрерывно дифференцируемы. Из условия |
|||||||
3 |
2 |
|
|
|
3 |
2 |
|
|
|
x x 0 следует, |
что x x 0 x 0. Поэтому очевидно, что решение задачи |
||||||||
1 |
2 |
|
|
|
1 |
2 |
1 |
|
|
x 0, 0 |
|
|
|
|
|
|
1 |
|
|
Если прямо следовать Лагранжу, то надо положить 0 |
|
, составить |
|||||||
|
. |
|
|||||||
|
|
|
|
|
3 2 |
|
|
|
|
сумму |
Lx x x |
|
далее решать систему |
|
уравнений |
||||
|
1 |
1 2 и |
|
||||||
L0 |
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
1 |
|
13x 0 |
|
|
|
|
|||
|
|
1 |
. Из последней системы следует, что 0 (так как в про- |
||||||
|
|
|
|||||||
|
|
|
|||||||
L0 |
2x0 |
|
|
|
|
||||
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
тивном случае не будет удовлетворяться первое уравнение системы), тогда решение
|
|
1 |
|
|
|
|
|
системы имеет вид: |
x |
, x0 |
x , x |
не будет удов- |
|||
1 |
3 |
2 |
. Но при этих значениях |
1 2 |
|||
|
|
|
|
||||
|
|
3 |
2 |
0. Таким образом, получим что решения нет, |
|||
летворяться уравнение связи x |
x |
||||||
|
|
1 |
2 |
|
|
|
|
а это неверно.
Пример 4. (показывает, что экстремум функции Лагранжа как задачи без огра-
ничений может не совпадать с экстремумом исходной задачи с ограничениями).
2 3 fx;xxxinf;fx;xxx0.
01221 11211
41

|
Решение. Очевидно, что решение задачи |
x 0, 0 |
(так как |
|
|
из |
условия |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
3 |
0 следует, |
|
что x |
0 , а решение задачи |
2 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
0 ). Функ- |
|||||||||||||||||||||||||
x x |
|
x |
inf имеет вид |
2 |
|||||||||||||||||||||||||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
ция Лагранжа записывается в виде: |
L xx xx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
02 |
1 1 1. Необходимое усло- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
L0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
13x 0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, то 0 и из первого |
||||||||||||||||||||
вие экстремума: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Если |
|
0 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
L 0 |
|
2x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 3x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||||
уравнения системы следует, |
что |
|
|
|
2 |
|
|
– противоречие. Значит, |
|
|
0 |
|
. Поло- |
||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|||
жим |
|
. Тогда функция Лагранжа примет вид: |
Lx x xx |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
2 1 |
1 1. Очевид- |
||||||||||||||||||||||||||||||||||||
но, |
что |
|
L0, 0 0 |
Пусть |
0 произвольное действительное |
число. Тогда |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
L,0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L, 0 0 |
|
|
|
|
|
L, 0 0 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
, при |
0 |
и |
|
|
|
|
при |
||||||||||||
|
1) Если 0 , то 10. Тогда |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Если 0 , то |
L, 0 |
|
|
|
L, 0 0 |
при 0 |
и |
L, 0 0 |
при |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L, 0 0 |
|
|
|
|
|
1 |
|
L, 0 0 |
|
|
||||||||||||||||||||
|
3) |
|
Если |
|
0 1, |
то |
|
при |
|
|
|
|
|
;0 |
|
при |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0; |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L, 0 0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
L, 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||
|
4) |
|
Если |
|
|
|
, то |
|
|
|
|
|
|
3 |
и, следовательно, |
|
|
|
|
|
|
|
при |
|
|
|
и |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
L, 0 0 |
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L, 0 0 |
|
|
|
|
|
|
|
||||
|
5) |
|
Если |
|
1, |
то |
|
|
|
|
2 |
|
|
|
|
|
следовательно, |
|
|
|
|
|
|
|
при |
|
0 и |
||||||||||||||||||
|
|
|
|
10и, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
L, 0 0 |
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Таким образом, при любых функция L принимает в любой достаточно малой |
||||||||||||||||||||||||||||||||||||||||||||
окрестности точки 0, |
0 |
|
как положительные значения, так и отрицательные значе- |
||||||||||||||||||||||||||||||||||||||||||
ния. А это означает, что ни при каких |
|
эта функция в точке |
x 0, 0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
не имеет да- |
||||||||||||||||||||||||||||||||||||||||||
42

же локального минимума. Значит, точка x 0, 0 не является решением задачи, а
это неверно.
Задача 5.
На развитие двух предприятий выделено 2 млн. рублей. Если первому предпри-
ятию дадут x1 млн. рублей, то прибыль, полученная от этого предприятия, будет
|
|
|
|
|
равна 2 x1 |
млн. рублей, если x2 млн. дадут второму, то прибыль от него будет равна |
|||
|
|
|
|
|
3 x2 млн. |
рублей. Определить, как следует распределить средства между предпри- |
|||
ятиями, чтобы суммарная прибыль была максимальной. Решим эту задачу методом множителей Лагранжа.
Задача |
состоит в отыскании точки глобального максимума функции |
|||
|
|
|
|
|
f 2 x1 + 3 |
x2 при ограничении x1 + x2 = 2 |
|||
Точку возможного максимума найдем методом множителей Лагранжа. Функ-
ция Лагранжа имеет вид:
L(x1, x2 , ) 2
 x1 3
x1 3
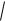 x2 (x1 x2 2)
x2 (x1 x2 2)
Для отыскания точек возможных экстремумов составим систему:
L |
|
1 |
|
|
0 |
|||||
|
|
|
|
|||||||
|
x1 |
|
|
x1 |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
3 |
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
x2 |
|
2 |
|
x2 |
|
|||||
|
|
|
|
|
||||||
L |
x x |
|
|
2 0 |
||||||
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
x |
||||||
|
Найдем ее решение. |
|
|
|
|
|
2 |
x |
|
|
3 |
x |
x |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
2 x2 |
|
|
|
|
|
2 |
|
|
|
1 |
|
2 |
|
4 1 |
|||||
|
Подставим |
|
найденное |
|
|
соотношение |
|
|
x |
|
|
9 |
x |
в |
|
уравнение (3), получим |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
1 |
|
|
|
|
|
|
x |
9 |
x 2 0 |
13 |
|
x |
2 x |
8 |
|
и тогда x |
|
|
18 |
. Находим : |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1 |
4 |
1 |
|
|
4 |
1 |
1 |
13 |
|
|
|
|
|
|
|
|
2 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Итак, система имеет одно решение
43

|
|
8 |
|
18 |
|
|
13 |
|||
P0 |
|
|
|
; |
|
|
; 0 |
|
|
|
13 |
13 |
8 |
|
|||||||
|
|
|
|
|
|
|||||
Исследуем найденную точку на локальный условный экстремум с помощью определителя L
y x1 , x2 x1 x2 2
y |
1; y |
1 |
x1 |
x2 |
|
L |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x1 |
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
L |
2 |
|
|
|
|
1 |
|
|
|
; L |
|
|
P |
|
|
13 |
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
0 |
|
|
|
|
|
|
|
32 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
L |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x2 |
|
2 |
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
L 2 |
|
|
|
|
|
|
3 |
|
|
|
; L |
|
|
P |
|
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
x2 |
|
|
|
4 |
|
|
|
|
x2 |
3 |
|
|
|
x2 |
|
|
0 |
|
|
|
|
|
|
|
72 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Подставив все в формулу получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
13 |
|
|
13 |
|
|
13 |
|
13 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
13 |
|
13 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
32 |
|
2 |
|
|
|
|
72 |
|
|
2 |
|
|
32 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
2 |
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Так как |
|
0 , то Po |
|
; |
|
|
|
|
|
|
|
|
– точка локального условного максимума. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Чтобы показать, что именно в точке |
Po достигается и глобальный максимум, |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
перейдём к задаче на отыскивание безусловного максимума функции одной пере- |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
менной. С помощью задачи x1 x2 |
|
2 , запишем условную функцию в виде: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
f (x1, x2 ) 2
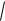 x1 3
x1 3
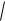 x2 2
x2 2
 x1 3
x1 3
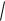 2 x1 y(x1)
2 x1 y(x1)
Требуется найти такую точку, где достигается наибольшее значение функции.
Область возможного изменения оставшейся переменной отрезок [0;2].
44
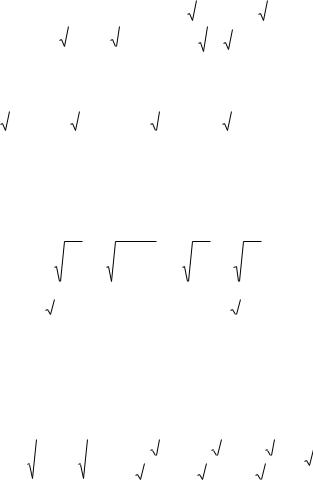
Непрерывная функция на замкнутом отрезке обязательно достигает своего наи-
большего значения либо в критических точках внутри отрезка, либо на концах от-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
резка: |
y (x1 ) |
1 |
|
|
|
|
3 |
|
|
2 2 x1 3 x1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x1 |
|
2 2 x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 x 2 x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из условия y (x1 ) 0 находим стационарную точку |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
(0;2) |
||||||||||||
2 |
|
2 x |
3 |
x |
|
|
0 2 |
|
2 x 3 |
x 4(2 x ) 9x |
8 4x |
9x |
13x |
8 x |
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
13 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Точек, где производная не существует, внутри отрезка нет. Находим значение
целевой функции в стационарной точке и на концах отрезка.
y( |
8 |
) 2 |
18 |
|
3 |
2 |
8 |
|
2 |
8 |
|
3 |
18 |
|
1,56 3,35 5,09 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
13 |
13 |
|
|
13 |
|
13 |
|
13 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
y(0) 3 |
2 4,24 |
|
|
|
|
y(2) 2 |
2 2,83 |
|||||||||||||
Мы видим, что наибольшее значение достигается в точке x |
|
8 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
13 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
И так, глобальный максимум достигается при x |
8 |
млн.руб., x |
|
|
|
18 |
млн.руб. |
||||||||||||||||||||||||||||
|
2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
13 |
|
|
|
13 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
8 |
|
|
18 |
|
|
2 2 |
2 |
|
3 3 |
2 |
|
13 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
y 2 |
|
3 |
|
|
|
|
|
26 5,09млн.руб. |
|
|
|
|
|
|
|
||||||||||||||||||||
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
13 |
13 |
13 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Пример 6.
Планируется деятельность четырех промышленных предприятий на год. На-
чальные средства 5 млрд усл. руб. Средства, вложенные в k-е предприятие, приносят в конце года доход fk(x). Эти функции заданы таблично:
x |
f1 |
f2 |
f3 |
f4 |
0 |
0 |
0 |
0 |
0 |
1 |
8 |
6 |
3 |
4 |
2 |
10 |
9 |
4 |
6 |
3 |
11 |
11 |
7 |
8 |
4 |
12 |
13 |
11 |
13 |
5 |
18 |
15 |
18 |
16 |
Считаем, что работа предприятия не влияет на работу других предприятий и суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.
Определить, какое количество средств нужно выделить каждому предприятию, что-
45
бы суммарная прибыль была наибольшей.
Решение
Итоговая таблица:
|
|
x |
|
Z1 |
Z2 |
|
Z3 |
|
|
|
Z4 |
x1 |
|
x2 |
|
|
|
x3 |
x4 |
|
|
|
|
0 |
|
0 |
0 |
|
0 |
|
|
0 |
0 |
|
0 |
|
|
0 |
0 |
|
|
||
|
|
1 |
|
8 |
8 |
|
8 |
|
|
8 |
1 |
|
0 |
|
|
0 |
0 |
|
|
||
|
|
2 |
|
10 |
14 |
|
14 |
|
|
14 |
2 |
|
1 |
|
|
0 |
0 |
|
|
||
|
|
3 |
|
11 |
17 |
|
17 |
|
|
18 |
3 |
|
2 |
|
|
0,1 |
1 |
|
|
||
|
|
4 |
|
12 |
19 |
|
20 |
|
|
21 |
4 |
|
2,3 |
|
|
1 |
1 |
|
|
||
|
|
5 |
|
18 |
21 |
|
22 |
|
|
24 |
5 |
|
3,4 |
|
|
1 |
1 |
|
|
||
|
Расчетная таблица: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Z2 |
x2 |
f2 |
Z1 |
f2+Z1 |
|
|
|
f3 |
Z2 |
f3+Z2 |
|
|
|
f4 |
Z3 |
f4+Z3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x=1 |
0 |
|
0 |
8 |
8 |
|
|
|
0 |
8 |
8 |
|
|
|
0 |
8 |
8 |
||||
|
|
1 |
|
6 |
0 |
6 |
|
|
|
3 |
0 |
3 |
|
|
|
4 |
0 |
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x=2 |
0 |
|
0 |
10 |
10 |
|
|
|
0 |
14 |
14 |
|
|
|
0 |
14 |
14 |
||||
|
|
1 |
|
6 |
8 |
14 |
|
|
|
3 |
8 |
11 |
|
|
|
4 |
8 |
12 |
|||
|
|
2 |
|
9 |
0 |
9 |
|
|
|
4 |
0 |
4 |
|
|
|
6 |
0 |
6 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x=3 |
0 |
|
0 |
11 |
11 |
|
|
|
0 |
17 |
17 |
|
|
|
0 |
17 |
17 |
||||
|
|
1 |
|
6 |
10 |
16 |
|
|
|
3 |
14 |
17 |
|
|
|
4 |
14 |
18 |
|||
|
|
2 |
|
9 |
8 |
17 |
|
|
|
4 |
8 |
12 |
|
|
|
6 |
8 |
14 |
|||
|
|
3 |
|
11 |
0 |
11 |
|
|
|
7 |
0 |
7 |
|
|
|
8 |
0 |
8 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x=4 |
0 |
|
0 |
12 |
12 |
|
|
|
0 |
19 |
19 |
|
|
|
0 |
20 |
20 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
6 |
11 |
17 |
|
|
|
3 |
17 |
20 |
|
|
|
4 |
17 |
21 |
|||
|
|
2 |
|
9 |
10 |
19 |
|
|
|
4 |
14 |
18 |
|
|
|
6 |
14 |
20 |
|||
|
|
3 |
|
11 |
8 |
19 |
|
|
|
7 |
8 |
15 |
|
|
|
8 |
8 |
16 |
|||
|
|
4 |
|
13 |
0 |
13 |
|
|
|
11 |
0 |
11 |
|
|
|
13 |
0 |
13 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x=5 |
0 |
0 |
18 |
|
|
18 |
|
0 |
21 |
|
|
21 |
|
0 |
22 |
22 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
6 |
12 |
|
|
18 |
|
3 |
19 |
|
|
22 |
|
4 |
20 |
24 |
||||
|
|
2 |
9 |
11 |
|
|
20 |
|
4 |
17 |
|
|
21 |
|
6 |
17 |
23 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
11 |
10 |
|
|
21 |
|
7 |
14 |
|
|
21 |
|
8 |
14 |
22 |
||||
|
|
4 |
13 |
8 |
|
|
21 |
|
11 |
8 |
|
|
19 |
|
13 |
8 |
21 |
||||
|
|
5 |
15 |
0 |
|
|
15 |
|
18 |
0 |
|
|
18 |
|
16 |
0 |
16 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Наибольшая прибыль 24 млрд усл. руб. может быть получена, если рас-
пределить средства между предприятиями следующим образом: (1,2,1,1).
Пример 7. Имеется определенное количество ресурсов S0=100, которое необходимо
46

распределить между n=4 хозяйствующими субъектами на текущую деятельность в течение рассматриваемого периода (месяц) с целью получения совокупной макси-
n
мальной прибыли. Размеры вложений ресурсов xi (i 1, n ; xi So ) в деятельность
i 1
каждого хозяйствующего субъекта кратны величине h=20 и заданы вектором Q. Из-
вестно, что каждый хозяйствующий субъект в зависимости от объема используемых средств xi за рассматриваемый период приносит прибыль в размере fi (xi ) ( i 1, n )
(не зависит от вложения ресурсов в другие хозяйствующие субъекты):
|
|
0 |
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
20 |
|
|
|
|
14 |
17 |
22 |
20 |
|
|
|
|
|
|
|
|
|||||
|
|
40 |
|
; |
|
|
26 |
20 |
21 |
33 |
|
Q |
|
|
|
f (x) |
|
|
|
|
|
|
|
60 |
|
|
35 32 |
37 |
46 |
||||||
|
|
80 |
|
|
|
|
52 |
61 |
67 |
30 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
61 |
72 |
58 |
42 |
|
|
100 |
|
|
|
|
|
|||||
Необходимо определить, какой объем ресурсов нужно выделить каждому пред-
приятию, чтобы суммарная прибыль была наибольшей.
Решение. Особенности модели: ограничения линейные, но переменные цело-
численные, а функции fi (xi ) заданы таблично, поэтому нельзя применить методы целочисленного программирования.
Составим рекуррентные уравнения Беллмана (обратную схему):
Zn* (Sn 1) |
|
|
max |
fn (xn ) , |
|
|
|
|
|
|
|
||
|
|
|
0 xn Sn 1 |
|
|
|
|
|
|
|
|||
Zk* (Sk 1) |
|
|
|
{ fk (xk ) Zk* 1(Sk )} |
|
|
|
|
|||||
|
|
max |
( k n 1,1) , |
(13) |
|||||||||
|
|
|
0 xk Sk 1 |
|
|
|
|
|
|
|
|||
Z |
max |
Z *(S |
0 |
) |
max { f (x ) Z *(S )} |
. |
|
|
|
||||
|
1 |
|
|
1 |
1 |
2 |
1 |
|
|
|
|||
|
|
|
|
|
0 x1 S0 |
|
|
|
|
|
|
|
|
Определим условные максимумы в соответствии с уравнениями (13), результа-
ты расчетов представлены в табл. 6.
По результатам условной оптимизации определим оптимальное распределение ресурсов:
47
S |
Z |
max |
Z * (S |
) x* S S |
x* Z * (S ) x* S |
n 1 |
S |
n 2 |
x* |
1 |
|
|
0 |
|
1 0 |
1 1 0 |
1 2 1 2 |
|
n |
|
|||||
Z * (S |
n 1 |
) x* . |
|
|
|
|
|
|
|
|
||
|
n |
|
n |
|
|
|
|
|
|
|
|
|
S0 100 Z max Z1* (S0 ) Z1* (100) 87 x1* 0
S1 S0 x1* 100 0 100 Z2* (S1 ) Z 2* (100) 87 x2*
S2 S1 x2* 100 0 100 Z3* (S2 ) Z3* (100) 87 x3*
S3 S2 x3* 100 80 20 Z 4* (S3 ) Z 4* (20) 22 x4*
S4 S3 x4* 20 20 0
0
80
20
Таким образом, оптимальное распределение ресурсов:
X * (x1* , x2* , x3* , x4* ) (0, 0, 80, 20) ,
которое обеспечит наибольшую прибыль в размере 87 усл. ден. ед.
Ответ: оптимальное распределение ресурсов: X * (0, 0, 80, 20) , которое обес-
печивает наибольшую прибыль в 87 усл. ден. ед.
48

Таблица 6. Расчет условных оптимумов
sk-1 xk |
sk |
k=3 |
k=2 |
k=1 |
|
|
|
f |
3 |
(x ) Z * (s ) |
Z |
* (s |
2 |
) |
x* (s |
2 |
) |
f |
2 |
(x |
2 |
) Z * (s |
2 |
) |
Z |
* (s ) |
x* (s ) |
f |
1 |
(x ) Z * (s ) |
Z |
* (s |
0 |
) |
x* (s |
0 |
) |
||||||
|
|
|
|
3 |
4 |
3 |
3 |
|
3 |
|
|
|
3 |
|
2 |
1 |
2 |
1 |
|
1 |
2 |
1 |
1 |
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
5 |
|
|
|
6 |
|
|
7 |
|
|
|
|
|
|
8 |
|
|
9 |
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
0 |
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
20 |
0 |
20 |
0+20=20 |
|
|
|
|
|
|
|
|
|
0+22=22 |
|
|
22 |
|
|
0 |
|
0+22=22 |
|
|
22 |
|
|
|
0 |
|
|
||||||||
|
|
|
|
|
|
22 |
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
20 |
0 |
22+0=22 |
|
|
|
|
|
|
|
17+0=17 |
|
|
|
|
|
|
|
14+0=14 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
40 |
0 |
40 |
0+33=33 |
|
|
|
|
|
|
|
|
|
0+42=42 |
|
|
42 |
|
|
0 |
|
0+42=42 |
|
|
42 |
|
|
|
0 |
|
|
||||||||
|
|
|
|
|
|
42 |
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
20 |
20 |
22+20=42 |
|
|
|
|
|
|
|
17+22=39 |
|
|
|
|
|
|
|
14+22=36 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
40 |
0 |
21+0=21 |
|
|
|
|
|
|
|
|
|
20+0=20 |
|
|
|
|
|
|
|
26+0=26 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
60 |
0 |
60 |
0+46=46 |
|
|
|
|
|
|
|
|
|
0+55=55 |
|
|
|
|
|
|
|
0+59=59 |
|
|
59 |
|
|
|
0 |
|
|
||||||||
|
|
|
|
|
|
55 |
|
|
|
20 |
|
|
|
|
|
59 |
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
20 |
40 |
22+33=55 |
|
|
|
|
|
|
|
17+42=59 |
|
|
|
|
|
14+42=56 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
40 |
20 |
21+20=41 |
|
|
|
|
|
|
|
|
|
20+22=42 |
|
|
|
|
|
|
|
26+22=48 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
60 |
0 |
37+0=37 |
|
|
|
|
|
|
|
|
|
32+0=32 |
|
|
|
|
|
|
|
35+0=35 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
80 |
0 |
80 |
0+30=30 |
|
|
|
|
|
|
|
|
|
0+68=68 |
|
|
|
|
|
|
|
0+72=72 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
68 |
|
|
|
20 |
|
|
|
|
|
72 |
|
|
20 |
|
|
|
|
73 |
|
|
|
20 |
|
|
||||||||
|
20 |
60 |
22+46=68 |
|
|
|
|
|
|
|
17+55=72 |
|
|
|
|
|
14+59=73 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
40 |
40 |
21+33=54 |
|
|
|
|
|
|
|
|
|
20+42=64 |
|
|
|
|
|
|
|
26+42=68 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
60 |
20 |
37+20=57 |
|
|
|
|
|
|
|
|
|
32+22=54 |
|
|
|
|
|
|
|
35+22=57 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
80 |
0 |
67+0=67 |
|
|
|
|
|
|
|
|
|
61+0=61 |
|
|
|
|
|
|
|
52+0=52 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
100 |
0 |
100 |
0+42=42 |
|
|
|
|
|
|
|
|
|
0+87=87 |
|
|
87 |
|
|
0 |
|
0+87=87 |
|
|
87 |
|
|
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
20 |
80 |
22+30=52 |
|
|
|
|
|
|
|
|
|
17+68=85 |
|
|
|
|
|
|
|
14+72=86 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
40 |
60 |
21+46=67 |
|
|
|
|
|
|
|
|
|
20+55=75 |
|
|
|
|
|
|
|
26+59=85 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
60 |
40 |
37+33=70 |
|
|
|
|
|
|
|
|
|
32+42=74 |
|
|
|
|
|
|
|
35+42=77 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
87 |
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
20 |
67+20=87 |
|
|
|
|
|
|
|
61+22=83 |
|
|
|
|
|
|
|
52+22=74 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
100 |
0 |
58+0=58 |
|
|
|
|
|
|
|
|
|
72+0=72 |
|
|
|
|
|
|
|
61+0=61 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 8. Решение задачи о загрузке
Контрольная работа содержит вопросы по N различным темам (в каждой теме
разное количество вопросов I). Каждый вопрос типа i имеет вес vi (i=1,2,…N), а также время, отводимое на ответ wi . Максимальное время, которое может затратить студент на контрольную работу, W. Требуется определить максимальное количество баллов (вес), которое может набрать студент за отведенное время W=30.
Данные приведены в таблице:
|
№ темы |
I |
wi |
|
vi |
|
|
1 |
≤5 |
2 |
|
2 |
|
|
2 |
≤6 |
4 |
|
3 |
|
|
3 |
≤4 |
1 |
|
2 |
|
|
4 |
≤3 |
4 |
|
4 |
|
|
5 |
≤5 |
7 |
|
6 |
|
|
6 |
≤6 |
5 |
|
5 |
|
|
7 |
≤5 |
3 |
|
4 |
|
|
8 |
≤7 |
2 |
|
2 |
|
|
Решить задачу, приведя ее к рекуррентным соотношениям. |
|||||
|
Сначала рассмотрим задачу в общей постановке. Если обозначить количество |
|||||
вопросов типа і через ki , то задача принимает следующий вид: |
||||||
max Z v1k1 v2k2 vnkn |
при ограничениях w1k1 w2k2 wnkn W , ki – |
|||||
неотрицательные числа.
Если отбросить требования целочисленности ki , то решение задачи нетрудно найти с помощью симплекс-метода. В самом деле, так как остается лишь одно ограничение, базисной будет только одна переменная, и задача сводится к выбору типа і,
для которого величина vi W  wi принимает максимальное значение. Исходная задача не является задачей линейного программирования, и для ее решения необходимо использовать метод динамического программирования. Следует отметить, что рассматриваемая задача может быть также решена с помощью методов целочисленного программирования.
wi принимает максимальное значение. Исходная задача не является задачей линейного программирования, и для ее решения необходимо использовать метод динамического программирования. Следует отметить, что рассматриваемая задача может быть также решена с помощью методов целочисленного программирования.
Каждый из трех основных элементов модели ДП определяется следующим образом.
