7286

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования

«Нижегородский государственный архитектурно-строительный университет»

Э.А. Кюберис

МОДЕЛИРОВАНИЕ СИСТЕМ ВОДОСНАБЖЕНИЯ И ВОДООТВЕДЕНИЯ

Учебно-методическое пособие

по дисциплине «Моделирование систем водоснабжения и водоотведения» для обучающихся по направлению подготовки 08.04.01 Строительства, направленность (профиль) Водоснабжение и водоотведение

Нижний Новгород

2022

МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования

«Нижегородский государственный архитектурно-строительный университет»

Э.А. Кюберис

МОДЕЛИРОВАНИЕ СИСТЕМ ВОДОСНАБЖЕНИЯ И ВОДООТВЕДЕНИЯ

Учебно-методическое пособие

по дисциплине «Моделирование систем водоснабжения и водоотведения» для обучающихся по направлению подготовки 08.04.01 Строительства, направленность (профиль) Водоснабжение и водоотведение

Нижний Новгород

ННГАСУ

2022

УДК 628

Кюберис Э.А. / Моделирование систем водоснабжения и водоотведения: учебнометодическое пособие по освоению дисциплины «Окислительные методы в технологиях очистки природных и сточных вод» / Э.А. Кюберис; Нижегородский государственный архитектурно-строительный университет.– НижнийНовгород: ННГАСУ, 2022. –29 с. – Текст : электронный.

Приведены указания по освоению дисциплины «Моделирование систем водоснабженияиводоотведения». Рассмотренысодержаниеипоследовательностьизложения материала, приведены примерные темы расчетно-графической работы, а также общие требования к содержанию и оформлению расчетно-графической работы.

Предназначено обучающимся в ННГАСУ для выполнения расчетно-графической работы по направлению подготовки 08.04.01 Строительство, направленность (профиль) Водоснабжение и водоотведение

© Э.А. Кюберис,

© ННГАСУ, 2022.

Содержание

1. Использование регрессионных моделей….……………………………….5 Список использованных источников…………………………………….....28

Использование регрессионных моделей

Планирование многофакторных экспериментов с количественной градацией изучаемых факторов. Полный и дробный факторный эксперименты, их характеристики. Проверка значимости коэффициентов регрессии и адекватности регрессии. Оптимизация многофакторных процессов. Использование регрессионных моделей в экстремальных экспериментах.

По характеру все модели объектов (процессов) могут быть подразделены на теоретические (аналитические) и эмпирические. Первые основаны на некоторых предположениях о механизмах процессов. Подобные модели были рассмотрены в разделе «Динамика биологических систем» учебного пособия по моделированию.

Но часто изучаемые объекты (процессы), например, в биологии и сельском хозяйстве, сложным образом зависят от нескольких взаимодействующих входных факторов и не имеют сколько-нибудь четкой теории о механизмах их функционирования. В этих случаях вынужденно используют эмпирические модели, где исследуемый объект представляется т.н. «черным ящиком», на который воздействуют факторы xi (внешние управляемые воздействия). Фиксируют выходные параметры (отклики объекта – yi) т.е. ответную реакцию на эти входные воздействия.

Каждый входной фактор xi может принимать определенное количество значений, называемых уровнями факторов. Множество возможных уровней фактора xi называется областью его определения. Эти области могут быть непрерывными и дискретными, ограниченными и неограниченными. Предполагается возможность управления факторами: либо поддерживать их на заданном уровне, либо изменять по программе. Т.е. предполагается возможность постановки активного эксперимента с объектом.

К исследуемым выходным параметрам (yi) также предъявляют ряд требований. Они должны быть:

-эффективными, то есть способствовать скорейшему достижению цели исследования;

-универсальными – быть характерными не только для исследуемого объекта, чтобы впоследствии можно было сопоставлять разные объекты и их модели;

- статистически однородными, то есть определенному набору значений входных факторов xi должно соответствовать определенное значение выходных параметров yi с точностью до погрешности эксперимента;

- легко вычисляться и иметь физический смысл; - существовать при любом состоянии объекта.

Мы ограничимся рассмотрениям моделей с одним выходным параметром (y). Геометрический аналог выходного параметра (функции отклика) называется поверхностью отклика.

Типичным примером подобных эмпирических моделей является полиномиальная регрессионная зависимость выходного параметра y от xi – набора входных факторов. Например, полином 2-й степени – квадратичная модель зависимости отклика y от двух входных параметров:

y=b0+b1x1+b2x2+b12 x1x2+b11 x12+b22 x22.

Подобные уравнения, по существу, являются первыми членами разложением в ряд Тейлора неизвестной функции отклика сложного объекта. Предполагается, что нескольких первых членов ряда Тейлора будет достаточно для адекватной аппроксимации этой неизвестной сложной зависимости y от xi. Если статистическая проверка подтвердит адекватность, то подобная эмпирическая зависимость станет дескриптивной моделью, пригодной для предсказания значений отклика y в тех условиях xi, где опыты не проводили, а также для проверки теоретических представлений (гипотез) о наборе входных переменных, степени их влияния на выходной параметр, характере их взаимодействия. Кроме того подобные эмпирические зависимости пригодны для решения оптимизационных задач, т.е. для поиска оптимальных значений xi, обеспечивающих максимум или минимум выходного параметра y.

Следовательно, при построении подобных эмпирических регрессий возникает комплекс задач: подбор по возможности простого полинома; планирование и реализация активного эксперимента, где в отдельных опытах задаются разные наборы значений xi и фиксируются отклики y; оценка по результатам эксперимента коэффициентов b регрессии; проверка адекватности полученной эмпирической модели и т.п. Именно эти задачи будут обсуждаться далее.

Множество точек факторного пространства {xi}, в которых проводится активный эксперимент, представляется с помощью плана эксперимента. Теория планирования эксперимента предложила подходы, позволяющие значительно увеличить точность эмпирических моделей при минимальном объеме опытов. Поясним некоторые подходы с помощью простого примера – задачи на взвешивании предметов А, В и С.

Традиционно экспериментатор стал бы взвешивать предметы по следующей схеме из четырех опытов. Вначале необходимо провести «холостое взвешивание» без предметов, чтобы определить нулевую точку весов, затем по очереди – каждый из предметов по отдельности.

Таблица 1.

Вес каждого предмета оценивается по результатам двух опытов, например, для предмета А:

А=y1-y0.

Известно, что кроме систематической ошибки весов, которую удается компенсировать с помощью результата «холостого взвешивания» (y0),

существует случайная ошибка любого взвешивания с дисперсией σ2(y). Поэтому дисперсия ошибки веса любого предмета, например,

А: σ2(А)=σ2(y1-y0)=2σ2(y).

Проведем теперь эксперимент для решения той же задачи, но по схеме, предлагаемой теорией планирования эксперимента.

Таблица 2.

Легко убедиться, что вес каждого объекта будет задаваться формулой

=(-С-y0 + А+y0 - В- y0 + А+В+С+y0)/2=(2А)/2

В= (- y'1- y'2+ y'3+ y'4)/2

С = (+ y'1- y'2- y'3+ y'4)/2

Найдем теперь дисперсию случайной ошибки оценки веса предмета А:

σ2(А)= σ2[(- y'1+ y'2- y'3+ y'4)/2]=4σ2(y)/4=σ2(y).

Аналогично дисперсии случайных ошибок оценок веса предметов В и С в два раза меньше, чем при традиционном эксперименте по взвешиванию,

хотя число опытов по прежнему четыре. Причина в том, что при традиционной схеме вес каждого предмета оценивался по двум опытам, в новом варианте схемы – уже по среднему значению четырех взвешиваний. В последнем случае оперируют всеми факторами (предметами взвешивания) так, чтобыкаждыйвес вычислялсяпорезультатамвсехчетырех опытов серии. Эту схему можно назвать многофакторной: здесь оперируют всеми входными факторами (тремя предметами) так, чтобы вес каждого предмета затем вычислялся по результатам («откликам» y') всех четырех опытов эксперимента.

Та же идея применима в значительно более сложных и трудоемких экспериментах. Например, выход некоторого ценного продукта (y) линейно зависитоттрехпеременных – внешнихфакторов,влияющихна моделируемый процесс биосинтеза: x1, x2, x3. Это могут быть температура, давление и концентрация субстрата. Необходимо по результатам эксперимента, состоящего из нескольких опытов, оценить с минимально возможной ошибкой коэффициенты b регрессии – линейной эмпирической модели:

y=b0+b1x1+b2x2+b3x3.

Если удастся подобрать оптимальный план эксперимента, то ошибки оценок выходной переменной (y) также будут минимально возможными.

Каждый входной фактор (переменную x) в эксперименте будем варьировать только на двух уровнях, условно обозначенных далее через «-1» и «+1» или просто «-» и «+». Так, если температура в наших опытах

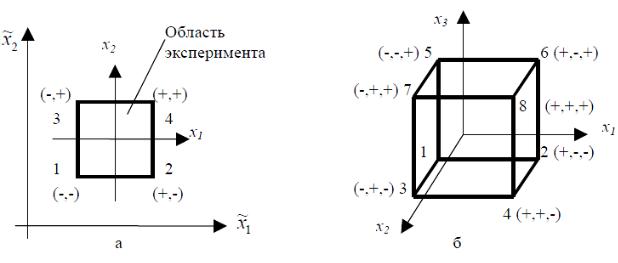
принимает два значения 1000 и 2000, то нижний уровень обозначим «-1», верхний – «+1». Геометрическойинтерпретацией подобногоподхода для двух входных факторовявляется квадрат в факторной плоскости (рис. а), для трех – куб (рис. б). Здесь нормированные координаты x1 и x2 проходят через точку пересечения средних уровней факторов, и масштаб их осей выбран так, чтобы интервал варьирования равнялся 1. Тогда условия проведения опытов будут соответствовать вершинами квадрата (куба), центром которого является средние уровни входных факторов.

Задание. На рисунке б укажите номера вершин куб, соответствующих плану эксперимента из табл. 2.

С целью перевода всех факторов в подобный масштаб делают преобразование начала координат факторов, т.е. переходят к нормированному (стандартному) масштабу

Таблица 3.

Задание. Объясните, сколько опытов в этом плане активного эксперимента следует провести, и на каких уровнях (верхнем или нижнем) в каждом опыте поддерживать входные факторы.

Здесь число опытов равно числу искомых коэффициентов регрессии (b0, b1, b2, b3). Подобные планы называются насыщенными.

Можно показать, что четыре коэффициента регрессии на основании четырех опытов, проведенных по схеме табл. 3, определяют по простым формулам:

с дисперсией случайной ошибки каждого коэффициента равной:

σ2(bi)=σ2(y)/4.

Здесь xij – нормированные значения входных факторов, т.е. «+1» или

«-1» из i–го столбца j–й строки-опыта плана из табл. 3, σ2(y) - дисперсия случайной ошибки измерения выходного параметра y в одном опыте.

Оценки bi конечно можно получить и по традиционной однофакторной схеме, где в каждом из четырех опыте только один из трех входных переменных фиксируется на верхнем уровне «+1», а остальные – на своих нижних уровнях «-1» (как в традиционной схеме взвешивания). Однако в этом случае дисперсия ошибки каждого коэффициента будет в два раза больше:

σ2(bi)=σ2(y)/2.

Продолжая эти рассуждения можно показать: чем больше входных факторов-переменных, тем больше выигрыш по точности экспериментальных оценок коэффициентов в эмпирической моделирегрессии. Например, если переменных семь (x1, x2,…, x7), то случайной дисперсия ошибки каждого из восьми коэффициентов: σ2(bi)=σ2(y)/(7+1). В

общем случае при n входных переменных σ2(bi)=σ2(y)/(n+1), если же использовать традиционную схему эксперимента, по-прежнему,

σ2(bi)=σ2(y)/2. Конечно, с увеличением числа переменных увеличивается и необходимое число опытов.

Линейной множественной регрессии далеко не всегда достаточно для адекватного описания изучаемого объекта (процесса). Аналогичный подход с успехом используется и при более сложной, нелинейной структуре эмпирических регрессионных моделей. В частности, разработаны соответствующие экспериментальные планы для т.н. регрессионных моделей первого порядка, где учитываются не только влияния основных факторов (xi), но также их возможные взаимодействия.

Например, в зависимости от взаимодействия температуры (x1) влияние давления (x2) на выходной параметр-отклик (y) может быть разным. Тогда регрессия с двумя входными переменными (x1, x2) с учетом их взаимодействия, выраженного через произведение x1×x2 , имеет вид:

y=b0+b1x1+b2x2+b12 x1×x2.

Соответствующий план эксперимента представлен в табл.4. Его структура полностью совпадает с планом табл. 3, но вместо b3 для третьей входной переменной x3 оцениваем b12 для взаимодействия двух факторов.

Для трех входных переменных и всех их взаимодействий регрессионная модель первого порядка выглядит следующим образом:

y=b0+b1x1+b2x2+b3x3+b12 x1×x2+b13 x1×x3+b23 x2×x3 +b123 x1×x2×x3.