
7281
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
А.С. Аистов, Н.Е. Демидова
ВЫПОЛНЕНИЕ КУРСОВОЙ РАБОТЫ ПО АНАЛИТИЧЕСКОЙ МЕХАНИКЕ
Учебно-методическое пособие по подготовке к лекционным и практическим занятиям по дисциплине
«Аналитическая механика» для обучающихся по направлению подготовки 08.03.01 Строительство
Профиль Промышленное и гражданское строительство
Нижний Новгород ННГАСУ
2016
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
А.С. Аистов, Н.Е. Демидова
ВЫПОЛНЕНИЕ КУРСОВОЙ РАБОТЫ ПО АНАЛИТИЧЕСКОЙ МЕХАНИКЕ
Учебно-методическое пособие по подготовке к лекционным и практическим занятиям по дисциплине
«Аналитическая механика» для обучающихся по направлению подготовки 08.03.01 Строительство
Профиль Промышленное и гражданское строительство
Нижний Новгород
2016
УДК 531/534(075)
Аистов А.С. Аналитическая механика [Электронный ресурс]: учеб.- метод. пос. / Н.Е. Демидова; Нижегор. гос. архитектур. - строит. ун - т – Н. Новгород: ННГАСУ, 2016. – 35с; 27 ил. 1 электрон. опт. диск (CD-R)
Пособие содержит примеры задач с решениями для выполнения расчётнографической(курсовой) работы по аналитической механике, а также варианты индивидуальных заданий.
Предназначено обучающимся в ННГАСУ для подготовки к лекционным практическим занятиям по направлению подготовки 08.03.01 Строительство
Профиль Промышленное и гражданское строительство.
© А.С. Аистов, Н.Е. Демидова
© ННГАСУ, 2016
3
Текст задач к вариантам заданий 1-30
Задача 1
Система тел А, В, Е, D, находящаяся в начальный момент времени в
состоянии покоя, начинает двигаться под действием сил тяжести. Определить время, за которое тело А пройдет путь равный S. Определить скорость и ускорение тела А в тот момент времени, когда оно пройдет путь S, учитывая трение скольжения тел. Считать, что качение тел происходит без проскальзывания. Нити считать нерастяжимыми и невесомыми. Решение выполнить, используя теорему об изменении кинетической энергии механической системы.
Задача 2
Определить реакции опор составной балки, используя принцип возможных перемещений.
Задача 3
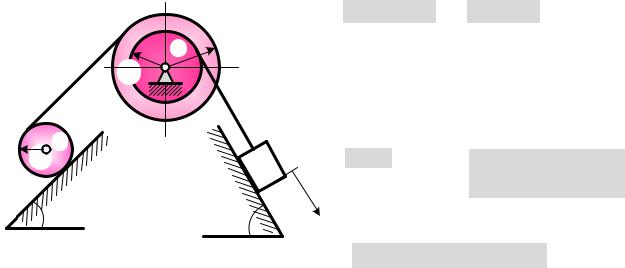
Механическая система движется под действием сил тяжести и пары сил с моментом М. Определить линейное (или угловое) ускорение согласно заданной на схеме (линейной или угловой) обобщенной координате. При решении задачи считать, что качение колес происходит без проскальзывания. Колеса считать однородными дисками, а нити – нерастяжимыми. Массы нитей и силы трения не учитывать. Решение выполнить с помощью уравнений Лагранжа II рода.
4
Пример решения варианта задач 1-3
Задача 1
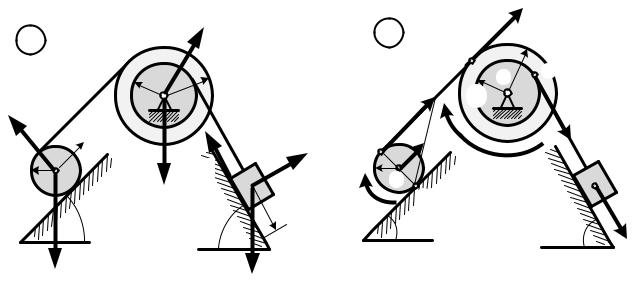
Система тел А, В, Е, D, находящаяся в начальный момент времени в
состоянии покоя, начинает двигаться под действием сил тяжести. Определить время, за которое телоАпройдет путь равный S. Определить скорость и ускорение телаА в тот момент времени, когда оно пройдет путь S, учитывая трение скольжения тел. Считать, что качение тел происходит без проскальзывания. Нити считать нерастяжимыми и невесомыми. Решение выполнить, используя теорему об изменении кинетической энергии механической системы.
|
|
|
|
Массы тел: |
|
B |
RB |
|
mA = 2m ; |
|
|
|
mB = m ; |
|
|
r B |
|
|
|
|
|
|
mС = m ; |
|
|
|
|
|
|
|
|
|
A |
m = 10 кг; |
C |
|
|
|
|
|
|
|
Углы: |
|
RC |
|
|
|
|
α |
|
β |
S |
α = 30°; |
|
β = 60°; |
|||
|
|
|||
|
|
|
|
vA , aA , t − ? |
Радиусы:
a = 10 см = 0.1 м;
RB = 4a = 40 см = 0.4 м; rB = 2a = 20 см = 0.2 м; RC = a = 10 см = 0.1 м;
Коэффициент
трения скольжения :
μ = 0.1;
при S = 2 м;
5
Решение
1. Изобразим на схеме механической системы (рис. а) все внешние силы:
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
vF |
|
|
|
|
а |
|
|
NB |
|
|
|
б |
|
RB |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
F |
|
|
||
|
|
|
RB |
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
B |
E |
|
|
R |
|
|
|
|
|
|
r B |
|
|
||
|
r B |
|
|
|
|
R |
|
R |
|||
|
|
|
|
|
|
|
vH |
|
|
||
NC |
|
|
|
|
|
|
|
|
v |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SC |
|
|
R |
|
H |
R |
|
|
|
|
|
|
|
N |
|
|
|
|
|
|||
|
|
|
A |
v |
|
|
|
|
|||
|
|
|
|
A |
RC |
C |
ωB |
|
|
A |
|
|
|
|
R |
|
|
|
|
||||
RC |
C |
|
FTP |
|
|
C |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
R |
|
|
ω |
|
|
|
|
|||
|
|
|
PB |
|
|
D |
|
|
|
R |
|
|
α |
|
|
SA = S |
C |
|
|
|
vA |
||
|
|
|
|
α |
|
|
β |
||||
|
|
β |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
R
PC R
PA
2.Обозначим буквами В и С точки в центрах колес В и С.
Обозначим буквой D точку касания колесаC с плоскостью.
Обозначим буквами E, F и H точки соприкосновения колес с нитями.
Выразим необходимые линейные и угловые скорости через искомую
скорость :
Тело A совершает поступательное движение со скоростью .
Нить нерастяжима, поэтому .
Клесо В совершает вращательное движение. Его угловая скорость направлена
по ходу часовой стрелки и равна |
|
|
|
|
|
|
|
. |
|
|
|||||||
|
|
|
|||||||||||||||
Скорость точки F равна |
|
|
|
|
∙ |
2 . |
|||||||||||
|
|
|
|||||||||||||||
Скорость точки Н равна |
2 . |
|
|
|
|
|
|
|
|
|
|
||||||
Колесо C совершает плоскопараллельное движение. МЦС находится в точке |
|||||||||||||||||
D. Угловая скорость направлена по ходу часовой стрелки и равна |
|||||||||||||||||
|
|
|
|
|
. |
||||||||||||
|
|
|
|||||||||||||||
Скорость точки С равна |
|
|
. |
|
|
||||||||||||
|
|
|
|||||||||||||||
3. Определим моменты инерции колес В и С.
|
|
6 |
|
|
|
|
|
|
|
|
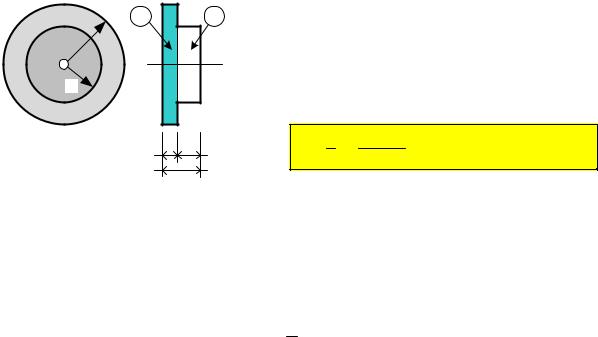
Колесо В имеет реборду. |
|
|
|
|||
|
|
Если |
толщина |
реборды |
составляет |
|||
R |
|
половину толщины колеса, момент инерции |
||||||
|
|
|||||||
|
Z |
колеса |
определяется |
по |
следующей |
|||
r |
|
формуле: |
|
|
|
|
|
|
δ1 |
δ2 |
JZ |
1 |
R4 + r4 |
|
|
|
δ1 = δ2 . |
|
δ |
= 2 m × |
R2 + r2 |
ï ðè |
óñëî âèè |
,÷ò î |
||
|
Поэтому |
|
|
|
|
|
|
|
J B |
= |
1 |
m × |
RB 4 + rB 4 |
= |
1 |
m × |
(4a)4 + (2a)4 |
=10ma2 . |
|
|
|
(4a)2 + (2a)2 |
||||||
ZB |
2 |
B RB 2 + rB 2 |
2 |
|
|
||||
Колесо С сплошное:
JZCC = 1 mC RC2 = 0.5ma2 .
2
4.Определим кинетическую энергию системы в начальном и конечном состояниях.
В начальном состоянии тело находится в состоянии покоя: |
0. |
|
||||||||||
В конечном состоянии кинетическая энергия равна |
, |
где |
||||||||||
Тело A: |
. |
|
|
$ 1.25 . |
|
|
|
|
|
|||
Тело B: |
|
! " |
# |
|
|
|
|
|
|
|||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
$ 0.75 . |
||||
Тело C: |
|
! " # |
|
|||||||||
|
||||||||||||
Сумма: |
1.25 0.75 3 . |
|||||||||||
5. Определим сумму работ всех внешних сил на заданном перемещении: |
|
|||||||||||
, |
/0 |
/0 |
0 |
/0 |
/0 |
|
|
/0 |
/0 |
1 |
||
) *+ *-. |
1 *-2 1 *-3ТР1 |
*-. 1 *-2 1 *-. 1 |
*-2 |
|||||||||
Учтем, что перемещения точек пропорциональны их скоростям, и |
||||||||||||
поскольку то и6 6 6. |
|
|
|
|
|
|
|
|
|
|||
Точка B неподвижна, поэтому |
*-. 1 0, *-2 1 0. |
|
|
|
|
|
||||||
/0 |
/0 |
|
|
|
|
|
|
|||||
2 |
2 |
направлены перпендикулярно к направлению |
|
|
||||||||
Реакции /0 |
и /0 |
|
|
|||||||||

|
|
|
7 |
0, *-2 1 0. |
|
|
|
движения, |
поэтому |
*-2 1 |
|
|
|||
/0 |
|
/0 |
|
|
|||
/0 |
9 6 |
∙ sin = 2 9 6 ∙ 0.68 1.72 9 6 |
. |
|
|||
*-. 1 |
|
|
|||||
0 |
|
@3ТР6 @A 2 6 @A 9 ∙ cos = ∙ 6 @0.1 9 6 |
. |
||||
*-3ТР1 |
|
||||||
/0 |
@ 9 6 ∙ sin D @0.5 9 6 |
. |
|
|
|||
*-. 1 |
|
|
|
||||
∑ *,+ *-./0 1 *-30ТР1 *-./0 1 1.72 96 @ 0.1 96 @ 0.5 96 1.12 96.
6.Найдем значение скорости тела А.
Используем теорему об изменении кинетической энергии механической системы:
|
@ ∑ *,+ . |
|
Так как 0, то |
∑ *,+ . |
|
Составим уравнение: |
3 1.12 9 6, |
(*) |
решая которое, получим, что F . IG H 2.71 мс .
7. Найдем ускорение тела А, продифференцировав равенство (*) по времени:
|
|
|
|
|
|
L. |
|
|
|
|
|
|
|
6 L 1.12 96 |
|
|
|
|
|
||||
|
6 |
|
|
6 L 1.12 9 |
|
|
|
|
|||
Учитывая, что |
L получим: |
|
|
|
|
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
м |
|
|
" L F |
. G |
F |
. G |
F |
.∙N.O |
1.35 |
. |
||||
M |
M |
M |
с |
||||||||
|
|
|
|
|
|
|
|
|
|
P |
|
8.Найдем время, за которое тело А пройдет путь, равный 2 м.
Запишем уравнение прямолинейного равноускоренного движения тела A:
|
6 " |
QP |
6 " |
QP |
, так как 0 и 6 0. |
|
|
|
|||
Отсюда |
R26⁄" R2 ∙ 2⁄1.35 1.72 T. |
||||
Ответ: 2.71 мс ; " 1.35 смP ; 1.72 T.
Задача 2
8
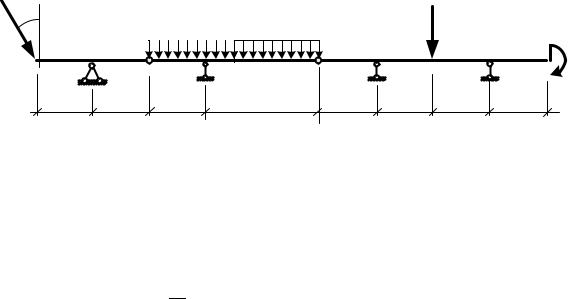
Определить реакции опор составной балки, используя принцип возможных
перемещений.
Дано:3 20 кН; . 40кН; Y 25 кНм; Z 10 кН; " 1м; D 30°.
2F
α |
|
q |
|
|
|
P |
М |
|
|
E |
|
H |
|
|
|
A |
|
B |
|
|
C |
|
D |
a |
a |
a |
2a |
a |
a |
a |
a |
Решение
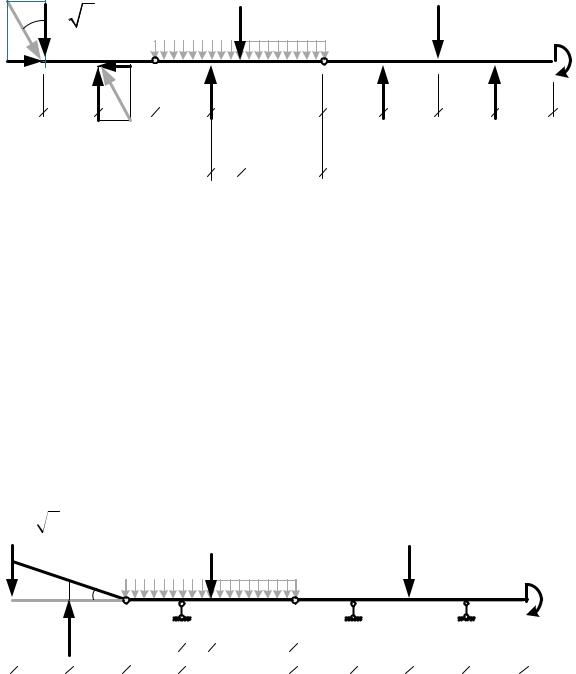
1.Разложим наклонную силу 2F на вертикальную и горизонтальную составляющие, модули которых равны:
23 T\]D 23 √I 3√3и 23]_`D 23 F.
Заменим распределенную нагрузку ее равнодействующей a 3Z"
30 кН.
Удалим связи, заменив их неизвестными реакциями, учитывая, что на неподвижной опоре реакция пройдет наклонно и может быть
представлена своими составляющими: вертикальной b и горизонтальной c .
Горизонтальная составляющая может быть найдена их уравнения
равновесия:
∑ c+ 0; 23]_`D @ c 0; откуда c 23]_`D 3.
Горизонтальная сила F и горизонтальная реакция c не совершают работу на вертикальных перемещениях, не влияют на величину вертикальных реакций и в последующих выкладках учитываться не будут.
|
|
|
9 |
|
|
F |
3 |
|
Q = 3qa |
P |
М |
|
|
||||
α |
|
E |
|
H |
|
|
A |
B |
|
C |
D |
F |
|
X A |
|
|
|
a |
a |
a |
2a |
a |
a |
a |
a |
|
|
|
|
|
|
|
|
Y |
R |
A |
R |
|
|
R |
RD |
|
|
||||||||
A |
|
B |
|
|
C |
|
||
|
|
|
|
0.5a |
|
1.5a |
|
|
|
|
|
|
|
b , и изобразим на |
|||
|
|
|
|
|
|
|
|
|
2. Удалим опору A, заменив ее неизвестной реакцией |
||||||||
рисунке виртуальные перемещения элементов системы.
Сумма работ внешних сил на этих перемещениях равна нулю в соответствии с принципом возможных перемещений. Составим
соответствующее уравнение:
b " de @ 3√3 ∙ 2" de 0, откуда
b @ 23√3 0, b 23√3 2 ∙ 20 ∙ 1.732 69.28 кН.
F 
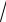 3
3
′ |
|
Q |
|
P |
A |
δϕ1 |
|
||
|
|
H |
М |
|
|
|
|
||
|
|
|
|
|
A |
E |
B |
C |
D |
|
|
YA |
|
|
0.5a |
1.5a |
|
|
a |
|
|
|
a |
a |
a |
|
2a |
a |
a |
a |
|
||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Удалим опору B, заменив ее неизвестной реакцией , и изобразим на рисунке виртуальные перемещения элементов системы.
