7148

ун-т. Междунар. ин-т экономики, права и менеджмента, Н.Новгород :

ННГАСУ, 1999.

4.4 Задания для самостоятельной работы

Раздел 1: Задачи линейной оптимизации.

Задача 1 Предприятие выпускает 2 вида продукции, используя 3 вида ресурсов. Принятые обозначения: А – матрица норм затрат сырья, В – запасы ресурсов, С – прибыль на единицу продукции:

Требуется:

1)Составить экономико-математическую модель задачи;

2)Определить план выпуска изделий (геометрическим способом и в

Excel), обеспечивающий получение максимальной прибыли;

3) Составить двойственную задачу, найти оптимальное решение и опти-

мум двойственной задачи с помощью теорем двойственности; указать де-

фицитные для предприятия ресурсы;

4)Определить интервалы устойчивости двойственных оценок ресурсов;

5)Проанализировать, как изменится максимальная прибыль предприятия в результате изменение запаса 1-го ресурса на 5 единиц;

6) Сколько решений имеет данная ЗЛП?

21

Задача 2 В упрощенной версии компания Oak Products производит только

2 вида стульев, Captain и Mate (вместо шести в полной версии). Составив экономический прогноз на следующую неделю, дирекция полагает, что можно будет продать все стулья марок Captain и Mate, которые компания в состоянии произвести. Требуется рекомендовать стратегию производства на следующую неделю, т. е. определить сколько стульев каждой марки нужно произвести, если руководство компании стремится максимизиро-

вать недельную валовую прибыль. При принятии решения в данной моде-

ли необходимо учитывать следующие факторы.

1)Стулья, произведенные компанией, продаются на той же неделе,

удельная валовая прибыль (доход минус расход) составляет 56$ для каж-

дого проданного стула марки Captain и 40$ для каждого стула марки Mate.

2) Для сборки стула нужны длинные штифты, короткие штифты и одно из двух типов сидений, которые имеются на складе в ограниченном количе-

стве. Запас длинных и коротких штифтов, которые можно будет использо-

вать на следующей неделе, составляет 1280 и 1600 шт. соответственно. Для производства одного стула марки Captain требуется 8 длинных и 4 корот-

ких штифта, а для производства стула Mate – 4 длинных и 12 коротких штифтов.

3)Запас ножек на следующую неделю составляет 760 штук.

4)Запас прочных и облегченных сидений составляет 140 и 120 штук, со-

ответственно. Для производства стульев Captain используют прочные си-

денья, а для Mate – облегченные.

5)Согласно договору между руководством компании и профсоюзом, общее

число произведенных стульев не может быть менее 100.

Задача 3. Три нефтеперегонных завода с ежедневной производительно-

стью 6, 5 и 6 млн. галлонов бензина снабжают 3 бензохранилища, еже-

22

дневная потребность которых составляет 4, 8 и 7 млн. галлонов соответ-

ственно. Бензин транспортируется в бензохранилища по бензопроводу.

Стоимость транспортировки составляет 10 центов за 1000 галлонов на од-

ну милю длины трубопровода. Потребности второго бензохранилища должны выполняться в обязательном порядке. В таблице приведены рас-

стояния (в милях) между

заводами и хранилищами. Отметим, что первый нефтеперегонный завод не связан трубопроводом с третьим бензохранилищем.

Найти оптимальную схему поставок бензина.

Задача 4 (Задача о доставке) Фирма обслуживает 5 клиентов. Каждый день она доставляет им товары на грузовых машинах. Существует 3 допусти-

мых маршрута доставки, каждый из которых позволяет обслужить опреде-

ленное количество клиентов и требует использования в течение дня одного транспортного средства. Каждый маршрут характеризуется определенны-

ми расходами (см. таблицу).

Необходимо выбрать такое множество маршрутов, при котором обеспечи-

вается обслуживание каждого клиента и, кроме того, суммарные расходы минимальны, при условии, что каждый клиент обслуживается один раз в день.

Задача 5

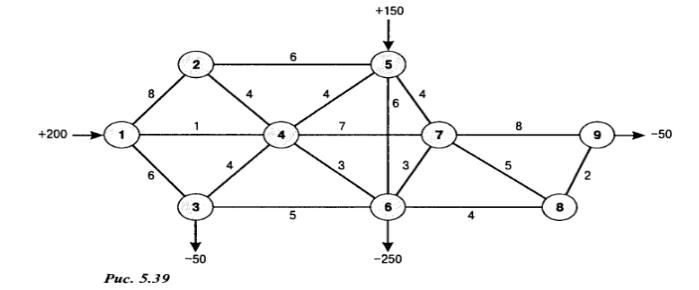
Дана сеть, показанная на рисунке 5.39. Узлы 1 и 5 ̶ это заводы, которые производят 200 и 150 грузовиков товара соответственно. Узлы 3, 6 и 9 ̶

это торговые точки, спрос в которых составляет 50, 250 и 50 грузовиков товара соответственно. Число рядом с дугой (i, j) показывает затраты на транспортировку одного грузовика товара из узла i в узел j. Решите задачу перевозки грузов. Чему равны суммарные затраты?

24

Раздел 2: Эконометрические модели.

Задача 1. Для зависимости Y от X, заданной корреляционной таблицей

где X,Y – прибыли (%) двух компаний.

1)оценить по МНК коэффициенты линейной регрессии Y = + X + U;

2)дать экономическое толкование построенной регрессии;

3)оценить значимость коэффициентов и ;

4)сделать точечный и интервальный прогноз при какомлибо X = x 0 ;

Задача 2. Имеются данные о разрешениях на строительство нового частно-

го жилья, выданных в США в 1990-1194 г.г., % к уровню 1987 г.

а) Определить сезонную компоненту и ее интенсивность, построить адди-

тивную модель с

25

учетом сезонной компоненты;

б) сделайте интервальный прогноз на декабрь 1994 г. и сравните его с фак-

тическим значением.

Пригодна ли модель для прогнозов?

Задача 3. В следующей таблице приведены данные по реальному ВНП

(GNP), реальному объему потребления (CONG) и объему инвестиций

(INV) для некоторой страны.

б) Оцените качество построенного уравнения, дайте экономическую ин-

терпретацию.

Задача 4. Пусть имеются данные об объемах потребления электроэнергии жителями региона за 16 кварталов:

26

Определить сезонную компоненту и ее интенсивность, построить аддитив-

ную модель с учетом сезонной компоненты. На рисунке показать аддитив-

ные показатели (Tt St ); выровненные уровни (Yt St ); линейный тренд Tt

27

О.В. Любимцев

Математические методы и модели в экономике

Учебно-методическое пособие

по подготовке к лекциям, практическим занятиям (включая рекомендации по организации самостоятельной работы) для обучающихся по дисциплине «Математические методы и модели в экономике» по направлению подготовки 38.03.02 Менеджмент профиль (Заочное) Производственный менеджмент

Федеральное государственное бюджетное образовательное учреждение высшего образования «Нижегородский государственный архи-

тектурно-строительный университет» 603950, Нижний Новгород, ул. Ильинская, 65.

http://www. nngasu.ru, srec@nngasu.ru

28