
6915
.pdf11
θ(x, y) =1 - Bi1 × y + 1 |
|
+ ∑ An |
×ϕn (y) × e-εn ×x |
. (1.35) |
||||
|
|
|
|
|
¥ |
|
|
|
1 + Bi1 |
+ |
Bi1 |
|
n=1 Bi1 |
|
|
||
Bi2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Анализ температурного поля (1.35) показывает, что при малых значениях безразмерной продольной координаты х от х=0 до х=х1 распределение температуры и скорости ее изменения по х в отдельных точках стены зависит от особенностей граничных условий при х=0. Математически в этой области поле температуры в стене будет определяться не только первым, но и последующими членами ряда (1.35). Эту область стены, непосредственно примыкающую к оконному проему, в которой скорость изменения температуры в направлении координаты х зависит от вида граничных условий при х=0, назовем по аналогии нестационарными температурными полями неупорядоченной областью теплопередачи через стену.
Начиная с некоторого расстояния х>х1 от оконного проема, граничные условия при х=0 начинают играть второстепенную роль, и процесс теплопередачи через стену полностью определяется только граничными условиями при у=0 и у=1, физическими свойствами материала стены и ее размерами и формой, хотя температурное поле вдоль стены и изменяется. Температурное поле в этой области х>х1 математически описывается первым членом ряда (1.35)
θ(x, y) = |
Bi1 × y + 1 |
|
+ |
A1 |
×ϕ1 (y) × e-ε1 ×x . |
(1.36) |
||
|
|
Bi1 |
|
|
||||
|
1 + Bi1 |
+ |
|
|
Bi1 |
|
||
|
Bi2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Безразмерный поток тепла, подводимый к стене на этом участке в предположении одномерного температурного поля, равен
|
|
|
|
Qo = - |
|
Bi1 × x 2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Bi |
. |
|
|
|
|
(1.37) |
|||||
|
|
|
|
|
1 + Bi1 |
+ |
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Bi2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Их отношение соответственно равно |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(1 + Bi1 |
+ Bi1 ) × ∑ An |
/ |
(0) × (1 - e |
-εn |
×x |
) - εn |
× ∫ϕn (y) × dy] |
|||||||||
|
|
×[ϕ n |
||||||||||||||||
|
|
|
¥ |
|
|
|
|
|
|
|
2 |
|
2 |
y1 |
|
|
||
Qд =1 + |
|
|
|
εn |
|
|
|
|
|
|
|
0 |
. |
|||||
|
Bi2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
n =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Qo |
|
|
|
|
Bi12 × x 2 |
|
|
|
|
|
|
|||||||
(1.38)
Как всякая теоретическая модель, аналитическая модель, приведенная выше, отражает главные особенности рассматриваемого явления и учитывает факторы, которые в соответствии с современными представлениями являются определяющими. Некоторые стороны процесса полагаются второстепенными и могут не учитываться. Только
12
экспериментальная проверка в достаточно полной мере позволяет оценить соответствие принятой аналитической модели реальным процессам.
1.2. Решения задач на вдув. Уравнение Фурье
Задачи на вдув широко распространены в авиационной и ракетной технике, поскольку часто возникает необходимость защитить стенки конструкции от воздействия высокотемпературного газового потока.
Такая техника защищается от перегрева жаростойкими, оплавляющимися или сублимирующими покрытиями или посредством конвективного, пористого, пленочного и заградительного охлаждения.
Но поскольку мы имеем дело с описанием движения воздушного потока вдоль внутренней поверхности наружного ограждения, нам необходимо рассмотреть лишь те варианты, из вышеперечисленных, которые могут удовлетворять заданным условиям. Таким образом, из рассмотрения выпадают различные типы теплоизолирующих покрытий.
Однако внимания заслуживает пористая система охлаждения, представляющую собой омываемую горячим газом стенку, выполненную из пористого материала, через которую в направлении горячего газа продавливается охладитель газ или жидкость. При прохождении через поры, охладитель получает теплоту от стенки, а выйдя на поверхность, ухудшает интенсивность теплообмена между горячим газом и стенкой. С одной стороны условия перехода теплоты от горячего газа к поверхности стенки ухудшаются, с другой стороны получаемая стенкой теплота выносится обратно в поток. Это приводит к снижению температуры стенки. При рассмотрении данной задачи применительно к православным храмам, стенкой является внутренняя поверхность оконного проема, горячим газом - восходящий конвективный поток, а вдуваемый газ или жидкость – холодный наружный воздух, проникающий в помещение храма через оконный проем.
Поскольку в космонавтике речь идет о высоких температурах, имеет место различие между поведением газовой фазы (эффузионное охлаждение) и жидкой фазы (конденсатное охлаждение). Эффузионное охлаждение является наиболее подходящим для заданных условий, поэтому в дальнейшем будет рассмотрено лишь газовое охлаждение через пористую стенку. Однако высокоскоростное движение газового потока и радиацион- но-конвективный теплообмен также не подходят под заданные условия.
Наиболее оптимально по отношению к заданным в исследовании условиям будет решение задачи, по условиям которой, интенсивность внутри пор бесконечно велика, и потому температурные поля стенки и протекающего по ней охладителя совпадают, а подходящий к холодной поверхности конвективный поток охладителя получает теплоту только путем теплопроводности.
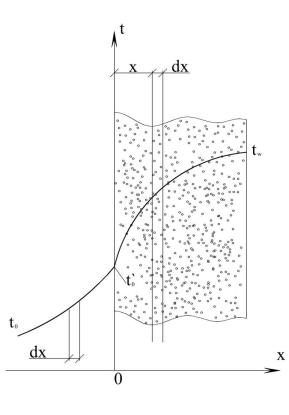
13
В сечении пористой стенки, отстоящем от начала координат на расстоянии x температура стенки и охладителя t (рис.1.3), а плотность тепло-
вого потока равна: |
qx |
= −λ |
dt |
|
(1.39) |
|
dx , |
||||||
|
|
|
|
|||
где λ - коэффициент теплопроводности пористого материала.
Рис. 1.3 Графическая иллюстрация к выводу формул при альтернативном решении задач на вдув (пористое охлаждение).
Значение температуры в сечении x+dx можно найти разложением t в ряд Тейлора. Ограничиваясь двумя членами выражение примет следующий вид.
tx+dx |
= t + |
dt |
dx |
(1.40) |
|
||||
|
|
dx |
|
|
Следовательно подставляя (2.48) в (2.49):
qx+dx |
= −λ |
d |
(t + |
dt |
dx) = −λ( |
dt |
+ |
d 2t |
dx) |
dx |
dx |
|
2 |
||||||
|
|
|
|
dx dx |
|||||
Разность тепловых потоков в сечениях x и x+dx расходуется на повышение энтальпии охладителя
− λ |
dt |
+ λ( |
dt |
+ |
d 2t |
dx) = g |
0*c p0 dt |
(1.41) |
dx |
|
|
||||||
|
|
dx dx2 |
|
|
||||
g0* - плотность массового потока охладителя, необходимая для обеспечения выбранной температур стенки, c p 0 - теплоемкость охладителя.
Уравнение (2.50) приводится к виду:

14
|
|
|
|
|
d 2t |
|
− |
g |
0*c p0 |
|
|
dt |
= 0 |
|
(1.42) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
dx2 |
|
|
λ |
|
|
dx |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Произведем замену ξ = |
g *c |
p 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
и получим следующие решения уравнения: |
|||||||||||||||||||
|
λ |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
t = Ñ |
1 + Ñ 2 eξx |
(1.43) |
||||||||||
Условия на границах стенки при x = 0;t = t`ω ; при x = δ ;t = tω |
позволяют |
||||||||||||||||||||
определить константы интегрирования |
|
|
|
|
|
|
|
|
|
||||||||||||
Ñ |
1 |
= t` − |
t`ω −tω |
; Ñ |
2 |
= |
t`ω −tω |
; |
|
||||||||||||
|
|
|
|
||||||||||||||||||
|
|
ω |
1 |
− eξδ |
|
|
|
|
|
1− eξδ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Подставляя константы интегрирования в уравнение (2.51) мы получим: |
|||||||||||||||||||||
|
|
t = t` + |
tω − t`ω |
|
(eξδ −1) |
(1.44) |
|||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
ω |
|
|
(eξδ |
−1) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
При рассмотрении баланса теплоты для слоя охладителя толщиной dx при x<0 позволяет записать дифференциальное уравнение для температуры охладителя
d 2t` − ζ |
dt` = 0 |
(1.45) |
dx2 |
dx |
|
g *c
Однако в данном уравнении ζ = 0 p 0 ,
λ0
где λ0 - коэффициент теплопроводности охладителя.
Решение этого уравнения имеет вид:
t`= C3 + C4 eζx
Граничные условия формулируются следующим образом:
При x = 0; λ0 dt` = λ dt ; при x = −∞;t`= t0 dx dx
Они позволяют найти константы интегрирования
C3 = t0 ; Ñ 4 |
= |
tω − t`ω |
|
eξδ − 1 |
|||
|
|
Подстановка констант в уравнение (1.45)
t`= t0 |
+ |
tω − t`ω |
eζx |
(1.46) |
|
||||
|
|
eξδ −1 |
|
|
При x = 0; t`= t`ω с помощью этого условия из уравнения (1.46) получается
t` = t |
0 |
+ |
tω − t0 |
|
|||
ω |
|
eξδ |
|
|
|
|
Это выражение позволяет исключить из (1.44) и получить окончательное выражение для температурного поля
t − t0 |
= e−ξδ (1− |
x |
) |
|
|
δ |
(1.47) |
||||
|
|||||
tω − t0 |
|
||||
15
Таким же образом можно провести параллели между конструкциями православных храмов и другими системами охлаждения.
При пленочном охлаждении защищаемая стенка покрывается пленкой жидкости, которая подается через одну или несколько щелей выполненных на некотором расстоянии друг от друга и растекается по поверхности. В храмах между окнами и оконными проемами также имеются неплотности, щели и зазоры, через которые холодный наружный воздух поступает в помещения храма. Однако при пленочном заграждении речь идет о совершенно других диапазонах скоростей, и выделяется так называемая критическая скорость, после достижения которой струя отделяется от охлаждаемой поверхности и может вернуться к ней на некотором расстоянии за щелью или совсем не попадает на нее. Также полностью исключается возможность образования волн на поверхности пленки, приводящих к потере устойчивости пленки, характеризующейся уносом капель неиспаренной жидкости газовым потоком.
Таким образом, при условиях, созданных в православных храмах интересным будет лишь уравнение теплового баланса при устойчивом движении пленки:
|
α |
(I r - Iω ) × l × h = G0 × Di0 |
(1.48) |
|
|
||
|
cρω |
, |
|
где: h – ширина пленки, l – длина пленки, G0 – |
массовый расход охлади- |
||
теля через щель, Di0 = cDt + r – изменение энтальпии охладителя в системе.
Варианты с загородительным и комбинированным (стенка омывается охлаждающим газом с двух сторон) охлаждением не могут быть использованы для православных храмов, поскольку поток охлаждающего газа поступает не со стороны стенки, а из плоскости перпендикулярной ей, чаще всего по касательной к тепловому потоку нагретой стенки или под углом 15-30º.
1.3. Численное моделирование теплообменных процессов
Приведённые выше основные уравнения были решены численно с помощью конечно-разностных методов. В процессе вычислений изменялся размер шага X, Y.
В обычном анализе свободной конвекции общие уравнения сводятся к так называемым уравнениям пограничного слоя путём оценки порядка величины членов исходных уравнений. Однако для рассматриваемой задачи ламинарного свободноконвективного следа такие упрощения не приемлемы из-за больших значений величин кромки пластины. В этом случае необходимо решать следующие уравнения:
|
¶Vx |
ρ × Vx |
|
|
¶x |
|
|
|
|
¶V |
x + |
|
¶Vy |
= 0 |
, |
|
|
|
|
|
|
|
|
¶y |
|
|
|
|||
+V |
|
¶Vx |
¶x |
|
|
¶p + μ × |
¶ Vx |
||||
|
= β × ρ × g × |
(t - t )- |
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
y |
|
|
|
|
|
∞ |
¶x |
|
¶x |
2 |
|
|
¶y |
|
|
|
|
|
|
|
||
+ ¶2V
x ,
¶ 2 y
(2.110)
(2.111)

16
|
¶Vy |
|
¶Vy |
|
|
|
¶p |
|
¶2Vy |
|
¶ |
2Vy |
|
|
||||||||||||||
|
|
|
+Vy |
|
|
|
|
= - |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ρ × Vx |
¶x |
|
|
|
|
|
¶y |
+ μ × |
¶x |
2 |
|
|
|
¶y |
2 |
|
||||||||||||
|
|
|
|
¶y |
|
|
|
|
+ |
¶ |
|
|
|
|
|
|||||||||||||
ρ ×c × V |
|
¶t +V |
|
¶t |
= λ × ¶ |
|
t |
|
|
t |
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
p x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
¶x |
|
|
|
|
|
|
2 |
|
|
¶y |
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
¶y |
¶x |
|
|
|
|
|
|
|
|
||||||||||||
(2.112)
(2.113)
Отметим, что уравнения (2.110) ÷ (2.113) относятся к эллиптическому типу и их решение требует задания граничных условий на всей замкнутой границе рассматриваемой области.
Тейлор и Карман определили турбулентность как «нерегулярное движение, которое, как правило, возникает в жидкости или газе при обтекании ими твёрдой поверхности или даже в случае соприкасания или перемешивания потоков одной и той же природы».
Определяющие уравнения для турбулентных течений характеризуются в общем случае сильной нелинейностью, а численные свойства нелинейных дифференциальных уравнений ещё недостаточно изучены. Для турбулентных течений справедливы те же уравнения сплошности, движения и энергии, которые описывают ламинарные течения. Единственное различие между соответствующими двумя системами уравнений заключается лишь в том, что при турбулентных течениях зависимые переменные (например, Vx, Vy, p и t) интерпретируются как мгновенные величины (при осреднении по времени), каждая из которых в соответствии с аппроксимирующим выражением представляется суммой осреднённого значения и пульсации, причём предполагается, что осреднения как по времени, так и по ансамблю эквивалентны (эргодическая гипотеза). Тогда подстановка аппроксимирующих соотношений в уравнения сплошности, движения и энергии, описывающие ламинарное двумерное течение несжимаемой жидкости в режиме естественной конвекции (2.110) ÷ (2.113) с учётом дифференцирования по времени даёт
|
|
|
|
|
|
|
|
|
|
|
|
|
¶V |
x + |
¶Vy |
= 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
DVx |
|
|
|
|
|
|
|
|
|
1 |
|
∂p |
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
= β × g |
× (t - t∞ )- |
|
× |
¶x + Ñ × (ν ×ÑVx )- |
|
|
|
vx ' |
- |
|
|
|
vx |
'vy |
', |
|||||||||||||||||||||||||||
Dτ |
ρ |
¶x |
¶y |
||||||||||||||||||||||||||||||||||||||||
|
|
DVy |
= - |
1 |
|
× |
¶p + Ñ ×(ν ×ÑV |
)- |
¶ |
|
|
|
|
|
|
|
|
|
¶ |
|
|
|
, |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
'2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
v |
|
|
'v |
|
|
'- |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Dτ |
|
|
|
|
|
¶y |
|
|
|
|
y |
|
|
|
¶x |
x |
|
y |
|
|
¶y y |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
Dt |
|
|
= Ñ × (a ×Ñt )- |
∂ |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
t'vx '- |
|
|
t'vy '. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
Dτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(2.114)
(2.115)
(2.116)
(2.117)
При выводе уравнений (2.114) ÷ (2.117) совершенно не учитывается влияние пульсаций плотности. Заметим, что если напряжения Рейнольдса
vx 'vy ' и корреляции второго порядка vx '2 и vy '2 стремятся к нулю, то урав-
нения (2.114) ÷ (2.117) сводятся к соответствующей системе уравнений для ламинарных течений. Эти напряжения и корреляции являются величинами, характеризующими именно турбулентные течения. Определение этих ве-
17
личин с достаточной точностью представляет собой серьёзную задачу при исследовании турбулентных течений.
Если не делать никаких предположений относительно корреляций осреднённых величин или не вводить для них дополнительных уравнений, то система уравнений (2.114) ¸ (2.117) остаётся незамкнутой. Для замыкания этой системы разработано несколько моделей, таких, как модель турбулентности нулевого, первого и второго порядков, а также приближённые теории замыкания более высоких порядков [213].
Система уравнений (2.110) ¸ (2.113) решалась численно методом конечных разностей. Для этой цели область течения, занимаемая жидкостью, разбивалась разностной сеткой с шагом (i,j), где i,j – индексы узлов сетки. Для примера разностная сетка для четырёх точек в начале координатных осей показана на рис.2.8.
Ниже приведены уравнения в конечно-разностном виде для точек, показанных на рис.2.7. При составлении уравнений использовались приведённые выше граничные условия.
При шаге по координатным осям 0,0001 м. получена система уравнений, которая в результате элементарных преобразований приведена к треугольной матрице, т. е. была решена. Система уравнений в матричном виде приведена ниже.
Уравнения (2.110) ÷ (2.113) для точек в конечно-разностном виде записываются следующим образом.
Точка (i,j):
V (i, j) − V (i − 1, j) |
+ |
Vy |
(i, j) − Vy (i, j − 1) |
= 0 |
, |
|
|
|
|
|
|
|
|
|
|
||||||||||
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V (i, j)× |
Vx (i, j)−Vx (i −1, j) |
+V (i, j)× |
Vx (i, j)−Vx (i, j−1) |
=b×g×(t |
|
-t )- |
1 |
|
× |
P(i, j)−P(i −1, j) |
+ |
||||||||||||||
|
|
|
|
r |
|
||||||||||||||||||||
x |
|
|
Dx |
|
|
|
|
|
y |
|
|
Dy |
|
i, j |
∞ |
|
|
Dx |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Vx (i -1, j)-2×Vx (i, j)+Vx (i +1, j) |
|
Vx (i, j-1)-2×Vx (i, j)+Vx |
(i, j+1) |
|
|
|
||||||||||||||||||
+n× |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
, |
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
|
Dx |
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
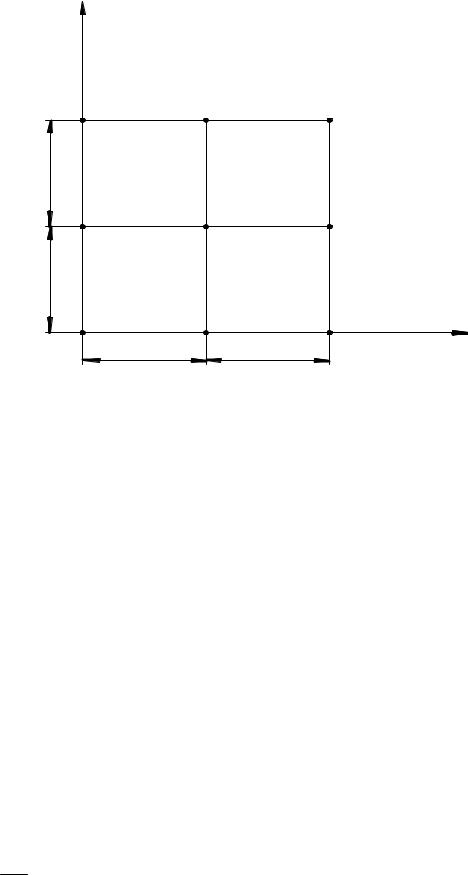
|
18 |
|
|
x, i |
|
|
|
i+1, j-1 |
i+1, j |
i+1, j+1 |
|
x |
|
|
|
i, j-1 |
i, j |
i, j+1 |
|
x |
|
|
|
i-1, j-1 |
i-1, j |
i-1, j+1 |
y, j |
|
|||
y |
|
y |
|
Рис. 2.8. Разбивка области разностной сеткой
V (i, j) × |
Vy (i, j) -Vy (i -1, j) |
+V (i, j) × |
Vy (i, j) -Vy (i, j -1) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
x |
|
|
|
|
|
|
Dx |
|
|
|
y |
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= - |
1 |
× |
P - P |
|
+ν |
|
V (i -1, j) - 2 ×V (i, j) +V (i +1, j) |
+ |
V (i, j -1) - 2 ×V (i, j) +V (i, j +1) |
|||||||||||||||||||||||||||||||||
|
|
i, j i, j −1 |
× |
|
|
|
|
y |
2 |
|
y |
|
|
|
|
|
|
y |
|
|
|
|
y |
2 |
|
y |
|
|
|
, |
||||||||||||
|
ρ |
|
|
Dy |
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
t |
i , j |
- t |
i −1, j |
|
|
|
|
t |
i, j |
- t |
i, j |
−1 |
|
t |
i −1, j |
- 2 × t |
i , j |
+ t |
i +1, j |
|
t |
i , j −1 |
- 2 × t |
i, j |
+ t |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i, j +1 |
|||||||||||||||
Vx |
(i, j) × |
|
|
|
|
|
|
+ Vy (i, j) × |
|
|
|
|
|
|
= a |
× |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
. |
||||||
|
|
Dx |
|
|
|
Dy |
|
|
|
|
|
Dx |
2 |
|
|
|
|
Dy |
2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В результате преобразований получаем
V (i, j) × |
1 |
+V (i, j) × |
1 |
= V (i -1, j) × |
1 |
+V (i, j -1) × |
|
1 |
. |
|
|
|
|
Dx |
Dy |
Dx |
|
|
|
|
|
|
|||||
x |
y |
x |
y |
Dy |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
При Vx (i -1, j ) = Vy (i, j -1) = 0 |
получаем: |
|
Vx (i, j) × |
1 |
+Vy (i, j) × |
1 |
= 0 , |
||||||
|
Dx |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Dy |
||
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
ν |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vx |
(i, j) × Vx |
'(i, j) × |
|
|
|
2 |
+ |
|
2 |
+Vy '(i, j) × |
|
|
|
-Vx |
(i +1, j) × |
|
|
|
2 -Vx |
||||||||||
Dx |
+ 2 ×ν × |
|
Dy |
|
|
|
Dx |
||||||||||||||||||||||
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|||||||||
+ |
P(i, j) × |
1 |
- ti, j |
× β × g = Vx (i - |
1, j) × |
|
|
'(i, j) × |
1 |
+ |
ν |
|
|
+Vx (i, j -1) |
× |
|
'(i, |
||||||||||||
|
|
Vx |
|
|
|
|
|
Vy |
|||||||||||||||||||||
ρDx |
Dx |
Dx |
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+ P(i -1, j) × ρ1Dx - β × g ×t∞ .
При Vx (i -1, j ) = Vx (i, j -1) = 0 получаем:
(i, j +1) × |
ν |
|
+ |
|||||
Dy2 |
||||||||
|
|
|
|
|
|
|||
j) × |
1 |
+ |
ν |
|
|
|
+ |
|
|
|
|
|
|
||||
Dy |
Dy |
2 |
|
|||||
|
|
|
|
|
|
|||
19
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 ×ν × |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Vx (i, j) × Vx '(i, j) × |
|
|
|
|
+ |
|
|
|
2 |
|
+ |
|
|
|
|
|
|
+Vy '(i, j) × |
|
|
|
|
-Vx (i +1, j) × |
|
|
2 -Vx (i, j +1) × |
|
2 + |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Dy |
2 |
|
|
|
|
|
Dx |
Dy |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
+ P(i, j) × |
1 |
|
|
- t × β × g = P(i -1, j) × |
|
|
1 |
|
|
- β × g ×t , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
ρDx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
i, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρDx |
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 ×ν × |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Vy |
(i, j) × Vx |
'(i, j) × |
|
|
|
+ Vy |
'(i, j) × |
|
|
|
+ |
|
|
|
|
2 + |
|
|
|
|
2 |
|
-Vy (i |
+1, j) × |
|
|
|
|
2 -Vy (i, j +1) × |
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dx |
Dy |
|
|
Dx |
|
Dy |
|
|
Dx |
|
Dy |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
ν |
|
|
|
|
|
1 |
|
|||||||||||
+ Pi, j × |
|
|
|
= Vy (i -1, j) × Vx |
'(i, j) × |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ Vy |
(i, j -1) × |
Vy '(i, j) × |
|
|
|
|
+ |
|
|
|
|
|
|
|
+ Pi, j −1 × |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
ρDy |
|
|
|
|
|
Dx |
2 |
|
Dy |
|
Dy |
2 |
ρDy |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
При Vy (i -1, j ) = Vy (i, j -1) = 0 |
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 ×ν × |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Vy |
(i, j) × Vx |
'(i, j) × |
|
|
|
+ Vy |
'(i, j) × |
|
|
|
+ |
|
|
|
|
2 + |
|
|
|
|
2 |
|
-Vy (i |
+1, j) × |
|
|
|
|
2 - |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Dx |
Dy |
|
|
Dx |
|
Dy |
|
|
Dx |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
-V |
(i, j +1) × |
|
|
|
|
|
+ P |
× |
|
|
1 |
|
= P |
−1 |
× |
1 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Dy2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
i, j |
|
|
ρDy |
|
|
|
|
i, j |
|
|
|
ρDy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ti, j |
× Vx '(i, j) × |
|
|
|
|
|
+ Vy '(i, j) × |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
+ |
|
|
|
|
|
|
2 |
|
- ti +1, j |
× |
|
2 - ti, j +1 |
× |
|
|
|
|
|
2 = |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
Dx |
|
Dy |
+ 2 × a × |
|
|
|
|
Dy |
|
|
Dx |
Dy |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= ti −1, j |
× Vx '(i, j) × |
|
|
|
|
|
+ |
|
|
|
|
|
+ ti, j −1 × Vy '(i, j) × |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Dx |
Dx |
2 |
Dy |
|
Dy |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
+
.
Точка (i+1,j):
V (i +1, j) -V (i, j) |
+ |
Vy |
(i +1, j) -Vy (i +1, j -1) |
= 0, |
|
|
|
|||||||||||||
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Dx |
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
||
V (i +1, j) × |
Vx (i +1, j) -Vx (i, j) |
+V (i +1, j) × |
Vx (i +1, j) -Vx (i +1, j -1) |
= |
|
|||||||||||||||
|
|
|
|
|
||||||||||||||||
|
x |
|
|
|
Dx |
|
y |
|
|
|
Dy |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= β × g × (ti +1, j |
- t∞ ) - |
1 |
× |
Pi +1, j - Pi, j |
+ |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
ρ |
Dx |
|
|
|
|
|
|
|
|||||
|
|
(i, j) |
- 2 ×Vx (i +1, j) +Vx (i + 2, j) |
|
Vx (i +1, j -1) - 2 ×Vx (i +1, j) +Vx (i +1, j +1) |
|
||||||||||||||
+ν × |
Vx |
+ |
, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
Dx |
|
|
|
|
|
Dy |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Vx (i +1, j) × |
Vy (i +1, j) -Vy (i, j) |
+Vy (i +1, j) × |
Vy (i +1, j) -Vy (i +1, j -1) |
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= - |
1 |
× |
P |
- P |
|
|
+ν × |
V (i, j) - 2 ×V (i +1, j) +V (i + 2, j) |
+ |
V (i +1, j -1) - 2 ×V (i +1, j) +V (i +1, j +1) |
||||||||||||||||||||||||||
|
i+1, j |
|
i +1, j −1 |
|
|
|
y |
|
2 |
|
|
|
|
y |
|
|
|
|
y |
2 |
y |
|
|
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ρ |
|
|
|
Dy |
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|||||
|
|
|
|
|
|
t |
- t |
i, j |
|
|
|
|
t |
i +1, j |
- t |
|
t |
|
- 2 ×t |
|
+ t |
+ 2, j |
|
|
t |
|
- 2 ×t |
|
+ t |
|
|
|||||
Vx (i +1, j) × |
|
i +1, j |
|
|
+Vy (i +1, j) × |
|
|
i +1, j −1 |
|
= a × |
i, j |
i+1, j |
i |
+ |
|
i +1, j −1 |
i+1, j |
i +1, j |
+1 |
|||||||||||||||||
|
Dx |
|
|
|
Dy |
|
|
|
|
Dx |
2 |
|
|
|
|
|
Dy |
2 |
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
20
В результате преобразований получаем
Vx (i +1, j) × |
1 |
|
+Vy (i +1, j) × |
1 |
|
|
-Vx (i, j) × |
1 |
|
= Vy (i +1, j -1) × |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
Dy |
|
|
Dx |
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|||||||
|
При Vy (i + 1, j − 1) = 0 |
|
|
|
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Vx (i +1, j) × |
1 |
|
+Vy (i +1, j) × |
1 |
|
|
-Vx (i, j) × |
|
1 |
= 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
Dy |
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
|
|
ν |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
ν |
|
|
2 ×ν |
|
|
|
-Vx |
(i, j) × Vx '(i +1, j) × |
|
+ |
|
|
|
+Vx (i +1, j) × Vx |
'(i +1, j) × |
|
|
+Vy |
'(i +1, j) × |
|
+ |
|
|
+ |
|
|
|
- |
||||||||||
Dx |
|
|
2 |
Dx |
|
Dy |
Dx |
2 |
Dy |
2 |
|||||||||||||||||||||
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
-V (i +1, j +1) × |
|
ν |
|
|
|
+ P(i +1, j) × |
1 |
|
|
|
- P(i, j) × |
|
|
1 |
|
|
- t |
|
× β × g = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
Dy2 |
|
ρDx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρDx |
|
|
|
i +1, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= V (i +1, j -1) × V |
|
'(i +1, j) × |
1 |
|
+ |
ν |
- β × g ×t |
∞ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
Dy |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
При Vx (i + 1, j −1) = 0 получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ν |
|
|
|
|
|
|
2 ×ν |
|
|
|
|
|
|
|
||||||||||||
-Vx |
(i, j) × Vx |
'(i +1, j) × |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ Vx |
|
(i +1, j) × Vx '(i +1, j) × |
|
|
|
|
+ Vy |
'(i |
+1, j) × |
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
- |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Dx |
Dx |
2 |
|
Dx |
|
Dy |
|
Dx |
2 |
|
Dy |
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
-Vx (i +1, j + |
1) × |
|
|
|
|
|
+ P(i |
+1, j) × |
|
1 |
|
|
- P(i, j) × |
|
1 |
|
- ti +1, j × β × g = -β × g × t∞ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dy2 |
|
|
|
|
|
ρDx |
ρDx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ν |
|
|
|
|
|
|
2 ×ν |
|
|
|
|
|
|
|
|
|||||||||
-Vy |
(i, j) × Vx |
'(i +1, j) × |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ Vy |
|
(i +1, j) × Vx '(i +1, j) × |
|
|
|
+ Vy |
'(i |
+1, j) × |
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
- |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Dx |
|
|
Dx |
2 |
Dx |
Dy |
|
Dx |
2 |
|
|
Dy |
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
-Vy (i +1, j + |
1) × |
|
|
|
|
|
|
+ P(i |
+1, j) × |
|
|
|
|
|
|
|
= Vy (i +1, j -1) × Vy '(i |
+1, j) × |
|
|
|
|
+ |
|
|
|
|
|
+ P(i +1, j -1) × |
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dy |
2 |
|
|
|
|
ρDy |
|
Dy |
Dy |
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρDy |
|
|
|
||||||||||||||
|
При Vy (i + 1, j −1) = 0 получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ν |
|
|
|
|
|
|
2 ×ν |
|
|
|
|
|
|
|
|
|||||||||
-Vy |
(i, j) × Vx |
'(i +1, j) × |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ Vy |
|
(i +1, j) × Vx '(i +1, j) × |
|
|
|
+ Vy |
'(i |
+1, j) × |
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
- |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Dx |
|
|
Dx |
2 |
Dx |
|
|
Dy |
|
Dx |
2 |
|
|
Dy |
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
-Vy (i +1, j + |
1) × |
|
|
|
|
+ P(i |
+1, j) × |
1 |
|
|
= P(i +1, j |
-1) × |
|
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Dy2 |
|
|
|
ρDy |
|
ρDy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
a |
|
|
|
|
|
2 × a |
|
|
|
|
|
|
a |
|
|
|||||||||||||||||||
- ti, j × Vx |
'(i +1, j) × |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ ti +1, j |
|
× Vx '(i +1, |
|
j) × |
|
|
|
|
+ Vy |
'(i +1, j) × |
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
- ti +1, j +1 × |
|
|
= |
|||||||||||||||||||||||||||||||||||||||
Dx |
|
|
|
Dx |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
2 |
|
|
Dy |
2 |
Dy |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
= ti +1, j −1 × |
|
'(i +1, |
|
|
|
|
× |
1 |
|
|
|
+ |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Vy |
|
j) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Dy |
|
Dy |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Точка (i,j+1):
