
6882
.pdf21
|
|
|
|
1 |
|
ν |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
2 ×ν |
|
ν |
|
|
|
|
-Vy |
(i, j) × Vy |
'(i, j +1) |
× |
|
+ |
|
|
|
+ Vy |
(i, j +1) × Vx |
'(i, j +1) |
× |
|
+ Vy |
'(i, j +1) |
× |
|
+ |
|
|
+ |
|
|
|
- |
Dy |
Dy |
2 |
Dx |
Dy |
Dx |
2 |
Dy |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
||||||||
-Vy (i +1, j + |
1) × |
|
|
|
|
|
+ P(i, j |
|
|
+1) × |
|
|
|
|
|
- P(i, j) × |
|
|
|
|
|
|
|
|
= Vy (i -1, j +1) × Vx |
'(i, j +1) |
× |
|
|
|
|
|
|
+ |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dx |
2 |
|
|
|
|
ρDy |
|
|
ρDy |
Dx |
|
Dx |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
При Vy (i −1, j + 1) = 0 получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
2 ×ν |
|
|
|
ν |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
-Vy (i, j) × Vy |
'(i, j +1) × |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ Vy (i, j +1) × Vx |
'(i, j + |
1) × |
|
|
+ Vy '(i, j +1) × |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
- |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dy |
|
|
Dy |
2 |
|
|
|
Dx |
|
Dy |
|
Dx |
2 |
Dy |
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
-Vy (i +1, j + |
1) × |
|
|
|
|
+ P(i, j |
+1) × |
|
|
1 |
|
|
- P(i, j) × |
|
|
1 |
|
|
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dx2 |
|
|
|
ρDy |
|
ρDy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- t × V '(i, j +1) × |
|
|
1 |
+ |
|
|
|
|
a |
+ t |
|
|
|
|
× V '(i, j +1) × |
|
|
1 |
|
+V '(i, j +1) × |
1 |
+ |
2 × a |
+ |
|
a |
- t |
|
|
|
|
|
|
× |
|
a |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
2 |
|
|
|
|
|
|
|
|
i, j +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
y |
|
|
|
Dy |
|
Dx |
2 |
|
|
|
|
Dy |
|
|
|
|
|
i +1, j +1 |
|
|
Dx |
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= ti −1, j +1 × |
Vx '(i, j +1) × |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Dx |
|
Dx |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Точка (i+1,j+1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
V (i +1, j +1) -V (i, j +1) |
+ |
Vy (i +1, j +1) -Vy |
(i +1, j) |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
V (i +1, j +1) × |
Vx (i +1, j +1) -Vx (i, j +1) |
+V (i +1, j +1) × |
Vx (i +1, j +1) -Vx (i +1, j) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= β × g × (t |
|
|
|
|
- t ) - |
|
1 |
|
× |
Pi +1, j +1 - Pi, j +1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
i +1, j +1 |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vx (i +1, j) - 2 ×Vx (i +1, j +1) +Vx (i +1, j + |
2) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
+ν × |
Vx (i, j +1) - 2 ×Vx (i +1, j +1) +Vx (i + 2, j +1) |
+ |
, |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
V (i +1, j +1) -V (i, j +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V (i +1, j +1) -V (i +1, j) |
|
|
|
|
|
1 |
|
|
P |
|
|
+1 |
- P |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
V (i +1, j +1) × |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
+V (i +1, j +1) × |
y |
|
|
|
y |
|
|
|
|
|
|
|
= - |
|
|
|
|
|
× |
|
i+1, j |
|
|
|
i+1, j |
+ |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
Dy |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ν × |
V (i, j +1) - 2×V (i +1, j +1) +V (i + 2, j +1) |
|
|
V (i +1, j) - 2×V (i +1, j +1) +V (i +1, j + 2) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
V (i +1, j +1) × |
ti +1, j +1 - ti, j +1 |
|
|
|
+V (i +1, j +1) × |
ti +1, j +1 |
|
- ti +1, j |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
t |
|
+1 |
- 2 ×t |
|
|
2 |
|
|
+ t |
i + 2, j +1 |
|
+ |
|
t |
i +1, j |
|
- 2 ×t |
|
|
2 |
|
|
|
+ t |
i +1, j + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
= a × |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
i, j |
|
|
|
|
|
|
i +1, j |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i +1, j +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В результате преобразований получаем:
V (i +1, j +1) × |
1 |
-V (i, j +1) × |
1 |
+V (i +1, j +1) × |
1 |
-V (i +1, j) × |
1 |
= 0, |
Dx |
Dx |
Dy |
|
|||||
x |
x |
y |
y |
Dy |
||||
|
|
|
|
|
||||
22
|
|
|
|
1 |
|
|
|
1 |
|
ν |
|
|
ν |
|
|
|
|
|
|
1 |
|
ν |
|
|
|
Vx |
(i +1, j +1) × Vx |
'(i +1, j +1) |
× |
|
+Vy |
'(i +1, j +1) |
× |
|
+ |
|
|
+ |
|
|
|
-Vx |
(i, j +1) × Vx |
'(i +1, j +1) |
× |
|
+ |
|
|
|
- |
Dx |
Dy |
Dx |
2 |
Dy |
2 |
Dx |
Dx |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-V (i +1, j) × V '(i +1, j +1) × |
|
|
|
1 |
+ |
|
ν |
|
|
+ P(i +1, j +1) × |
1 |
|
|
- P(i, j +1) × |
1 |
|
-t |
|
× β × g = -β × g ×t , |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Dy |
|
ρDx |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
Dy |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρDx |
i +1, j +1 |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ν |
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
ν |
|
|
|
|
|||||||
Vy (i +1, j +1) × |
Vx '(i +1, j |
+1) |
|
× |
|
|
|
|
|
+Vy '(i +1, j +1) × |
|
|
|
+ |
|
|
|
|
|
+ |
|
|
-Vy (i, j |
+1) × Vx '(i +1, j +1) × |
|
|
|
+ |
|
|
|
|
|
|
- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Dx |
2 |
Dy |
2 |
Dx |
|
Dx |
2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
|
|
Dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
-Vy (i +1, j) × Vy '(i +1, j +1) × |
|
|
|
|
|
+ |
|
|
|
|
|
+ P(i +1, j +1) × |
|
|
|
|
|
- P(i +1, j) × |
|
|
|
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Dy |
|
Dy |
2 |
|
|
ρDy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρDy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
a |
|
|
|
|
|||||||
ti +1, j +1 |
× Vx '(i |
+1, j +1) × |
|
|
|
|
|
+Vy '(i +1, j +1) × |
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
- ti, j +1 × Vx |
'(i |
+ |
1, j +1) × |
|
|
|
+ |
|
|
|
|
|
- |
||||||||||||||||||||||
Dx |
|
|
Dy |
Dx |
2 |
|
Dy |
2 |
|
|
|
Dx |
2 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dx |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- ti +1, j |
× Vy '(i +1, j +1) |
× |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Dy |
|
Dy |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В матричном виде система уравнений для четырёх рассматриваемых точек имеет вид A × X = B , где А – матрица коэффициентов, Х – матрица неизвестных величин, В – матрица свободных членов.
23
|
4 |
|
4 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
10 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
6770 |
|
0 |
|
−1498 |
|
0 |
|
−1498 |
|
0 |
|
0 |
|
0 |
|
−0.7 |
|
0 |
|
0 |
|
0 |
|
8265 |
|
0 |
|
0 |
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
|
6770 |
|
0 |
|
−1498 |
|
0 |
|
−1498 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
8265 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
9223 |
|
−2111 |
|
−2111 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
−104 |
|
0 |
|
104 |
|
104 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1498 |
|
|
|
|
|
−0.7 |
|
|
|
|
|
−8265 |
|
|
|
|
|
|
||
−1988 |
|
0 |
|
5473 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
0 |
|
|
0 |
|
0 |
|
|
8265 |
|
0 |
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
−1988 |
|
0 |
|
5473 |
|
0 |
|
0 |
|
0 |
|
−1498 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
8265 |
|
0 |
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2601 |
|
|
|
|
|
−2111 |
|
|
|
|
|
|
|
|
||
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
7313 |
|
0 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
||
A= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
0 |
|
4 |
|
0 |
|
0 |
|
4 |
|
4 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
||
|
|
−10 |
|
|
|
10 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
938 |
|
0 |
|
0 |
|
0 |
|
5613 |
|
0 |
|
−1498 |
|
0 |
|
0 |
|
0 |
|
−0.7 |
|
0 |
|
0 |
|
0 |
|
8265 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
938 |
|
0 |
|
0 |
|
0 |
|
5613 |
|
0 |
|
−1498 |
|
0 |
|
0 |
|
0 |
|
0 |
|
−8265 |
|
0 |
|
8265 |
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
−2671 |
|
0 |
|
7453 |
|
−2111 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−104 |
|
−104 |
|
|
|
104 |
|
104 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
0 |
|
0 |
|
|
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
−2238 |
|
0 |
|
−2238 |
|
0 |
|
4475 |
|
0 |
|
0 |
|
0 |
|
0 |
|
−0.7 |
|
0 |
|
0 |
|
−8265 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8265 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2238 |
|
|
|
−2238 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−8265 |
|
|
|
|
||
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
0 |
|
4475 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
8265 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
−2851 |
|
−2851 |
|
5702 |
|
0 |
|
0 |
|
0 |
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
24
|
Vx (i, j) |
|
||
|
Vy (i, j) |
|
||
|
|
|||
|
Vx (i + 1, j) |
|
||
|
Vy |
(i + 1, j) |
|
|
|
|
|||
|
V |
(i, j + 1) |
|
|
|
x |
|
|
|
Vy (i, j + 1) |
||||
|
|
|||
V (i + 1, j + 1) |
||||
|
x |
|
|
|
Vy (i + 1, j + 1) |
||||
X = |
|
ti, j |
; |
|
|
|
|
||
|
|
ti +1, j |
|
|
|
|
ti, j +1 |
|
|
|
|
|
||
|
ti +1, j +1 |
|
||
|
|
|||
P(i, j) |
||||
|
|
|||
|
P(i + 1, j) |
|
||
|
P(i, j + 1) |
|
||
|
|
|||
|
|
|
|
|
P(i + 1, j + 1)
|
0 |
|
|
|
|
|
|
1164000 |
|
||
7899000 |
|||
|
272600 |
|
|
|
|
||
|
0 |
|
|
|
− 9.807 |
|
|
|
|
||
7899000 |
|||
|
|
|
|
46550 |
|
||
B = |
0 |
. |
|
|
|
||
|
|||
1164000 |
|
||
|
0 |
|
|
|
|
||
|
37390 |
|
|
|
0 |
|
|
|
|
||
|
− 9.807 |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
||
25
В результате преобразований получена треугольная матрица коэффициентов и свободных членов:
104 |
|
104 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
4 |
|
0 |
|
0 |
|
4 |
|
4 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
0 |
||||
|
|
-10 |
|
|
|
10 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
0 |
|
0 |
|
104 |
|
104 |
|
104 |
|
104 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-104 |
|
-104 |
|
|
|
104 |
|
104 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||
0 |
|
0 |
|
0 |
|
|
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
0 |
|
8268 |
|
5272 |
|
-1498 |
|
-1498 |
|
0 |
|
0 |
|
0 |
|
0 |
|
8265 |
|
0 |
|
0 |
|
0 |
7899000 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
5951 |
|
169 |
|
-1329 |
|
0 |
|
0 |
|
0 |
|
0 |
|
-9203 |
|
0 |
|
8265 |
|
0 |
|
|
-896100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2615000 |
||
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
-11951 |
|
- 6177 |
|
0 |
|
- 0.7 |
|
0 |
|
0 |
|
-17610 |
|
8265 |
|
6608 |
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 5369 |
|
- 9477 |
|
|
|
|
|
||||
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
2721 |
|
0 |
|
0.101 |
|
0 |
|
0 |
|
|
|
4146 |
|
8265 |
|
- 2312000 |
|||||
A = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; B = |
|
. |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
9223 |
|
- 2111 |
|
- 2111 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
272600 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
6717 |
|
-596 |
|
- 2111 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
123440 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2303 |
|
|
|
|
|
|
|
|
127590 |
||||
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
6787 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
|
|
|||
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
3752 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
110750 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-107 |
|
-85 |
|
||||
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
16537 |
|
116 |
|
|
|
|
8993030 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.072×107 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
15039 |
|
- 3338 |
|
- 3444 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 673 |
|
||||
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
13107 |
|
|
1194220 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10101 |
- 3062470 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
27 |
|
|
|
|
В результате расчёта математической модели получен базовый мате- |
||||||||
риал для описания процессов свободной конвекции около вертикальной |
||||||||
стенки с переменными граничными условиями. Результаты вычислений при- |
||||||||
ведены в графической форме рис.А.1.- А.4). |
|
|
|
|
||||
0.987 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
U6( x6, y6) |
|
|
|
|
|
|
|
|
U5( x5, y5) |
|
|
|
|
|
|
|
|
U4( x4, y4) |
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U3( x3, y3) |
|
|
|
|
|
|
|
|
U2( x2, y2) |
|
|
|
|
|
|
|
|
U1( x1, y1) |
|
|
|
|
|
|
|
|
U01( x01, y01) |
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U001( x001, y001) |
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0.002 |
0.004 |
0.006 |
0.008 |
0.01 |
0.012 |
0.014 |
|
|
0 |
|||||||
|
0 |
|
|
y6, y5, y4, y3, y2, y1, y01, y001 |
|
|
0.014 |
|
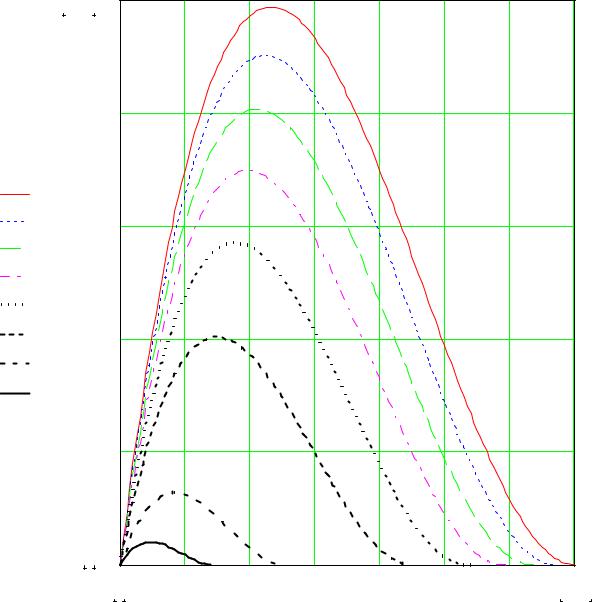
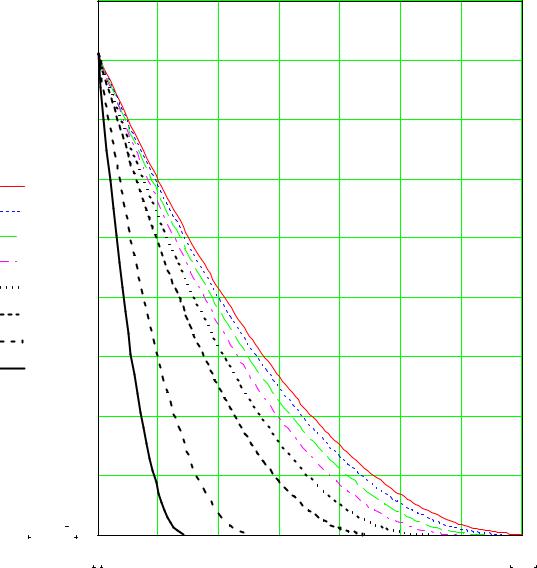
Рис. А.1. Профиль скорости Vx(x,y) около нагретой изотермической |
||||||||
|
|
|
|
пластины. |
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
90 |
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
θ6( x6, y6) |
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ5( x5, y5) |
|
|
|
|
|
|
|
|
|
|
θ4( x4, y4) |
|
|
|
|
|
|
|
|
|
|
θ3( x3, y3) |
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ2( x2, y2) |
|
|
|
|
|
|
|
|
|
|
θ1( x1, y1) |
|
|
40 |
|
|
|
|
|
|
|
θ01( x01, y01) |
|
|
|
|
|
|
|
|
|
|
θ001( x001, y001) |
30 |
|
|
|
|
|
|
|
||
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
. |
|
5 |
|
|
|
|
|
|
|
|
3.91510 |
|
0 |
0.002 |
0.004 |
0.006 |
0.008 |
0.01 |
0.012 |
0.014 |
|
|
|
|
0 |
|||||||
|
|
|
0 |
|
|
y6, y5, y4, y3, y2, y1, y01, y001 |
|
|
0.014 |
|
Рис. А.2. Профиль относительной температуры ϑ (x,y) около |
|
|||||||||
|
|
|
нагретой изотермической пластины. |
|
|
|
||||
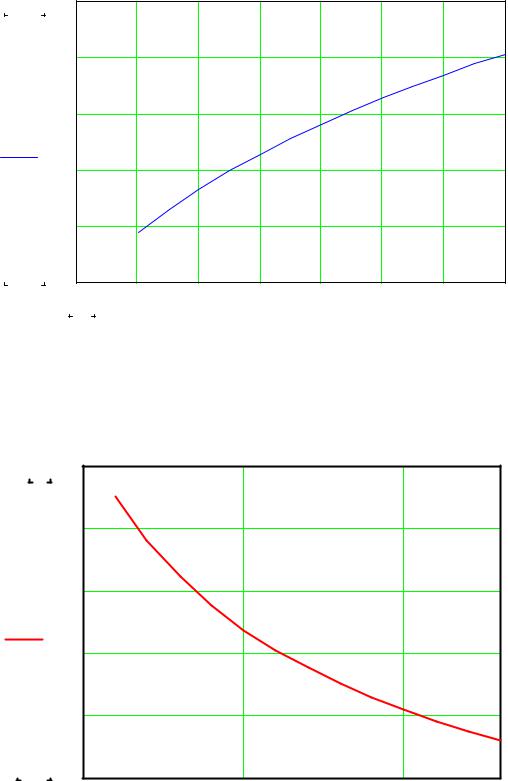
|
|
|
|
29 |
|
|
|
1.605 |
1.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.6 |
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
U ( x ) |
|
|
|
|
|
|
|
|
1.4 |
|
|
|
|
|
|
|
1.3 |
|
|
|
|
|
|
1.288 |
1.2 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
|
|||||||
|
0.4 |
||||||
|
0.6 |
|
|
|
x |
|
1.8 |
Рис. А.3. Профиль скорости Vx max около адиабатической стенки. |
|||||||
95 |
100 |
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
T ( x ) |
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
55.9 |
50 |
|
|
1 |
|
|
1.5 |
|
|
|
|
|
|||
|
0.5 |
|
|
|
|
||
|
0.5 |
|
|
|
x |
|
1.8 |
Рис. А.4. Профиль температуры Tas(x) на адиабатической стенке. |
|||||||
30
2.Основы теории подобия. Моделирование тепловых
игидро-аэродинамических процессов
2.1. Основы теории подобия
При обтекании здания потоком воздуха около него образуется застойная зона. Определение размеров этой зоны, условий циркуляции в ней воздушных потоков и, следовательно, условий проветривания зоны также является целью аэродинамического исследования здания. Наибольшее значение это исследование имеет для промышленных зданий с большим количеством вредных выбросов.
На лобовых поверхностях здания вследствие торможения потока происходит преобразование кинетической энергии – энергии движения – в потенциальную энергию давления. Распределение давления на здании зависит от направления ветра (по отношению к зданию) и от того, открыто здание для воздействия ветра или защищено другими зданиями и вследствие этого находится в аэродинамической тени. Величина давления в той или иной точке, кроме того, зависит от скорости ветра.
Если здание загорожено, например, впереди него имеется такое же параллельно расположенное здание, то давления на втором по потоку здании будут зависеть от расстояния между зданиями.
При моделировании обычно принимается здание отдельно стоящим, что дает возможность переносить полученные данные на целый класс явлений. При исследовании же внешней аэродинамики конкретного здания необходимо детальное соблюдение всех критериев и параметров, влияющих на условия его обтекания воздушным потоком.
Для изучения давления ветра на твердые тела необходимо знать распределение аэродинамических сил по поверхности тел [2, 3]. Для установления основных закономерностей рассмотрим обтекание пластинки, расположенной перпендикулярно направлению воздушного потока, согласно методике Э.И.Реттера [2, 3] (рис. 1).
Выделим малую струйку и запишем для нее уравнение Бернулли, рассматривая сечения 0-0 и 1-1,
ρ × vo2 |
+ P = |
ρ × v12 |
+ P . |
(2.1) |
|
|
|||
2 |
o |
2 |
1 |
|
|
|
|
Если сечение 0-0 взято на достаточном расстоянии от пластинки, то vо будет представлять скорость невозмущенного потока, и тогда Ро=Рат – атмосферные давления. Член r×vо2/2 представляет собой кинетическую энергию невозмущенного потока (скоростной напор).
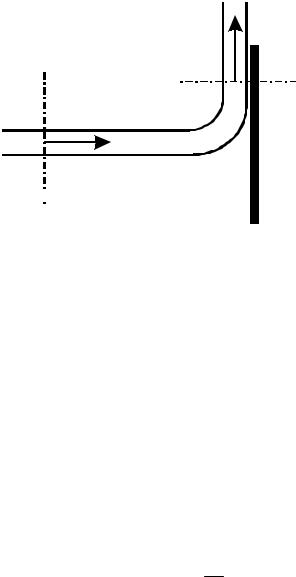
31
v1
0 |
v0 |
1 |
1 |
|
0 
Рис. 2.1. Схема обтекания пластинки, расположенной перпендикулярно направлению воздушного потока.
Тогда последнее выражение перепишется следующим образом
P1 - Pат |
= |
ρ × vo2 |
- |
ρ × v12 |
. |
(2.2) |
||||
|
|
|
||||||||
Или в другом виде |
2 |
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
P1 - Pат |
= |
ρ× vo2 |
× (1- |
v12 |
). |
|
(2.3) |
|||
|
v2 |
|
||||||||
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
o |
|
|
|
Левая часть полученного выражения – это избыточное давление Рi в сечении 1-1 по сравнению с атмосферным давлением Рат.
Из изложенного следует, что избыточное давление в произвольно выбранном сечении пропорционально скоростному напору. Выражение в скобках представляет собой аэродинамический коэффициент сv
2
сv = 1− v12 . (2.4) vo
Тогда избыточное давление в точке замера на поверхности здания определится из выражения
Pi |
= сv |
× |
ρ× vo2 |
. |
(2.5) |
|
|||||
|
|
2 |
|
|
|
Таким образом, аэродинамический коэффициент сv определяет ту долю скоростного давления, которая переходит в статическое давление при обтекании поверхности здания.
Полученное выражение является основным для оценки аэродинамических характеристик зданий. Избыточное давление при этом может быть отрицательным. Значение аэродинамического коэффициента лежит в следующих пределах: (-2)≤сv≤1.
Зная аэродинамическую характеристику здания в виде спектра распределения аэродинамических коэффициентов на его поверхности при
