
6882
.pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
Кочев А.Г.
МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В СИСТЕМАХ ТЕПЛОГАЗОСНАБЖЕНИЯ И ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ
Учебно-методическое пособие по подготовке к практическим занятиям
(включая рекомендации по выполнению расчётно-графической и самостоятельной работы)
для обучающихся по заочной форме по дисциплине «Моделирование процессов в системах теплогазоснабжения и планирование экспериментальных исследований» по направлению подготовки 08.04.01 Строительство
профиль Теплогазоснабжение населенных мест и предприятий
Нижний Новгород ННГАСУ
2016 г
2
УДК 726.5+536.24 (075.8)
Кочев А.Г. / Моделирование процессов в системах теплогазоснабжения и планирование экспериментальных исследований . [Электронный ресурс]: учеб.-метод. пос. / А.Г. Кочев; Нижегор. гос. архитектур. - строит. ун-т – Н. Новгород: ННГАСУ, 2016. – 53 с.–
1электрон. опт. диск (CD-RW).
Внастоящем учебно-методическом пособии по дисциплине «Моделирование процессов в системах теплогазоснабжения и планирование экспериментальных исследований» даются конкретные рекомендации учащимся для освоения основного и дополнительного материала дисциплины для достижения целей, обозначенных в учебной программе дисциплины. Цель учебно-методического пособия — помощь в подготовке к практическим занятиям, в освоении требуемого объёма знаний самостоятельной работы студентов, а также в написании расчётно-графической работы.
Учебно-методическое пособие предназначено для обучающихся по заочной форме в ННГАСУ по дисциплине «Моделирование процессов в системах
теплогазоснабжения и |
планирование экспериментальных |
исследований» |
по |
направлению подготовки |
08.04.01 Строительство, профиль |
Теплогазоснабжение |
|
населенных мест и предприятий |
|
|
|
Учебно-методическое пособие ориентировано на обучение в соответствии с календарным учебным графиком и учебным планом по основной профессиональной образовательной программе направления 08.04.01 Строительство, профиль Теплогазоснабжение населенных мест и предприятий, утверждённым решением научно-технического совета (НТС) ННГАСУ от 9.06.2015г. (протокол № 2).
© |
А.Г. Кочев, 2016 |
© |
ННГАСУ, 2016 |
|
3 |
|
|
Содержание |
|
|
Введение |
5 |
1. |
1. Методы термодинамического и физико-математического описа- |
|
|
ния процессов в системах ТГС |
5 |
|
1.1. Уравнение Лапласа |
6 |
|
1.2. Решения задач на вдув. Уравнение Фурье |
12 |
|
1.3. Численное моделирование теплообменных процессов |
15 |
2. |
Основы теории подобия. Моделирование тепловых и гидро- |
|
|
аэродинамических процессов |
30 |
|
2.1. Основы теории подобия |
30 |
|
2.2. Критерии (числа) подобия |
32 |
|
2.3. Степень турбулентности потока. Миделевое сечение |
35 |
|
2.4. Аэролинамические трубы и гидролотки |
36 |
3. |
Статистический анализ эксперимента. Планирование эксперимен- |
|
|
тальных исследований |
41 |
|
Библиографический список |
47 |
4. |
Порядок выполнения расчётно-графической работы |
48 |
5. |
Вопросы для контрольных работ |
51 |
4
ВВЕДЕНИЕ
В процессе передачи тепла через светопропускающее ограждение от внутреннего воздуха к наружному участвуют одновременно три вида теплообмена (теплопроводность, конвекция, излучение), которые влияют друг на друга. Для математического описания процесса переноса тепла при стационарном режиме можно использовать дифференциальные уравнения теплопроводности и конвекции (уравнение Лапласа).
Решение поставленной задачи возможно путем экспериментальных исследований и путем теоретического изучения законов формирования температурных полей на основе решения описывающих процесс математических уравнений.
Экспериментальный метод носит конкретный, и поэтому ограниченный характер. Для того чтобы сделать обобщение, необходимы результаты многих опытов. Экспериментальный метод чрезвычайно трудоёмок и требует длительных усилий для достижения конечной цели, но он является наиболее точным.
Путь аналитических исследований более универсален и связан с меньшими материальными и трудовыми затратами. Варьируя параметры задачи, можно получить решения для широкого диапазона толщин стен и различных сочетаний внутренних и внешних воздействий.
Методы термодинамического и физико-математического описания процессов в тепломассообменных аппаратах систем ТГВ выполняются с использованием теории подобия. В данном курсе рассматриваются ламинарные и турбулентные течения в инженерных приложениях, а также методы статистического анализа эксперимента. Приводятся основные методы планирования экспериментальных исследований и моделирование гидравлических явлений.
1. Методы термодинамического и физико-математического описания процессов в системах ТГС.
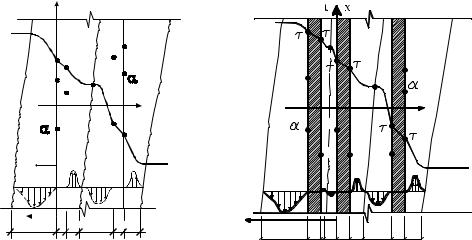
Передача теплоты через светопропускающее ограждение является сложной теплофизической задачей. Она осложнена наличием неоднородных элементов оконного блока, его сопряжением с наружной ограждающей конструкцией, фильтрацией воздуха, изменением теплофизических свойств в воздушной прослойке в зависимости от температурно-влажностных условий наружной и внутренней сред. В общем виде должна решаться нелинейная задача теплопередачи через окно. Общее сопротивление теплопередаче окна по остекленной части записывается как сумма слагаемых (рис. 1.1)
Ro = R в + ΣRст + R вп + R н. |
(1.1) |
Теплозащитные качества светопропускающих ограждений в основном зависят от термического сопротивления воздуха у внутренней
5
поверхности остекления Rв и термического сопротивления воздушных прослоек Rвп. В окнах с двойным остеклением термическое сопротивление Rв составляет 30÷35 % от общего сопротивления теплопередаче, термическое сопротивление Rвп составляет 45÷55 %. При тройном остеклении Rв составляет 20÷25 %, Rвп составляет 60÷70 %. Наибольшую трудность при определении Rв и Rвп представляет конвективная составляющая теплового потока.
|
t |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
t В |
|
|
|
|
|
|
tВ |
|
1 |
|
|
|
|
|
|
|
|
|
|
FН |
|
|
В |
|
|
|
|
|
|
||
|
τВ |
τ1 |
F2 |
|
|
|
|
tСР1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FН |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
FВ |
|
|
|
|
|
|
FВ |
2 |
|
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
tСР ОК |
|
Н |
|
|
|
|
|
tСР2 |
|
|
Н |
||
|
q |
F1 |
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
τ 2 |
|
τН |
|
|
B |
F2 |
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
4 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
vy |
|
|
|
|
t Н |
|
|
F1 |
|
F3 |
F4 |
|
|
|
|
vx |
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
y |
R1 |
R*ВП |
R**ВП |
R2 |
RН |
|
|
|
|
|
|
|
|
|
|
R В |
y |
Rв |
R 1 |
R''R |
|
R''' R'''' R |
|
R |
|
||||||
|
|
|
|
|
|
2 |
3 |
н |
|||||||
|
|
|
|
|
|
|
|
|
вп |
вп |
вп |
|
|||
|
|
|
|
|
|
|
|
R' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вп |
|
|
|
|
|
|
Рис. 1.1 Схема передачи теплоты через остекление оконного проема
Аналитических исследования при изучении теплопередачи белее универсальны и менее затратми. Варьируя параметры задачи, можно получить решения для широкого диапазона толщин стен и различных сочетаний внутренних и внешних воздействий.
К недостаткам можно отнести определенную общность, схематичность и субъективизм, которые в большей или меньшей степени присущи всем аналитическим моделям. Кроме того, часть факторов остаются за пределами модели как в силу их второстепенности, так и, возможно, в силу недостаточной изученности. Поэтому теоретические модели должны согласовываться с экспериментальными данными и проверяться ими.
В этой связи представляется, что более рациональным является путь аналитических исследований теплового режима оконных откосов в сочетании с экспериментальной проверкой физико-математической модели, используемой для расчетов и анализа реальных процессов.
1.1. Уравнение Лапласа
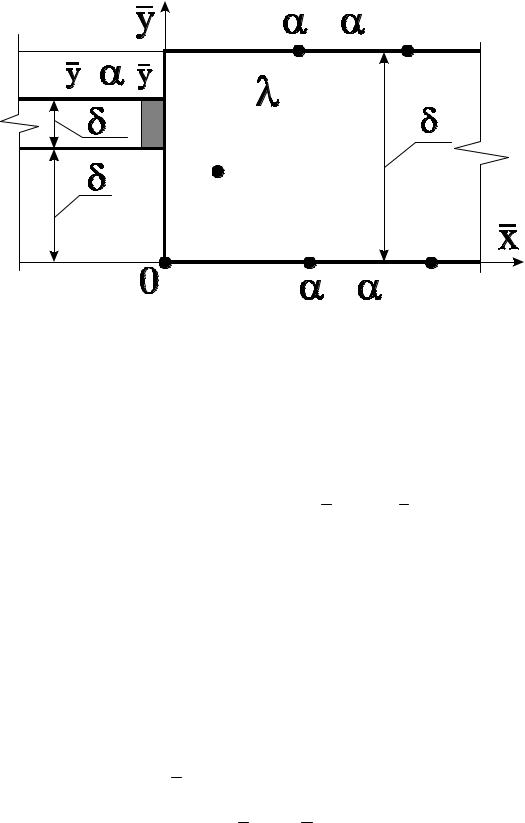
Для аналитического решения задачи нахождения температурного поля стены с постоянными физическими свойствами, примыкающей к оконному проему, была выбрана следующая физико-математическая модель, поясняемая рис. 1.2
6
t н= tж2 |
2 = н t пов н |
tж( ), ( ) |
|
ОК |
о |
t(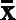 ;
;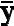 )
)
tв= tж1 |
1 = в t пов в |
Рис. 1.2. Схема расчетной области исследований
Задача решается для двумерного поля температур в стационарных условиях, т. е. требуется решить дифференциальное уравнение Лапласа:
¶ |
2 |
t |
+ |
¶ |
2 |
t |
= 0 . |
(1.2) |
|
|
2 |
|
|
2 |
|||
|
|
|||||||
¶x |
¶y |
|
||||||
Задача решается в следующих пределах: x > 0; 0 < y < δо .
Чтобы найти численные значения температур (температурное поле) сразу внутри и на поверхности исследуемой области, необходимо знать краевые условия – размеры и геометрию исследуемой области, теплофизические характеристики применяемых материалов и закон взаимодействия между окружающей средой и поверхностью области (граничные условия).
Записываем граничные условия:
|
¶t( |
|
|
|
|
|
|
= α × [t |
ж1 - t( |
|
,0)] |
|
|
|
|
|||||||||||
- λ × |
|
|
x,0) |
|
|
|
|
|||||||||||||||||||
|
|
x |
; |
|
(1.3) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
1 |
||||||||||||||||||||||
|
|
|
|
¶y |
2 × [t( |
|
|
,δo )- t |
ж2 ] ; |
|
||||||||||||||||
|
¶t( |
|
|
,δo ) = α |
|
|
||||||||||||||||||||
- λ × |
x |
|
||||||||||||||||||||||||
x |
(1.4) |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
¶y |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
¶t(0, |
|
) = α( |
y) × [t |
ж (y) - t(0, |
|
)] ; |
|
||||||||||||||||||
- λ × |
y |
|
||||||||||||||||||||||||
y |
(1.5) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||

7
|
|
|
|
|
|
t ж1 - t ж2 |
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
||||
t(¥, y) = t ж1 |
- |
|
|
|
|
× ( |
|
+ |
) |
. |
(1.6) |
|||||||
|
|
|
δо |
|
|
|
λ |
|
||||||||||
|
|
|
|
1 |
+ |
+ |
1 |
|
|
|
|
α1 |
||||||
|
|
|
|
|
α1 |
λ |
α2 |
|
|
|
|
|
|
|||||
Граничное условие (1.6) отвечает стационарному одномерному полю температуры вдали от оконного проема.
Принимается, что температура внутреннего воздуха tв, коэффициент теплоотдачи αв отк и градиент температуры в поперечном сечении откоса являются постоянными величинами. Потерями тепла через верхние и нижние части откоса пренебрегаем.
Температура tж (y) является известной функцией изменения температуры воздуха, ограничивающего поверхность оконного откоса и
наружной |
стены, и определяется |
следующим |
образом: при |
|
|
= 0 : |
|||||||||||||||||||||
y |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
tж (y) = tж1 |
= tв ; при y = δо : tж (y) = t ж2 |
= tн ; при x = 0 |
и 0 < y < δ: t ж (y) = tв ; |
||||||||||||||||||||||||
|
|
|
= 0 |
и δ < |
|
|
|
|
|
|
|
|
|||||||||||||||
при |
x |
y |
< (δ + δок ) : tж (y) = tср ок ; при x = 0 и (δ + δок ) < y < δо : |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
tж (y) = tн . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Коэффициент теплоотдачи α(y) является известной функцией на поверхностях оконного откоса и наружной стены; определяется следующим образом: при y = 0 : α(y) = α1 = αв ; при y = δо : α(y) = α2 = αн ;
при x = 0 и 0 < y < δ: α(y) = αв отк ; при x = 0 и δ < y < (δ + δок ) : α(y) = αок отк ; при x = 0 и (δ + δок ) < y < δо : α(y) = αн отк .
Численные значения соответствующих коэффициентов принимаются с учетом исследований К.Ф.Фокина и В.Н.Богословского для вынужденной и естественной конвекции.
Величина αн для конкретного оконного проема может определяться через значение аэродинамического коэффициента Сv, для чего находится значение скорости в расчетный период vo, а затем определяется скорость обтекания стены вблизи оконного проема v. Зная эти скорости, можно определить величину αн для условий вынужденной конвекции.
Выбрав в качестве масштаба длины толщину стены δо, а масштаба температуры – температурный напор (tж1-tж2), приведем уравнение Лапласа (1.2) и граничные условия (1.3)-(1.6) к безразмерному виду:
¶2θ |
+ |
¶2θ |
= 0 . |
(1.7) |
|
¶x 2 |
¶y2 |
||||
|
|
|
При этом x>0, 0<y<1.
Граничные условия запишутся в виде:
- |
∂θ(x,0) = Bi1 × [1 - θ(x,0)] ; |
(1.8) |
|
¶y |
|
|
8 |
|
|
- |
∂θ(x,1) = Bi |
2 × θ(x,1) |
; |
|
¶y |
|
|
∂θ(0, y) = Bi(y) × [θ(0, y) - θ |
ж (y)] ; |
||||||
¶x |
Bi1 × y + 1 |
|
|
||||
θ(¥, y) =1 - |
= F(y) . |
||||||
1 + Bi1 |
+ |
Bi1 |
|
||||
|
|
||||||
|
Bi2 |
|
|||||
|
|
|
|
||||
Здесь
(1.9)
(1.10)
(1.11)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ(x, y) = |
t(x, |
|
y) - t ж2 |
; |
|
|
|
|
(1.12) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t ж1 - t ж2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
θж (y) = |
t ж (y) - t ж2 |
; 0 £ θж (y) £1 ; |
(1.13) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t ж1 - t ж2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
α1 × δo |
|
|
α2 × δo |
|
α( |
|
|
|
|
||||||||||
x = |
|
x |
; y = |
|
y |
; Bi1 |
= |
; Bi2 |
= |
; Bi(y) = |
y) × δo |
. |
(1.14) |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
δo |
δo |
|
λ |
|
|
|
|
λ |
|
λ |
|
|||||||||||||||||
|
Таким образом, безразмерное температурное поле зависит от |
||||||||||||||||||||||||||||
следующих величин |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
θ = θ(x, y,Bi1 , Bi2 , Bi(y),θж (y)) . |
|
|
|
|
(1.15) |
||||||||||||||||
|
Будем искать решение уравнения (1.15) в виде суммы двух |
||||||||||||||||||||||||||||
функций: |
|
|
|
|
|
θ(x, y) = u(x, y) + v(x, y) . |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.16) |
|||||||||||||||
Подставим (1.16) в уравнение Лапласа (1.7) и граничные условия
(1.8)-(1.11): |
|
|
|
|
|
¶2 v + |
¶2 v = - |
¶2 u - |
¶2 u |
= 0; x > 0; 0 < y <1; |
|
¶x 2 |
¶y2 |
¶x 2 |
¶y2 |
|
|
∂v(x,0) - Bi1 × v(x,0) = - |
∂u(x,0) + Bi1 |
× u(x,0) ; |
|||
¶y |
|
|
|
¶y |
|
∂v(x,1) + Bi2 × v(x,1) = - |
∂u(x,1) - Bi2 |
× u(x,1) ; |
|||
¶y |
|
|
|
¶y |
|
∂v(0, y) - Bi(y) × v(0, y) = - |
∂u(0, y) + Bi(y) ×[u(0, y) - θ |
ж (y)]; |
¶x |
¶x |
|
v(∞, y) = −u(∞, y) + F(y) .
(1.17)
(1.18)
(1.19)
(1.20)
(1.21)
Подберем функцию u(x,y) такой, чтобы она удовлетворяла уравнению Лапласа (1.7) и доставляла функции v(x,y) на всех границах, кроме границы х=0, однородные граничные условия. Этому условию удовлетворяет функция u(x,y)=F(y). Действительно, подставив ее в (1.17)- (1.21), получим
9
¶2 v |
+ ¶2 v = 0 ; |
|
|
¶x 2 |
¶y2 |
|
|
∂v(x,0) = Bi1 |
× v(x,0) |
; |
|
¶y |
|
|
|
∂v(x,1) = -Bi2 |
× v(x,1) |
; |
|
¶y |
|
|
|
∂v(0, y) = Bi(y) ×[v(0, y) + F(y) - θ |
ж (y)] ; |
¶x |
|
v(¥, y) = 0 . |
|
(1.22)
(1.23)
(1.24)
(1.25)
(1.26)
Таким образом, неизвестная функция v(x,y) представляет собой отклонение от известного стационарного неодномерного поля температуры вдали от оконного проема. Будем искать решение задачи (1.22)-(1.26) способом Фурье. Представим искомое решение в виде произведения двух функций, одна из которых зависит только от координаты х, а другая – от координаты у
v(x, y) = X(x) × Y(y) . |
(1.27) |
Подставив (1.27) в (1.22), получим:
·· |
|
|
|
|
Y(y) |
= - |
X // (x) |
= -ε2 . |
(1.28) |
Y(y) |
|
|||
|
X(x) |
|
||
Вданном случае точки означают дифференцирование по х, штрихи
–по у; e2=const, так как левая часть равенства (1.28) зависит только от у, а правая – только от х.
Из равенства (1.28) следует
X // (x) - ε2 |
× X(x) = 0 ; |
(1.29) |
|
·· |
× Y(y) |
= 0 . |
|
Y(y) + ε2 |
(1.30) |
||
Решением (1.29) будет функция |
|
|
|
X(x) = с1 × еε×x + c2 |
× e-ε×x . |
(1.31) |
|
Решение (1.30) будет иметь вид |
|
|
|
Y(y)= с3 ×sin(ε× y)+ c4 ×cos (ε× y). |
(1.32) |
||
Подставим (1.31) и (1.32) в (1.27); получим |
|
||
v(x, y) = (c1 × еε×x + c2 × e-ε×x ) × (c3 × sin (ε × y) + c4 × cos (ε × y)) . |
(1.33) |
||
Из условия ограниченности (1.26) функции v(x,y) на бесконечности |
|||
постоянная с1=0. Тогда (1.33) перепишется в виде |
|
||
v(x, y) = (A × sin (ε × y) + B × cos (ε × y)) × e-ε×x . |
(1.34) |
||
В данном случае А и В – постоянные величины: А=с2×с3; В=с2×с4. Тем самым задача полностью решена, и безразмерное
температурное поле (1.15) имеет вид:
10
θ(x, y) =1 - Bi1 × y + 1 |
|
+ ∑ An |
×ϕn (y) × e-εn ×x |
. (1.35) |
||||
|
|
|
|
|
¥ |
|
|
|
1 + Bi1 |
+ |
Bi1 |
|
n=1 Bi1 |
|
|
||
Bi2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Анализ температурного поля (1.35) показывает, что при малых значениях безразмерной продольной координаты х от х=0 до х=х1 распределение температуры и скорости ее изменения по х в отдельных точках стены зависит от особенностей граничных условий при х=0. Математически в этой области поле температуры в стене будет определяться не только первым, но и последующими членами ряда (1.35). Эту область стены, непосредственно примыкающую к оконному проему, в которой скорость изменения температуры в направлении координаты х зависит от вида граничных условий при х=0, назовем по аналогии нестационарными температурными полями неупорядоченной областью теплопередачи через стену.
Начиная с некоторого расстояния х>х1 от оконного проема, граничные условия при х=0 начинают играть второстепенную роль, и процесс теплопередачи через стену полностью определяется только граничными условиями при у=0 и у=1, физическими свойствами материала стены и ее размерами и формой, хотя температурное поле вдоль стены и изменяется. Температурное поле в этой области х>х1 математически описывается первым членом ряда (1.35)
θ(x, y) = |
Bi1 × y + 1 |
|
+ |
A1 |
×ϕ1 (y) × e-ε1 ×x . |
(1.36) |
||
|
|
Bi1 |
|
|
||||
|
1 + Bi1 |
+ |
|
|
Bi1 |
|
||
|
Bi2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Безразмерный поток тепла, подводимый к стене на этом участке в предположении одномерного температурного поля, равен
|
|
|
|
Qo = - |
|
Bi1 × x 2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Bi |
. |
|
|
|
|
(1.37) |
|||||
|
|
|
|
|
1 + Bi1 |
+ |
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Bi2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Их отношение соответственно равно |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
(1 + Bi1 |
+ Bi1 ) × ∑ An |
/ |
(0) × (1 - e |
-εn |
×x |
) - εn |
× ∫ϕn (y) × dy] |
|||||||||
|
|
×[ϕ n |
||||||||||||||||
|
|
|
¥ |
|
|
|
|
|
|
|
2 |
|
2 |
y1 |
|
|
||
Qд =1 + |
|
|
|
εn |
|
|
|
|
|
|
|
0 |
. |
|||||
|
Bi2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
n =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Qo |
|
|
|
|
Bi12 × x 2 |
|
|
|
|
|
|
|||||||
(1.38)
Как всякая теоретическая модель, аналитическая модель, приведенная выше, отражает главные особенности рассматриваемого явления и учитывает факторы, которые в соответствии с современными представлениями являются определяющими. Некоторые стороны процесса полагаются второстепенными и могут не учитываться. Только
