
6855
.pdf60
Если в любой момент времени к движущейся материальной точке приложить силу инерции, то вместе с активной силой и реакцией связи она составит уравновешенную систему сил.
Примечание:
Фактически, применение принципа д’Аламбера означает, что задача решается в инерциальной системе отсчета связанной с точкой, а в этой системе отсчета точка является покоящимся телом.
В этом случае уравнения динамики принимают вид уравнений равновесия, из которых находятся динамические реакции связей.
На применении принципа д'Аламбера основан самостоятельный раздел динамики, который называют кинетостатикой.
Движение материальной точки по траектории
В этом случае ускорение точки(рис. 12.1) складывается из касательного и нор-
мального |
ускорений |
|
|
|
|
, поэтому сила инерции также будет пред- |
||||
|
суммы касательной< 1 |
и нормальной сил инерции: |
||||||||
ставлена в виде |
|
S S S |
|
|
|
|||||
|
|
|
|
< |
|
1 |
|
|
|
|
|
|
|
Ф Ф Ф |
|
|
Ф1 S1 n . |
||||
где |
|
Ф< S< < , |
||||||||
Движение точки вращающегося тела |
|
|||||||||
Ускорения точки вращающегося тела (рис. 12.2) называют вращательным |
||||||||||
и |
центростремительным . Им соответствуют вращательная сила инерции иS< |
|||||||||
|
|
|
|
сила1инерции: |
|
|||||
центростремительная |
< |
S |
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
Ф Ф Ф |
|
|
Ф1 S1 , 7. |
||||
где |
|
Ф< S< |
o7, |
|||||||
Сложное движение точки
При сложном движении абсолютное ускорение складывается из относительно-
го, переносного и кориолисова ускорений:
S S< S1 S/07
Им соответствуют относительная, переносная и кориолисова силы инерции: |
||||||||||
Ф |
S |
7 |
, |
Ф |
S |
|
, |
Ф |
S |
/07 |
7 |
|
|
|
|
|
/07 |
|
|||
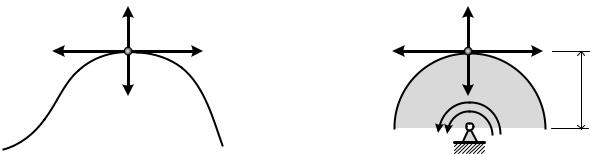
61
|
Φτ |
|
Φn |
Φτ |
|
Φn |
|
|
R |
|
R |
||
|
М |
aτ |
М |
aτ |
||
|
|
|
|
|
|
R |
|
|
|
|
|
|
an |
|
|
|
R |
|
|
r |
|
траектория |
|
an |
|
|
|
− |
|
+ |
|
ω ε |
|
|
|
|
|
|
Рис. 12.1 Рис. 12.2
12.2. ПРИНЦИП Д’АЛАМБЕРА ДЛЯ МЕХАНИЧЕСКИХ СИСТЕМ
Принцип д’Аламбера для механической системы (в записи для сил)
При движении механической системы сумма главных моментов активных сил, реакций связей и сил инерции всегда равна нулю.
Рассмотрим механическую систему, состоящую из n точек. Для каждой точки
запишем выражение принципа д'Аламбера: |
|
||||
|
|
|
|
|
(12.3) |
Ф |
S |
|
^ |
Ф , , , … , 1, |
|
─сила инерции k-й точки. |
|
||||
где |
|
|
|||
Просуммируем эти уравнения по всем точкам и получим уравнение |
|||||||
|
|
|
|
|
|
|
(12.4) |
^ Ф , |
|
|
|
|
|
|
|
в левой части которого суммируются три главных вектора: |
|||||||
|
|
|
Q |
|
|
|
|
главный вектор активных сил: |
|
Q |
|
|
|||
|
1 |
|
, |
|
|||
главный вектор реакций связей: |
|
|
|
||||
∑1 |
|
|
, |
||||
главный вектор сил инерции: |
Ф ∑Q Ф |
|
|
|
|||
^ ∑1 |
^ . |
||||||
Принцип д’Аламбера для механической системы (в записи для моментов)
При движении механической системы сумма главных векторов активных сил, реакций связей и сил инерции относительно любой точки пространства всегда равна нулю.
Выберем в пространстве произвольный центрОp и проведем из него к каждой материальной точке системы радиус вектор q.
62
Векторно умножим на него каждое слагаемое в уравнении (12.3). Получим: |
|||||||||||||
|
|
r 7 |
|
|
r 7 |
|
|
r 7 |
|
, , , … , 1, |
|||
|
|
|
|
^ |
|
|
Ф |
|
|
||||
или |
|
6 |
|
6 |
|
6 , , , … , 1. |
|||||||
|
; |
5 |
|
; |
5^ |
|
; |
5s |
|
||||
Суммируя полученные уравнения по всем материальным точкам, получим: |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
; |
|
; |
^ |
; |
s |
, |
(12.5) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
где |
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
– |
главный момент активных сил, |
|
||||||||||
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
Q |
|
|
|
− |
главный момент реакций связей, |
|
|||||||||
|
;^ |
∑1 |
; |
|
5 |
6 |
|
|
|||||||||
|
|
∑ |
Q |
|
6 |
|
|
|
|
|
|
||||||
|
; |
|
; |
|
5s |
|
|
− |
главный моментсил инерции. |
|
|||||||
|
;s |
∑1 |
; |
|
5^ |
|
6 |
|
|
||||||||
Векторные уравнения принципа д’Аламбера могут быть записаны в скалярном
виде, например в проекциях на координатные оси: |
|
|
w |
xy zy {y , |
|
|
x| z| {| , |
|
ix} z} {} , |
(12.6) |
|
|
~yx ~yz ~y{ , |
|
vi~|x ~|z ~|{ , |
|
|
t |
~}x ~}z ~}{ . |
|
Примечание:
При составлении уравнений (12.4 ÷ 12.6) внутренние силы не должны приниматься во внимание, поскольку для них главный вектор и главный момент равны нулю.
Если механическая система находится в равновесии, то силы инерции отсутствуют и уравнения принципа д’Аламбера превращаются в обычные уравнения равновесия.
12.3. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ
Чтобы при описании движения использовать принцип д’Аламбера, нужно уметь вычислять главный вектор и главный момент сил инерции.
Главный вектор сил инерции
Считая массы точек системы постоянными, преобразуем выражение для главного вектора сил инерции:

|
|
|
|
|
63 |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
• |
|
• |
|
||||||
|
|
|
||||||||
|
Ф |
Ф • |
S |
|
|
|||||
∑Q1 |
8 9 |
Q |
|
Q |
|
|
Q |
|
|
|
|
∑Q1 |
|
|
|
|
|
||||
Окончательно получаем |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(12.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
||
Главный вектор сил инерции механической системы равен производной по времени от количества движения системы, взятой с обратным знаком.
Если это соотношение подставить в (12.4), то принцип д’Аламбера примет вид теоремы об изменении количества движения:
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
, то получаем |
|
Если учесть, что количество движения системы равно |
|||||||||
|
Ф |
8 |
9 |
|
, |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Ф S |
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
(12.8) |
|
Главный вектор сил инерцииопределяется, как произведение массы системы и ускорения центра масс и направлен против этого ускорения.
Если это соотношение подставить в (12.4), то принцип д’Аламбера примет вид
теоремы о движении центра масс:
S ∑
Главный момент сил инерции
Главный момент сил инерции равен:
;Ф) ∑1Q ;) 5Ф 6 ∑ 7 r Ф ∑ 7 r S ∑ 7 r
Можно показать, что последняя сумма равна производной от кинетического момента системы, то есть:
) |
|
|
|
|
|
|
|||
; |
|
|
||
|
Ф |
-) |
|
|
|
|
|
(12.9) |
|
Главный момент сил инерции механической системы равен производной по времени от кинетического момента системы, взятой с обратным знаком.
64
В проекциях на координатные оси равенство (12.9) принимает вид:
;Ф - , ;Ф - , ;Ф - |
(12.10) |
При подстановке этого соотношения в (12.5) принцип д’Аламбера примет форму теоремы об изменении кинетического момента:
|
) |
|
|
|
|
. |
|||
∑ ; |
5 |
|||
|
6 |
|||
-) |
|
|
|
|
|
|
|
12.4. ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ ТВЕРДОГО ТЕЛА
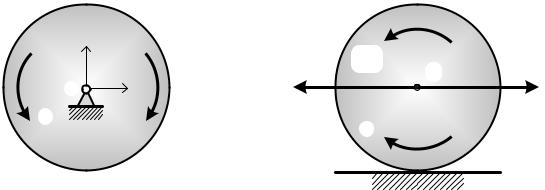
Вращение тела относительно неподвижной оси
Кинетический момент тела относительно оси вращения равен- ! o.
Подставляя эту формулу в (12.10), получим, что
главный момент сил инерции твердого тела относительно оси вращения равен по модулю произведению осевого момента инерции на угловое ускорение:
;Ф ! , ! o
(12.11)
Знак «минус» в (12.11) означает, что момент сил инерции следует направить противоположно угловому ускорению (рис. 12.3).
Если (12.11) подставить в последнее уравнение системы (12.6)
; ;^ ;s ,
то оно примет вид дифференциального уравнения вращательного движения:
! o ∑ ; 5 6.
|
|
y |
|
M Φ |
|
R |
|
|
|
|
|
||
|
|
x |
Φ |
z |
C |
aC |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
ε |
|
Φ |
|
ε |
|
|
|
|
M z |
|
|
|
Рис. 12.3 |
Рис. 12.4 |
65
Плоскопараллельное движение твердого тела
При описании плоского движения следует перейти к системе отсчета, связанной с центром масс, в которой теорема об изменении кинетического момента записывается так же, как и в неподвижной системе отсчета.
В этом случае формулы (12.9) и (12.11) сохранят свой вид:
|
|
, |
|
|
|
|
. |
; |
; |
|
! |
|
|||
|
|
|
o |
||||
Ф |
-) |
|
|
Ф |
|
|
|
|
|
|
|
|
|
||
Система сил инерции при плоскопараллельном движении будет представлена и главным вектором и главным моментом сил инерции относительно оси, проходящей через центр масс (рис. 12.4).
12.5. ПРИМЕНЕНИЕ ПРИНЦИПА Д’АЛАМБЕРА К РЕШЕНИЮ ЗАДАЧ ДИНАМИКИ
Применение принципа д’Аламбера к решению задач состоит в следующем:
К действующим на механическую систему силам следует добавить силы инерции, после чего уравнения движения можно составлять как обычные уравнения статики.
На этом подходе основан раздел динамики, называемый кинетостатикой.
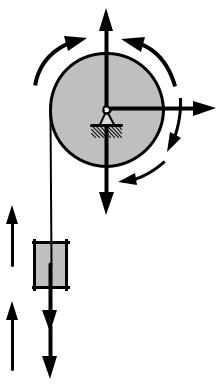
ПРИМЕР
Грузоподъемная установка состоит из барабана массойm2с осевым моментом инерцииJи радиусомr, невесомого и нерастяжимого троса и груза массойm1. К барабану приложен вращающий момент М.
Определить ускорение грузааи составляющие реакции оси барабана X0и Y0.
Решение
К телам системы приложены активные силы: сила тяжести груза@ B
исила тяжести барабана @ B.
исоставляющие реакции оси барабана: €) и •).
Добавим к ним силы инерции:
СилуS инерции груза Ф S, направив ее противоположно ускорению
за , и;пару!oс моментом, который равен главному моменту сил инерции бара-
Ф
бана o , направив эту пару противоположно угловому ускорению барабана .
|
66 |
|
|
R |
|
|
Y0 |
|
M |
M zΦ |
|
|
R |
|
|
X 0 |
|
|
ε |
|
|
ω |
|
R |
R |
|
G2 |
||
v |
||
|
R |
|
R |
G1 |
|
a |
|
|
|
R |
|
|
Φ |
|
|
Рис. 12.5 |
При таком направлении сил инерции знаки окажутся учтенными, и далее надо |
|
будет оперировать только с модулями этих величин: |
Ф S и ‚;Ф‚ !o. |
Теперь, в соответствии с принципом д'Аламбера, уравнения движения можно составлять как обычные уравнения статики для данной плоской системы сил:
w |
• |
|
|
|
|
€ |
||||
|
|
|
|
|
|
|
||||
u |
• |
|
|
|
||||||
v |
|
|
|
|
|
|
|
|
• @ |
@ Ф |
) |
|
|
идалее i; ‚;Ф‚ @ 7 Ф7 . |
|||||||
t• ; |
6 |
|
|
|
|
|||||
|
5 |
|
|
|
|
|
||||
u |
|
|
|
|
|
|
|
|
|
|
Теперь подставим в эти уравнения выражения сил инерции: |
||||||||||
|
Ф S |
и |
‚;Ф‚ !o, |
|
|
|||||
выражения сил тяжести: |
|
|
и |
|
|
|
||||
|
|
|
|
, |
|
|||||
|
@ |
|
B |
|
@ |
B |
|
|
||
и учтем, что |
S o7. |
|
|
|
|
|
||||

€ 67
i• B B S ; ! S7 B 7 S 7 .
Решая систему уравнений, получим величину ускорения:
ST; 7 BU‡T ! 7 U,
ивертикальную и€горизонтальную• составляющиеB B реакцииS оси барабана:
, .
Тема 13.
Уравнения Лагранжа второго рода
13.1. ПРИНЦИП Д’АЛАМБЕРА – ЛАГРАНЖА
Принцип д’Аламбера ─ Лагранжа объединяет в себе принцип д’Аламбера и принцип Лагранжа.
Рассмотрим механическую систему из nматериальных точек, на которую наложеныmидеальных голономных стационарных удерживающих связей.
Для каждой точки запишем выражение принципа д’Аламбера: |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
^ |
|
Ф , , , … , 1. |
|||||||||||||||
Придадим точкам системы возможные перемещения |
|
|
. Каждое из приведен- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
возможное перемещение и про- |
||||
ных уравнений умножим на соответствующее |
|
|
b7 |
|
||||||||||||||||||||
суммируем уравнения: |
|
|
|
|
|
Q |
|
|
|
|
Q |
|
|
|
||||||||||
|
∑ |
Q |
|
b7 |
|
∑ |
b7 |
∑ |
. |
|||||||||||||||
|
1 |
|
|
1 |
|
|
^ |
|
1 |
Ф |
b7 |
|
||||||||||||
|
∑ |
^ |
b7 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Учтем, что |
|
|
|
|
|
|
|
|
поскольку все связи идеальны. |
|||||||||||||||
Получим уравнение, которые называют общим уравнением динамики: |
||||||||||||||||||||||||
|
∑ |
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
5 |
|
Ф |
6 b7 |
|
|
|
|
|
|
|
|
|
(13.1) |
|||||||||
или |
∑ |
Q |
|
S |
|
6 b7 |
|
. |
|
|
|
|
|
|
|
|||||||||
1 |
5 |
|
|
|
|
|
|
|
|
|
(13.2) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
68
Принцип д’Аламбера ─ Лагранжа
При движении механической системы сумма возможных работ активных сил и сил инерции на любых возможных перемещениях равна нулю.
Если система находится в равновесии и силы инерции отсутствуют, то уравнения (13.1) принимают вид общего уравнения статики (11.1):
1 b7 .
•Q
Таким образом, принцип возможных перемещений Лагранжа является частным случаем принципа д’Аламбера ─ Лагранжа.
Если в уравнении (13.1) вариации координат выразить через вариации обобщенных координат, используя для этого формулу (10.4):
b7 ∑hQ2 W7Wfh bfh, |
k=1, 2, …, n, |
|
|
|
|
|||||||||
получим следующее соотношение: |
|
|
|
|
|
|
|
|
|
|||||
∑ |
hQ |
Z∑ |
Q |
|
Wfh |
∑ |
Q |
|
[ bf |
h |
|
|
||
|
|
|
|
s Wfh |
|
, |
||||||||
|
2 |
|
1 |
|
W7 |
|
|
1 |
|
W7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в котором первое слагаемое в скобкеявляется обобщенной силой, соответству- |
|||||
ющей j-й обобщенной координате: |
|||||
|
h |
∑ |
Q |
Wfh |
|
|
|
|
|||
|
|
|
1 |
|
W7 , |
|
|
|
|
|
|
а второе слагаемое, равное |
|
||
|
|
∑ s Wfh |
|
|
s |
1 |
W7 |
|
h |
Q |
|
назовем обобщенной силой инерции для
(13.3)
j-й обобщенной координаты.
При этих обозначениях уравнение принципа д’Аламбера-Лагранжа примет вид: |
|
∑hQ2 5h hs6 bfh , h , , … , 2. |
(13.4) |
Поскольку обобщенные координаты не зависят друг от друга, каждую из них можно менять, не меняя при этом остальных.
Зафиксировав все обобщенные координаты, кроме одной fh, получимуравнение
h s
h .
69
Общее число уравнений, которые таким образом можно сформировать, равно s. Вместе они представляют выражение принципад’Аламбера-Лагранжа в обоб-
щенных силах: h hs , h , , … , 2. |
(13.5) |
Принцип д’Аламбера ─ Лагранжа в обобщенных силах
При движении механической системы сумма обобщенной активной силы и обобщенной силы инерции по каждой обобщенной координате равна нулю.
Примечание:
Если система находится в равновесии, то силы инерции отсутствуют и уравне-
ние (13.5) приобретает, h , , …вид, 2принципа Лагранжа в обобщенных силах (11.2):
h .
То есть, принцип Лагранжа является частным случаем принципа д’АламбераЛагранжа.
13.2. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
Лагранжем были предложены две формулировки уравнений для описания движения механических систем. Уравнения Лагранжа первого рода мы не рассматриваем, поскольку они не получили широкого распространения.
Уравнения Лагранжа второго рода, наоборот, получили широчайшее применение, поскольку обладают целым рядом достоинств:
Число этих уравнений минимально и равно числу степеней свободы s; Они не содержат реакций идеальных связей; Они находят применение не только в механике, но и в других науках.
Для формулировки этих уравнений Лагранж и Эйлер выразили обобщенные силы инерции через кинетическую энергию системы, получив выражение:
|
|
Z Wfg Wf [ , |
h , , … , 2 |
. |
|
|
s |
WI |
WI |
|
|
|
h |
h |
h |
|
|
|
|
|
|
||
После подстановки этих уравнений в уравнения принципа Лагранжа-
Даламбера (13.5), получаем уравнения, которые называют
