6848

70

Решение:

Применим теорему об изменении главного вектора количества движения систе-

Если обозначить количество движения системы в начальный момент времени как

3.4 Теорема об изменении кинетической энергии в интегральной форме

Изменение кинетической энергии механической системы за некоторый промежу-

ток времени равно сумме работ всех действующих в системе сил:

¸ ¸§ ∑?±KD ¹±

или, выделяя отдельно работы внешних и внутренних сил:

71

При вращении тела относительно некоторой оси z его кинетическая энергия рав-

на: ¸ D ½•~ .

При плоскопараллельное движение тела кинетическая энергия равна:

¸пл D ©)” D ½•”~ ,

где )” скорость центра массы тела, а ½•” момент инерции тела относительно оси, проходящей через центр массы тела перпендикулярно оси вращения.

Работа силы на конечном перемещении определяется как криволинейный инте-

Работа постоянной силы на прямолинейном перемещении равна произведению модуля силы на модуль перемещения и на косинус угла между направлением силы и перемещением: А12 (F ) = F cos α × S.

Рис. 3.7

При этом: A (F) > 0, если 0 < α < π/2, A (F) = 0, если α = π/2,

A (F) < 0, если π/2 < α < π.

72

Моментом инерции материальной точки относительно некоторой оси (осевым моментом инерции) называется величина, равная произведению массы точки на квадрат ее расстояния до этой оси: Jz = m h2 .

Моменты инерции некоторых однородных тел:

1.Тонкий прямолинейный однородный стержень массой М и длиной l:

Jz= (Ml2)/12.

2.Тонкая прямоугольная пластинка массой M и размерами a × b:

Jx = (M/12)(a2 + b2).

3.Тонкое однородное кольцо массой M и радиусом R: Jс = MR2 .

4.Тонкая круглая пластинка (однородный диск) массой M и радиусом R:

Jс = MR2/2 .

При решении задач приходится вычислять моменты инерции тел относительно осей вращения, которые не проходят через центр масс.В этом случае применяют

теорему Гюйгенса – Штайнера:

Момент инерции механической системы (тела) относительно некоторой оси равен сумме момента инерции относительно параллельной ей оси, проходящей через центр масс, и величины равной произведению массы системы на квадрат расстояния между осями: J z = J zC + md 2

Задача 3.9. Кинетическая энергия

Ступенчатое колесо радиуса , масса которого m равномерно распределена по окружности радиуса ", катится по прямолинейному горизонтальному рельсу без проскальзывания, касаясь рельса ободом радиуса 2", имея в точке С скорость )̅. Чему равна кинетическая энергия тела?

Решение:

73

Так как колесо совершает плоскопараллельное движение, то его кинетическая энергия вычисляется по формуле:

стержню, проходящему через центр С, вращается относительно оси, проходящей через точку О, лежащую на ободе, перпендикулярно плоскости диска, имея в т. С скорость ).

определить момент инерции относительно оси вращения, проходящей через точку

О: ½Â ½” © ∙ ÿ DO © © NO © .

74

Зная эту величину, можно определить кинетическую энергия диска:

¸ D ∙ NO © ∙ ~ O © ~ .

При вращательном движении угловая скорость находится по формуле

~ )⁄ÿ )⁄ .

Тогда кинетическую энергию диска можно выразить через его массу и скорость

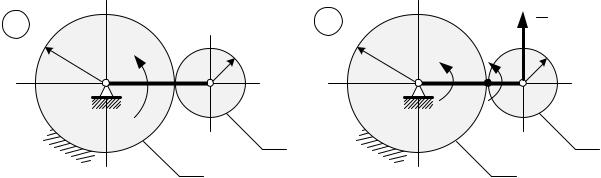
Задача 3.11. Кинетическая энергия В планетарном механизме с внешним зацеплением водило ОА, вращающееся во-

круг неподвижной оси О с угловой скоростью ~, приводит в движение зубчатое колесо массой ©, катящееся по неподвижному колесу 2. Если колесо 1 – однородный диск, то чему равна его кинетическая энергия?

Рис.3.10

Решение:

Колесо 1 совершает плоскопараллельное движение и его кинетическая энергия равна: ¸ D ©)А D ½А~D,

Так как колесо 2 неподвижно, то точка Р является мгновенным центром скоро-

В этом случае угловую скорость колеса 1 можно определить по формуле:

~D ) ⁄¹ ~$ D &⁄ D.

Подставляя все в формулу кинетической энергии, получим:

75

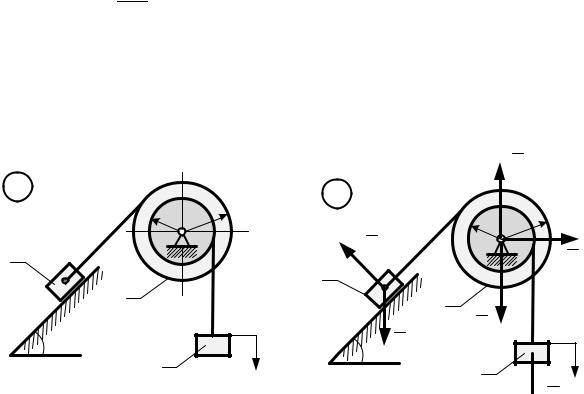
Задача 3.12. Теорема об изменении кинетической энергии Система состоит из тел 1, 2 и 3, связанных между собой посредством нерастяжи-

мых нитей. Проскальзывание нерастяжимых нитей отсутствует, силой трения пренебрегаем. Блок 2 состоит из двух ступеней разных радиусов 1.5", массы всех тел одинаковы и равны © 3 кг, угол Ä 30§. Движение начинается из положения покоя и при перемещении груза на величину Å $м& система имеет кинетическую

энергию ¸ 1.8¶ Œкг∙м1•.

с1

Найти величину перемещения Å.

Решение:

Применим теорему об изменении кинетической энергии системы:

¸D ¸§ ∑?±KD ¹´± ∑?±KD ¹º±

P1

Рис.3.11

Начальная кинетическая энергия равна нулю, то есть ¸§ 0, так как в начальный момент времени система неподвижна. Сумма работ внутренних сил равна нулю, так

Вычислим работу внешних сил.

К внешним силам относятся: силы тяжести: D, ′D, , реакция плоскости µ, ре-

акции шарнира О: Â, Â.

¹»µ¼ ¹» ¼ ¹» ¼ ¹» ¼ 0,

76

¹» D¼ D ∙ Å ©¶Å 3¶Å,

¹ Œ ′D• ′D ∙ Å ∙ " ∙ ;F7 30§ ©¶Å ∙ " ∙ ;F7 30§ ©¶Å ∙ 32 ∙ 12 2.25¶Å.

Составим уравнение ¸D ∑?±KD ¹´±:

1.8¶ 3¶Å 2.25¶Å, 1.8¶ 0.75¶Å,

Откуда получаем, что Å §D.ÇÁÆ.ÀÆ 2.4$м&. Ответ: Å = 2.4 м.

3.5 Принцип возможных перемещений

Для того чтобы механическая система находилась в равновесии, необходимо и достаточно, чтобы возможная работа всех активных сил на любых возможных пе-

Возможными перемещениями точки называются воображаемые бесконечно малые перемещения точки системы, допускаемые в каждый момент времени наложенными на нее связями.

Правила определения работы силы и момента показаны на рисунке 3.12.

Рис.3.12

Задача 3.13. Принцип возможных перемещений Определить реакции опор балки(рис.3.13,а).

Решение:

Заданная составная балка образована из четырех элементарных балок, соединенных шарнирами F, G и H, и загружена системой параллельных сил.

77

Распределенную нагрузку, приложенную к каждой из элементарных балок, заменяем равнодействующими Q1 и Q2 соответственно.

1. Для определения вертикальной составляющей в неподвижной опоре A отбросим вертикальную линейную связь, заменив ее искомой реакций YA = RA , сообщим точке A возможное перемещение δsA = AA´и построим соответствующую моду бал-

ки (рис. 3.13, б).

Уравнение для определения RА:

RА δsА + Q2δsQ2 – P 1δsG – M 1δφD – M 2δφE + P2δsP2 = 0.

Выразим все возможные – линейные и угловые перемещения точек системы через

δφE:

δsP2 = a δφE;

δφD = 2 δφE, поскольку δsH = a δφD = 2a δφE; δsG = δsH = 2a δφE;

δsQ2 = δsG = 2a δφE;

δsА = δsF = 2δsQ2 = 4a δφE.

Получаем:

(4RА + 2Q2 – 2P 1 – 2M 1/а – M 2/а + P2 ) a δφE = 0,

откуда

RА = (1/4)( – 2Q 2 + 2P1 + 2M1/а + M2/а –P 2 ) = (1/4)(– 2P + 2P + 2P + P – P) = P/2 .

79

Уравнение ПВП для определения RB:

(RB – Q 1) δsB – Q 2 δsQ2 + P1 δsG + M1 δφD + M2 δφE – P 2 δsP = 0.

Выражаем все возможные – линейные и угловые перемещения точек системы через δφE:

δsP2 = a δφE;

δφD = 2 δφE, поскольку δsH = a δφD = 2a δφE; δsG = δsH = 2a δφE;

δsQ2 = δsG = 2a δφE;

δsB = (1/2)δsF = δsQ2 = 2a δφE.

Получаем: (2RB – 2Q 1 – 2Q 2 + 2P1 + 2M1/а + M2/а – P 2 ) a δφE = 0,

откуда

RB =(1/2)(2Q1 2Q2 –2P 1 –2M 1/а –M 2/а +P2)=(1/2)(2P +2P –2P –2P –P +P)= 0 .

3. Чтобы найти RС отбрасываем подвижную опору С, заменяя ее неизвестной реакцией, сообщаем этой точке возможное перемещение δsС= CC´и строим соответствующую моду балки (рис. 3.13, г).

Соответствующее уравнение ПВП примет вид:

– Q 2 δsQ2 + RС δsС – P 1 δsG – M 1 δφD – M 2 δφE + P2 δsP = 0.

Выражаем все возможные – линейные и угловые перемещения точек системы через δφF:

δsQ2 = a δφF; δsС = 2a δφF; δsG = 3a δφF;

δφD = 3 δφF, поскольку δsG= a δφD = 3a δφF;

δφE = (1/2)δφD = (3/2) δφF, поскольку δsH = a δφD = 2a δφE; δsP = a δφE = (3/2)aδφF.

Получаем: [–Q 2 + 2RС – 3P 1 –(3/a)M 1 –(3/2a)M 2 +(3/2) P2] a δφF=0, откуда RС=(1/2)(Q2+3P1+(3/a)M1+(3/2a)M2–(3/2)P 2)=

=(1/2[P+3P+3P+(3/2)P–(3/2)P]=(7/2)P .

4. Для определения RD отбрасываем подвижную опору в точке D, заменяя ее неизвестной реакцией, сообщаем этой точке возможное перемещение δsD = DD´и строим соответствующую моду балки (рис. 3.13, д).

Уравнение ПВП для определения RD:

RD δsD + M1 δφG + M2 δφE – P 2 δsP2 = 0.

Выражаем все возможные – линейные и угловые перемещения точек системы че-

рез δφE: δsD = δsP2 = aδφE ;

δφG = δφE , поскольку δsH = 2a δφD = 2a δφE.