4.6. Оценка качества уравнений регрессии

Основной показатель качества представления экспериментальных данных уравнениями регрессии – величина стандартной ошибки, вычисляемой по формуле:

. (4.26)

где:

y_i - экспериментальное значение результативного показателя

эффективности в i – ом варианте экспериментального исследования;

–значение результативного показателя эффективности в

i – ом варианте, вычисленное по аппроксимирующей зависимости;

n – количество вариантов экспериментального исследования;

–количество коэффициентов при переменных;

к – количество изменяемых факторов.

Кроме этого показателя рекомендуется использовать дополнительные показатели, вводимые на основе дисперсионного анализа. Отметим, что если показатель (4.26) не накладывает никаких ограничений на переменные, по которым производится аппроксимация, то дисперсионный анализ требует, чтобы переменные, по которым производится аппроксимация подчинялись бы нормальному закону. Дисперсионный анализ основан на разложении общей изменчивости результативного показателя (общей дисперсии) на объяснённую дисперсию, которую удалось объяснить изменением переменных, вошедших в уравнение регрессии, и остаточную регрессию, которую объяснить не удалось. Для проведения дисперсионного анализа вычисляются.

1. Объяснённая сумма квадратов:

(4.27)

с количеством степеней свободы:

среднее значение суммы квадратов:

(4.28)

2. Остаточная сумма квадратов:

(4.29)

с количеством степеней свободы:

среднее значение суммы квадратов:

(4.30)

3. Общая сумма квадратов:

(4.31)

с количеством степеней свободы:

Должно выполняться равенство:

4. Критерий Фишера

(4.32)

с количеством степеней свободы:

5. Коэффициент множественной детерминации, который показывает, какую часть изменения результативного показателя удалось объяснить изменением переменных, вошедших в уравнение регрессии.

(4.33)

с количеством степеней свободы:

По статистическим таблицам для критерия Фишера и коэффициента множественной детерминации с вышеприведёнными количествами степеней свободы и рекомендуемого уровня значимости 0.05 находят их критические значения. Если вычисленные значения критерия Фишера и коэффициента множественной детерминации не меньше критических значений, то результаты аппроксимации признаются удовлетворительными.

6. Ввиду того, что коэффициенты уравнения регрессии вычисляются по случайным величинам, то они и сами являются случайными величинами. Поэтому можно вычислить их стандартные ошибки и по ним определить критерий Стьюдента и уровни их значимости.

(4.34)

где

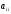- диагональный элемент матрицы

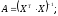
(4.35)

чем больше величина , тем лучше.

По статистическим таблицам для вычисленных значений , длястепеней свободы, для рекомендованного уровня значимостинаходим критическое значение критерия Стьюдента. Если вычисленные значенияпревышают критическое, то считаем, что уровень значимости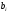не превышает рекомендуемого значения, и поэтому вычисленные значения коэффициентов приемлемы для отображения экспериментальных данных. В противном случае рекомендуется подобрать другие, сравнительно несложные функции от переменных для ввода их в аппроксимирующее уравнение регрессии.

3. Выбор решения

По построенной математической модели, представляющей собой совокупность уравнений регрессии, которые позволяют вычислять результативные показатели эффективности объекта экспериментального исследования (отклики) по задаваемым значениям факторов, можно оценить степень влияния факторов на отклики и на основании такой оценки принять инженерное решение по изменению факторов.

Для оценки степени влияния факторов на отклики можно использовать

удельные веса факторов и коэффициенты эластичности. Коэффициенты эластичности показывают на сколько процентов изменится отклик при изменении конкретного фактора на один процент. Если в уравнения регрессии не входят произведения факторов между собой, то удельные веса и коэффициенты эластичности можно вычислить для состояния экспериментального объекта, ограниченного заданными диапазонами изменения факторов. При наличии в уравнениях регрессии произведений факторов между собой удельные веса и коэффициенты эластичности вычисляются для какого-нибудь одного состояния, например, для средних или последних значений всех факторов.

Изменение j – го отклика экспериментального объекта, вносимое i – м фактором определяется по формуле

. (4.36)

, ,

где – значениеj – й функции при максимальном значении i – го фактора, влияние свободного члена уравнения регрессии, кроме i – го не учитывается;

–значение j – й функции при минимальном значении i – го фактора, влияние свободного члена уравнения регрессии, кроме i – го не учитывается.

Коэффициент эластичности i – го фактора в j – м результативном показателе вычислим по формуле:

, . (4.37)

Удельный вес i – го фактора в изменении j – го результативного показателя вычислим по формуле:

, . (4.38)

Коэффициент эластичности показывает, на сколько процентов изменится j – й результативный показатель при изменении i – го фактора на один процент. В качественном плане знак плюс говорит о положительном влиянии фактора, то есть увеличение фактора приводит к увеличению результативного показателя, а знак минус указывает на отрицательное влияние фактора, то есть при увеличении фактора уменьшается результативный показатель. Как правило для удобства в принятии инженерного решения вычисленные значения удельных весов представляются круговыми диаграммами, а коэффициенты - эластичности столбчатыми диаграммами. Если же возникают затруднения в принятии инженерных решений, то рекомендуется применение методов оптимизации. Подчеркнём. что построение математической модели не конечная цель экспериментального исследования а главным образом – инструмент для генерации инженерного решения, направленного на повышение эффективности функционирования экспериментального объекта.

Постановка задачи оптимизации в общем случае сводится к максимиза-

ции или минимизации целевой функции с ограничнеиями на остальные функции и оптимизируемые факторы:

(4.30)

.

.

.

.

Наиболее простой случай, когда нет никаких ограничений. В этом случае применяется классический метод вычисления экстремального значения по решению системы в частных производных по оптимизируемым переменным.

(4.31)

Необходимым условием экстремального значения является равенство нулю частных производных. Экстремальное значение находится решением системы уравнений в частных производных.

Рассмотрим двухфакторную математическую зависимость:

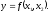
Вид экстремума определяется значением вторых частных производных:

(4.32)

1. Если и, то имеем максимум.

2. Если и, то имеем минимум.

3. Если то «седло», т. е. нет ни минимума, ни максимума.

4. Если , то экстремум может быть или не быть. Требуется дополнительное исследование.

Найдём экстремальное значение для двухфакторной зависимости:

(4.33)

Проведём вычисление первых частных производных, значений аргументов в экстремальной точке и вторых частных производных:

(4.34)

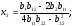
В случае невозможности отказа от ограничений на функции и оптимизируемые факторы рекомендуется использовать стандартные процедуры оптимизации, например, процедуры линейного программирования, в ППП EXCEL 2007, если все функции в постановке задачи (4.30) линейны. Если же функции нелинейные, то рекомендуется использовать процедуру ППП EXCEL 2007. реализующую метод Ньютона (касательных). Единственное ограничение данного метода – требование чтобы оптимизируемая целевая функция была дважды дифференцируема.