Глава 3. Общие методы оптимизации

3.1. Классификация методов получения оптимальных решений

Предполагая, что подлежащая оптимизации задача некоторым образом определена (не обязательно математически), общие методы оптимизации можно классифицировать следующим образом:

1. Аналитические методы, использующие классические методы дифференциального и вариационного исчисления. Эти методы заключаются в определении экстремумов функции f(х) путем нахождения тех значений x = х^*, которые обращают в нуль производные f(х) по x (рис 8).

f(х)

х

х^*₁ х^*₂

Рис. 8

В случае поиска экстремума функции f(х) при наличии ограничений применяются такие методы, как метод множителей Лагранжа и метод ограниченных вариаций. При использовании аналитических методов задача оптимизации должна быть сформулирована математически так, чтобы можно было обращаться со всеми фигурирующими в ней функциями и переменными при помощи известных правил. Для решения больших и существенно нелинейных задач аналитические методы часто оказываются непригодными, и поэтому в данном курсе они не рассматриваются.

2. Численные методы, использующие предшествующую информацию для построения улучшенных решений задачи при помощи итерационных процедур (последовательных приближений). Численные методы применяются для решения задач, которые не могут быть решены аналитически.

Поскольку большинство практических задач поддаются решению численными методами, эти методы нелинейного программирования изучаются в данном курсе.

3. Графические методы. Они основаны на графическом изображении функции в зависимости от одной или нескольких переменных. Экстремум функции в этом случае определяют непосредственно путем анализа ее графика. Преимущество графических методов заключается в их простоте. Однако, они применимы лишь тогда, когда критерий качества является функцией одной или максимум двух независимых переменных.

В экономическом моделировании в графическом виде задаются, например, функции спроса и предложения, функции потребления и линии бюджетных ограничений, зависимости величины спроса от дохода

4. Экспериментальные методы, при которых экстремум находится путем непосредственного экспериментирования с реальным объектом.

5. Методы исследования различных вариантов (например широко распространенный на практике так называемый метод проб). Эти методы основаны на анализе нескольких возможных решений одной и той же задачи с целью выбора наилучшего. Очевидно, что «наилучшее» решение, полученное этими методами, будет скорее всего лишь субоптимальным.

3.2. Оптимальные решения

Необходимые понятия и определения.Множеством(чаще говорят –линией)уровняq(q– число, в экономических приложенияхq≥ 0) функции называется множество (совокупность) всех пар(х₁ , х₂) такое, чтоf (х₁, х₂) =q, т.е. во всех точках(х₁ , х₂), принадлежащих множеству уровняq, частное значение функции y = f (х₁ , х₂) одно и то же и равноq. На рис. 9 наглядно иллюстрируется это важное математическое понятие.

Y

X₁

Глобальный оптимум

X₂

Локальный оптимум

Седловая точка

Рис. 9

Множество всех линий равного уровня называется картой линий уровня функции y = f (х₁ , х₂). По карте можно получить довольно точное представление о характере функции f (х₁ , х₂).

Точки минимума и максимума называются точками экстремума, а значения функции в этих точках называются экстремумами функции. При поиске оптимальных решений, различают понятия мультимодальных (многоэкстремальных) и унимодальных (содержащих один единственный экстремум) функций.

f (х)

f (х)

х

х

Унимодальная функция

Мультимодальная функция

Рис. 10

Соответствующий экстремуму вектор х^* = [х^*₁, . . . х^*_n]^Т называется оптимальной точкой, а соответствующее значение f (х^*) — оптимальным значением целевой функции f (х) (рис.8). Пара х^* и f (х^*) составляют оптимальное решение.

На рис. 10 показано, что если целевая функция у = f (х) является мультимодальной, то у нее могут существовать различные типы оптимальных решений f (х^*).

Глобальное оптимальное решение представляет собой наименьшее (наибольшее) значение f (х), тогда как локальное (относительное) оптимальное решение представляет собой наименьшее (наибольшее) значениеf (х) в окрестности некоторого векторах. Как для глобального, так и для локального минимума

f (х^*) ≤ f (х),

но для глобального оптимального решения это соотношение выполняется для всех х, тогда как для локального оптимального решения это имеет место только для малой области искомого решения.

Необходимое условие экстремума.Отметим, что условие экстремума функцииy = f (х₁ , х₂)

∂f (х₁ , х₂)

∂х₁

∂f (х₁ , х₂)

∂х₂

= 0,

= 0,

является необходимым, но недостаточным, так как в особой точке, которая называется «седловой», эти условия так же выполняются, хотя она и не является точкой экстремума (см. рис. 9).

Все алгоритмы поиска экстремума функций дают лишь локально оптимальные решения, так как на каждом этапе решения при движении к х^* они зависят в основном от локальных свойств целевой функции и ограничений. Правда, некоторые алгоритмы вероятнее всего заканчиваются в точке глобального оптимума, так как при поиске рассматривается широкий диапазон изменениях, однако сходимость к глобальному оптимуму не может быть гарантирована без дополнительных сведений относительно природы целевой функции и ограничений.

К счастью, для задач, соответствующих экономическим процессам, целевая функция обычно является унимодальной и обладает единственным экстремумом. Поэтому для большинства практических целей использование численных процедур, дающих локальное решение задачи оптимизации, не является большим недостатком.

Выпуклые и невыпуклые области. Понятия выпуклости и невыпуклости полезны при определении того, при каких условиях локальное оптимальное решение является также глобальным. Требование унимодальности функции является значительно более слабым, чем требование вогнутости или выпуклости, поскольку, как видно из рис. 10, унимодальность не требует непрерывности и единственности производной.

Область (множество) называется выпуклой в рассматриваемом пространстве, если для всех пар точекх₁ их₂, принадлежащих этой области, отрезок прямой линии, соединяющей их, также полностью принадлежит этой области. На рис 11 изображены выпуклаяDи невыпуклаяGобласти в двумерном пространстве.

х₂

х₂

G

D

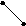
х₁

х₁

Рис. 11

Наглядно понятие выпуклого множества можно пояснить так: выпуклое множество – это область, которая не имеет вмятин и дыр. На рис 11 представлено невыпуклое множество G, которое имеет одну вмятину и одну дыру.