5.4. Методы минимизации без ограничений, использующие производные

Общая задача нелинейного программирования без ограничений сводится к следующей:

минимизировать

где является целевой функцией. При решении этой задачи мы используем методы минимизации, которые приводят к стационарной точке, определяемой уравнениемгде- градиент функции.

Градиент функции. Множество точек, для которых целевая функция имеет постоянное значение, называетсялинией уровняфункцииf(x).Несколько таких линий уровня изображено на рис.9. Если целевая функция непрерывна и дифференцируема, то существуетградиентf(x), определяемый как вектор-столбец из первых частных производныхf(x) пох, значения которых берутся в данной точкеx^(k). Верхний индексk, k= 0,1,..., используется для обозначения точки в пространстве Е^п,в которой берется значение градиента.

Градиент в точке х^(k) равен

(5.4.1)

Таким образом, градиент функции n – переменных естьn – мерный вектор и обозначается символомили. Градиент скалярной функции направлен в сторону наискорейшего увеличения функции, т.е.наискорейшего подъема,и он ортогонален линии уровняf(x),проходящей через данную точкуx^(k). Вектор, противоположный градиенту (отрицательный градиент), направлен в сторонунаискорейшего спуска.

Пример 5.4.Для функциидвух переменныхх₁их₂

а) построить линию уровня проходящую через точку ;

б) найти градиент функции в этой точке (4, 1);

в) построить этот градиент.

Р е ш е н и е з а д а ч и.

а) Сначала найдем уровень q⁰,который равен частному значению функциив точке (4, 1).

Имеем:Построим на плоскости Ох₁х₂линию, уравнение которой имеет вид:, илиилиили, наконец,(рис.18).

(2;2)1)

х₂

(4,25; 2)

2

4

grad y(4;1)

(0,25; 1)

1

1

L₂

(4;1)

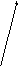
К

grad y(4;1)

0

х₁

2

Рис.18

б) Имеем:

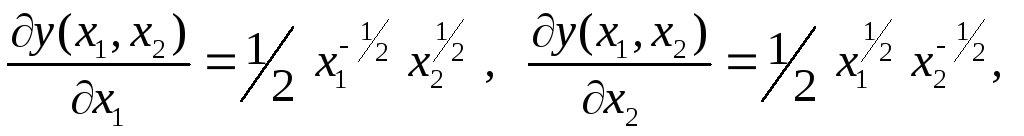
Следовательно,

в) Строим градиент на плоскости Ох₁х₂, сначала выходящим из точки (0, 0), а затем из точки (4, 1) (см. рис. 18). Следует обратить внимание, что на рис.18 градиент перпендикулярен (ортогонален) касательнойК к линии равного уровня (гиперболе)в точке (4, 1). Это есть иллюстрация общего факта: градиент в точкевсегда ортогонален линииуровняq⁰, проходящей через точку.

Метод наискорейшего спуска (метод Коши). Применение данного метода для решения задачи минимизации без ограничений было рассмотрено еще известным французским математиком Коши. Как уже отмечалось, градиент целевой функции f(x) в любой точке х есть вектор в направлении наибольшего локального увеличения f(x). Следовательно, при минимизации нужно двигаться в направлении, противоположном градиенту f(x), т.е. в направлении наискорейшего спуска, Введение направления, противоположного нормированному (единичному) градиенту f(x), т.е. направления наискорейшего спуска, определяемого в точке х^(k) по формуле

(5.4.2)

дает следующую формулу перехода из х^(k) в х^(k+1) :

(5.4.2)

где: - единичный вектор в направлении;

λ^(k) – скаляр, определяемый соотношением= λ^(k) .

Отрицательный градиент дает только направление оптимизации, но не величину шага. При этом можно использовать различные процедуры метода наискорейшего спускав зависимости от выбора λ и определения выражения . Поскольку один шаг в направлении наискорейшего спуска в общем случае не приводит в точку минимумаf(x), формула (6.4.2) должна применяться несколько раз, до тех пор, пока минимум не будет достигнут. В точке минимума все составляющие вектора градиента равны нулю.

При этом процедура наискорейшего спуска может закончиться в стационарной точке различного типа. Обычно бывает необходимо определить, является ли данная точка точкой локального минимума (т.е. решением) или седловой точкой. Если это седловая точка, то следует применить какой-либо неградиентный метод, чтобы выйти из нее, после чего минимизация может продолжаться как и ранее. В качестве критерия окончания последовательной процедуры при движении в направлении наискорейшего спуска применяются различные правила, основанные либо на значении f(x) и величинах х, либо на некоторой их комбинации, а также на соответствующих значениях этих величин на предыдущих шагах. Успех того или иного метода в смысле эффективности сходимости к локальному минимуму зависит от этих правил, а также и от самой задачи.

При выборе размера шага применяются различные способы, в простейшем из которых величина λ выбирается фиксированной или меняется от шага к шагу. Значение множителя λ должно тщательно контролироваться во избежание как неожиданного роста f(x), так и чрезмерного числа шагов, необходимого для достижения решения. Первое произойдет, если λ слишком велико, а второе, если λ очень мало или если λ настолько велико, что приводит к колебаниям около точки минимума. Таким образом, величина λ должна уменьшаться при приближении к точке минимума, для чего в алгоритм минимизации можно ввести некоторый критерий для вычисления λ на каждом шаге итерационного процесса.

Пример 5.5. В этом примере описываются несколько циклов метода наискорейшего спуска с целью иллюстрации методики решения задач минимизации.

Рассмотрим задачу минимизации целевой функции

Возьмем сначала фиксированную длину шага λ, начальное значение которой равно единице. На каждом этапе нам понадобятся значения следующих функций:

Начиная с точки х⁽⁰⁾ =поиск минимума осуществляем следующими этапами (табл. 5):

Т а б л и ц а 5

Этап	х1	х2				Величина шага при переходе к следующему этапу
0 1 2 3	2 1,96 1,88 0,88	2 1,00 0 0	4 3,92 3,76	100 50 0	≈100 50,1 3,76	-0,04 -0,078 -1,00	-1,00 -1,00 0

Для того, чтобы метод сходился, λ обычно надо уменьшать, иначе при подходе к минимуму возникнут колебания («вперед-назад»). Заметим, что в точке минимума х =

Если нелинейная целевая функция слишком сложна чтобы ее можно было продифференцировать аналитически, то составляющие градиента, являющиеся частными производными по оптимизируемым переменным, аппроксимируются разностными соотношениями.

Основной трудностью при использовании метода наискорейшего спуска, является его зависимость от выбора масштаба оптимизируемых переменных, который приходится вводить при минимизации функций с большим разбросом коэффициентов по величине («жесткие задачи»). Такие уравнения часто встречаются у сильно вытянутых и сплюснутых гиперповерхностей, образующих «хребет» или «овраг». Для таких функций процедура наискорейшего спуска сходится слишком медленно, чтобы быть эффективной, или вообще может не сойтись за разумное время. Одним из выходов в этой ситуации является использование информации по производным второго порядка. Другим подходом является масштабирование независимых переменных в целевой функции.