Применение производственных функций для экономического анализа. Рассмотрим несколько примеров построения целевых функций на основе производственных функций.

Пример 1.Выбор оптимальной технологии производства.

Задана производственная функция для предприятия в общем виде f(x₁,x₂, ...,x_n). Однородная продукция может производиться различными производственными способами (технологиями), различающимися между собой эффективностью использования ресурсов: разнообразных материалов, затрат труда рабочих разных профессий и т.п.

Каждый производственный способ в пределах рассматриваемого периода (года) обладает фиксированной производственной мощностью, то есть максимально возможным объемом выпуска продукции.

Обозначим:

y_j— количество товара, производимоеj-м производственным способом,j=;

m_j— производственная мощностьj-го способа (ед. тов./год);

x_ij— удельные затратыi-го ресурса на единицу товара, производимогоj-м производственным способом (ед. рес.i/ед. тов.);

w_i— стоимость единицыi-го ресурса (руб./ед.рес.),;

w₀— объем фиксированных затрат по обслуживанию производства и управлению (руб./год);

Р — цена единицы продукции (руб./ед. тов);

S_j — величина прибыли, получаемая приj-м способе производства.

Задача определения выпуска различными производственными способами, обеспечивающими достижение максимальной прибыли, имеет вид:

(6.4.26)

Максимизация функции прибыли (6.4.26) осуществляется по производственным способам. Используя выражение ПФ (6.4.4), выражение (6.4.26) преобразуем следующим образом:

(6.4.27)

Или: (6.4.28)

при ограничениях на ресурсы и производственную мощность m_j:

Условие (6.4.27) максимизирует прибыль, условие (6.4.28) — объем производства по способам производства.

Пример 2.Расчет оптимального количества вовлекаемых в производство ресурсов.

Представив выражение (6.4.27) в виде

(6.4.29)

получим модель, в которой максимизация прибыли осуществляется в зависимости от объемов вовлекаемых в производство ресурсов х_i – переменных факторов ПФ. Постоянные факторыw₀ неизменны. Их наиболее эффективное использование уже отражено в ПФ. Из необходимого условия экстремумадля случая нелинейной ПФ решение задачи (6.4.29) определяется системой уравнений

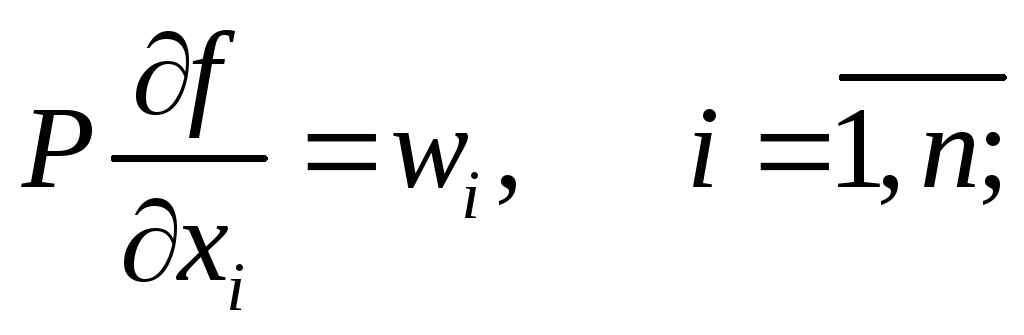(6.4.30)

где слева стоит маржинальный (предельный) доход предприятия от применения i-го фактора при фиксированных количествах прочих факторов, а справа – ценаi-го фактора.

Уравнение (6.4.30) отражает принцип вовлечения факторов предприятием, максимизирующим прибыль: оно до тех пор увеличивает количество используемого фактора, пока прирост дохода от дополнительной единицы фактора не сравняется с его ценой (при прочих равных условиях).

Поскольку производная есть функция количестваi-го фактораx_i,то условие (6.4.30) фактически описывает функцию спроса наi-й фактор со стороны предприятия, максимизирующего прибыль. Факторная модель (6.4.29) и условия порожденного спроса на факторы (6.4.30) играют главную роль при описании поведения предприятия на рынке факторов.

Пример 3. Рассмотрим функцию затрат. Используя модель (6.4.29), сформулируем следующую задачу минимизации затрат:

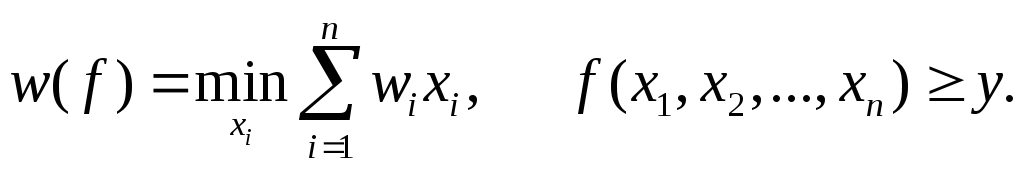. (6.4.31)

В данной модели минимизируется объем переменных затрат на производство заданного объема продукции y. Величинаy рассматривается как параметр задачи, поэтому суммарные минимально необходимые затраты являются функцией объема производстваy.