6.4. Производственные функции

Ограниченность ресурсов ставит перед обществом или отдельным человеком проблему выбора. Идет ли речь о выборе товаров или услуг для производства, или о выборе сочетания факторов капитала и труда в данном производстве, все сводится к критерию максимального денежного поступления в будущем. Выбор варианта наилучшего использования ресурсов – задача очень трудная, и в ее решении может помочь использование аппарата производственных функций. Производственная функция – это инструмент макро и микроэкономического анализа и прогнозирования, т.е. ей можно описывать как экономику страны, так и отдельную фирму.

Понятие производственной функции одной переменной.Производственная функция (ПФ) – это зависимость объема выпуска продукцииуотиспользуемогоилизатрачиваемогоресурсах (фактора производства)

у = f(x). (6.4.1)

Здесь х (х ≥ 0) и у (у ≥ 0) – числовые величины т.е. у = f(x) есть функция одной переменнойх. В связи с этим, ПФf(x) называется одноресурсной илиоднофакторной ПФ.

Показатели, в которых измеряются переменные, могут быть различными: стоимостными, натуральными, безразмерными. Иногда это не абсолютные, а относительные показатели, например производительность труда, его фондовооруженность, темпы роста и т.д. Информацией для формирования ПФ служат статистические данные, технологическая информация, данные экспериментальных исследований, экспертные оценки.

В микроэкономической теории принято считать, что у– это максимально возможный объем выпуска продукции, если ресурс затрачивается в количествех единиц. В макроэкономике такое понимание не совсем корректно: возможно при другом распределении ресурсов между структурными единицами экономической системы выпуск мог бы быть и больше. Поэтому более правильной является запись однофакторной ПФ в форме:

у = f(x,а), (6.4.2)

где а– вектор параметров структуры системы.

Пример. Возьмем ПФ в видеу = ах^b , гдеx- величина затрачиваемого ресурса ( например, рабочего времени). ПФ описывает множество производственных возможностейyв зависимости от фактораx.

Величины аиb– положительныепараметрыПФ, причем:

а > 0, 0 < b ≤ 1. (6.4.3)

В данном примере вектор параметров является двумерным вектором (а,b). ПФ описывает множество производственных возможностейyв зависимости от значения фактораx : 0 ≤ у ≤ ах^b..

График производственной функции у = ах^b изображен на рис 32.

у

На графике видно, что с ростом величины затрачиваемого ресурса хобъем выпускаурастет, однако каждая дополнительная единица ресурса дает всеменьший прирост объемавыпускаемой продукции.

0 ≤ у ≤ ах^b

х

Рис. 32

График отражает фундаментальное положение экономической теории (хорошо подтверждаемое практикой), называемое законом убывающей эффективности. Этот закон гласит, что по мере возрастания использования какого-нибудь производственного фактора (при фиксированных остальных производственных факторах), в итоге достигается точка, в которой дополнительное использование этого фактора ведет к снижению объема выпуска продукции. Закон убывающей эффективности применим на краткосрочном отрезке времени, когда по меньшей мере один производственный фактор остается неизменным.

Производственные функции нескольких переменных. ПФ нескольких переменных – это функция выпуска продукции, независимые переменныех₁, ... , х_n которой принимают значения объемов затрачиваемых или используемых ресурсов ( число переменныхnравно числу ресурсов) :

у = f(x) = f(х₁, ... , х_n). (6.4.4)

В связи с тем, что здесь x – вектор с компонентами х₁, ... , х_n , ПФ вида (6.4.4) называют многоресурсной илимногофакторной. Более правильной является запись многофакторной ПФ в форме:

у = f(x) = f(х₁, ... , х_n , а), (6.4.5)

где а– вектор параметров ПФ, (а > 0), и все факторы х_i ( i =1,...,n) по экономическому смыслу положительные.

В экономической теории чаще всего используются модели ПФ в виде нелинейного уравнения вида

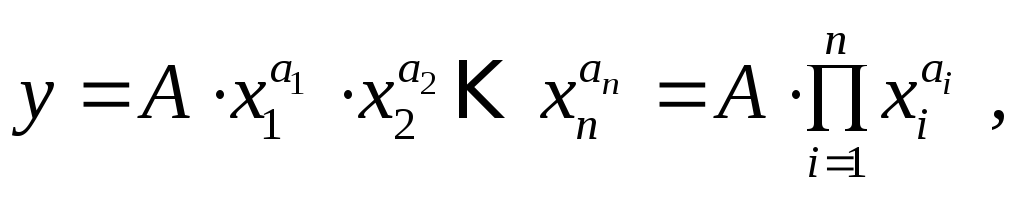(6.4.6)

где А – коэффициент пропорциональности;

а_i – показатель степени приx_i ресурсе;

x_i –затратыi-го вида ресурсов;

у – объем выпущенной продукции.

Постоянная А отражает влияние на результат прочих, не учтенных в модели факторов производства. Показатель степениа_i ( i =1,...,n) называюткоэффициентом эластичности объема производства по затратам x_i ресурса. Он показывает, на сколько увеличится объем продукции, если объем ресурсаx_iувеличивается на одну единицу.

Функция (6.4.6) имеет широкую область изменений входящих в нее параметров. К экономической области относят область изменения затрат, когда с ростом затрат ресурсов увеличивается выпуск продукции. Величина у по-разному изменяется в случае изменений количества использованных ресурсов разного вида. Если два вида ресурсов, напримерx₁иx₂изменяются по величине (один увеличивается, а другой уменьшается) и при этом величинауне изменяется, говорят о замещении одного ресурса другим.

Для отдельного предприятия, выпускающего однородный продукт, многофакторная ПФ может связывать объем выпуска с затратами рабочего времени по различным видам трудовой деятельности, различных видов сырья, комплектующих изделий, энергии, основного капитала. ПФ такого типа характеризуют действующую технологию предприятия. При построении ПФ для региона или страны в целом, в качестве величины годового выпуска y часто берут совокупный продукт (доход) региона или страны, исчисляемый обычно в неизменных ценах, а в качестве ресурсов рассматриваютосновной капитал(х₁=К) иживой труд(х₂=L) исчисляемые обычно в стоимостном выражении. Таким образом строится двухфакторная ПФy = f(К, L). От двухфакторных ПФ переходят к трехфакторным. В качестве третьего фактора иногда вводятся объемы используемых природных ресурсов.

Как уже отмечалось, для моделирования отдельного региона или страны в целом (т.е. для решения задач на макроэкономическом, а также и на микроэкономическом уровне) часто используется так называемая производственная функция Кобба – Дугласа (ПФКД). По причине важности и известности ПФКД, рассмотрим ее подробнее.

Производственная функция Кобба – Дугласа. В середине 20-х годов прошлого века американский экономист Дуглас занялся анализом статистических данных, касающихся американской обрабатывающей промышленности. Он пытался определить значение факторов, влияющих на выпуск продукции и установить связь между ними. В результате Дуглас пришел к выводу, что для производства особо важны два фактора:ТРУД и КАПИТАЛ. Причем каждый из этих факторов влияет на производство нелинейно, т.е. увеличение численности рабочих или количества оборудования на заводе не влечет соответствующего увеличения объема выпускаемой продукции.

Элементарная модель, построенная Дугласом, имела следующий вид:

. (6.4.7)

Здесь: К- объемиспользуемыхосновных фондов (или основного капитала),L-затратыживого труда,коэффициенты эффективности ресурсов,а₀ - коэффициент производительности труда

ПФКД принадлежит к классу так называемых мультипликативныхПФ (МПФ).ЛинейнаяПФ (ЛПФ) имеет вид(многофакторная ЛПФ). ЛПФ принадлежит к классуаддитивных ПФ (АПФ). Переход от МПФ к АПФ осуществляется с помощью операции логарифмирования. Для ПФКД (6.3.7) этот переход имеет вид:. Если выполнить обратный переход, то из АПФ получим МПФ.

С помощью математика Кобба, проведя регрессионный анализ большого объема статистического материала, Дуглас пришел к очень любопытному выводу. Оказалось, что с достаточно высокой точностью коэффициенты эффективности использования труда и капитала связаны между собой следующим выражением:

(6.4.8)

Таким образом, появилась производственная функция Кобба-Дугласа(ПФКД):

а₀ ≥0, 0< а <1.(6.4.9)

Это уравнение стало одним из классических в макроэкономике. Будучи впервые было опубликованным в 1934 году, ПФКД широко используется и в наши дни.

Если сумма показателей в ПФКД (6.4.7) равна единице (), то поделив выражение (6.4.7) наLее можно записать в несколько другой форме:

,т.е.:

(6.4.10)

В формуле (6.4.10) дроби иназываются соответственнопроизводительностью труда(Z)икапиталовооруженностью труда(k). Используя новые символы, получим

(6.4.11)

т.е. из двухфакторной ПФКД получим формально однофакторную ПФКД. В связи с тем, что 0< а₁ <1, из последней формулы следует, что производительность трудаZ растет медленнее его капиталовооруженности. Однако этот вывод справедлив для случая статической ПФКД в рамках существующих (неизменных) технологий и ресурсов.

Отметим, что дробь называетсяпроизводительностью капиталаиликапиталоотдачей, а обратные дробииназываются соответственнокапиталоемкостьюитрудоемкостьювыпуска.

Изучив статистические данные по американской обрабатывающей промышленности за период 1899–1922гг. Кобб и Дуглас получили следующие значения параметров ПФ (4.3.7): а₀ = 1,01;а₁ = 0,25;а₂ = 0,75. Отсюда следует, что увеличение затрат капитала на 1% вызывает приращение объема производства на 0,25%. Увеличение затрат труда на 1% соответствует увеличению объема выпуска продукта на 0,75%.

Методика построения производственных функций. При построении ПФ исследователь решает следующие задачи:

1. СпецификацияПФ — выделение существенных видов ресурсов (факторов производства) ивыбор аналитической формы функцииf(х₁, ... , х_n).

2. ПараметризацияПФ — преобразование статистических и экспертных данных с помощью регрессионного и корреляционного анализа в коэффициенты ПФ.

3. Верификация ПФ — проверка адекватности ПФ.

Выбор аналитической формы ПФ (т.е. ее спецификация) диктуется прежде всего теоретическими соображениями, которые должны явно или даже неявно учитывать особенности взаимосвязей между конкретными ресурсами (в случае микроэкономического уровня) или экономических закономерностей (в случае макроэкономического уровня), особенности реальных или экспертных данных, преобразуемых в параметры ПФ (т.е. особенности параметризации). На спецификацию и параметризацию в процессе совершенствования ПФ оказывают влияние результаты верификации. Отметим, что оценка параметров ПФ обычно проводится с помощью метода наименьших квадратов.

Пример.В табл.7 в качестве иллюстрации приведены значения параметрова₁иа₂ макроэкономической ПФКД для экономики США, рассчитанные разными авторами для разных базовых временных промежутков по различным методикам [17]. Интересно, что авторами априори не предполагалось, что обязательно.

Т а б л и ц а 7

Базовые временные промежутки (годы)	Параметры			Авторы, проводившие исследования
1899-1922	0,25	0,75	1,00	Дуглас
1914	0,36	0,61	0,97	Дуглас
1919	0,25	0,76	1,01	Дуглас
1869-1948	0,7	0,25	0,95	Валаванис
1900-1953	0,16	0,84	1	Клейн
1909-1949	0,35	0,65	1,00	Солоу
1921-1941	0,34	2,13	2,47	Тинтнер
1934-1959	0,41	0,91	1,32	Михалевский
1934-1956	0,26	0,74	1,00	Михалевский

Обращает на себя внимание, что у большинства авторов наблюдается значительное превышение параметра а₂ относительно параметраа₁. Также почти у всех авторов суммаоказалась близкой к единице.

На основании данных по экономике СССР за 1960-1985 гг. (динамики национального дохода, численности занятых в материальном производстве и объемов основных фондов), без учета НТП уравнение ПФКД для ВНП СССР имела следующий вид:

.

При подстановке фактических значений KиLза 1986 г. ошибка прогноза рассчитанного по выписанной ПФКД составила 3%. Отметим, что если параметры (факторы) ПФ оценивались во времени за периодТ, то при условии достаточно стабильной системы экстраполяция допустима на период t ≤ Т/3.

Свойства производственных функций. Производственная функцияf(х₁, х₂) как формальная конструкция определена в неотрицательном квадранте двумерной плоскости, т.е. определена при х₁≥0, х₂≥0. ПФ должна удовлетворять ряду ( для каждой конкретной ПФ – своему) свойств.

1. f(0, 0) = 0;

1'. f(0, х₂) = f(х₁, 0) = 0;

2. Если х(1) ≥ х(0), то f(х(1)) ≥ f(х(0));

2' ,;

3. ,;

3'^. ≥ 0, ;

4. f(tх₁, tх₂) = t ^p f(х₁, х₂).

Свойство 1означает, что без ресурсов нет выпуска.Свойство 1' означает, что при отсутствии хотя бы одного из ресурсов нет выпуска.

Свойство 2означает, что с ростом затрат хотя бы одного ресурса объем выпуска растет.Свойство 2' (положительность первой частной производной от ПФ) означает, что с ростом затрат одного ресурса при неизменном количестве другого, объем выпуска растет.

Свойство 3 (неположительная вторая частная производная) означает, что с ростом затрат одного (i-го) ресурса при неизменном количестве другого, величина прироста выпуска на каждую дополнительную единицуi-го ресурса не растет (закон убывающей эффективности). Свойство 3' означает, что при росте одного ресурса, предельная эффективность другого ресурса возрастает.

Свойство 4означает, что ПФ является однородной функцией степенир>0. Прир>1 с ростом масштаба производства в t раз, т.е. с переходом от векторах к векторуtх, объем выпуска возрастает вt ^p раз, т.е.имеем рост эффективностипроизводства отроста масштабапроизводства. Прир<1 имеемпадение эффективностипроизводства приросте его масштаба. Прир=1 имеемпостоянную эффективностьпроизводства приросте его масштаба(т.е. имеем независимость удельного выпуска от масштаба производства – в английской терминологииconstantreturnstoscale).

Для ПФКД (5.4.9) свойства 1-4 выполняются.

Для ЛПФ (а₀>0, а₁>0, а₂>0) свойства 1,1' и 4 не выполняются.

Учет влияния НТП. Если ПФ строится по данным временных рядов, то в качестве особого фактора роста производства может быть включен научно-технический прогресс. В зависимости от того, как изменяются используемые ресурсы и соответственно ПФ, различают следующие основные типы научно-технического прогресса:экзогенный(внешний),эндогенный(внутренний) инейтральный.

Влияние экзогенного НТП на рост национального дохода проявляется прежде всего через повышение эффективности производственных фондов в результате создания новых видов оборудования и технологий. При этом влияние НТП на объем выпуска продукта определяется рядом таких показателей, как возрастная структура основных производственных фондов, накопленный объем капиталовложений. Экзогенный НТП иногда называют общественным.

Эндогенный НТП определяется процессом роста национального дохода при неизменных затратах ресурсов. Это может происходить за счет повышения квалификации персонала, более рационального и интенсивного использования существующего оборудования и других ресурсов. Эндогенный НТП может быть назван автономным, или независимым.

НТП называют нейтральным, если он не меняет соотношения значений определенных параметров производственных факторов. При изменениях этих соотношений НТП не является нейтральным, так как в этом случае он будет материализован в одном из факторов ПФ.

В конце 1960-х годов голландский экономист Ян Тинберген ввел в формулу ПФКД величину, отображающую рост производства по мере развития научно-технического прогресса. Уравнение приобрело следующий вид:

(6.4.16)

где λ– относительный темп роста научно-технического прогресса, характеризующий темп приростаyпод влиянием НТП;t– время (в годах).

Относительный темп роста λ определяется по формуле

(6.4.17)

где Z(t) — производительность труда вt-м году;

Z(t+1) — производительность труда в(t+1)-м году.

Отметим, что если параметры ПФ оценивались по данным временных рядов продолжительностью Т₀ лет (т.е.базовый промежутокдля оценки параметров имеет продолжительность Т₀лет), то экстраполяционные расчеты по такой ПФ следует проводить не более чем на Т₀/3 лет вперед (т.е.промежуток экстраполяциидолжен иметь продолжительность не более чем Т₀/3 лет).

Производственная функция (6.4.16) – простейший пример динамическойПФ; она включает нейтральный, то есть не материализованный в одном из факторов технический прогресс. В более сложных случаях НТП может воздействовать непосредственно на производительность труда или капиталоотдачу.

Преобразуя функцию (6.4.16). Тинберген получил выражение для ежегодныхтемпов роста объема производства (в процентах):

(6.4.18)

где Y₀– темп роста объема производства (национального дохода);

К₀ – темп роста капитала;

L₀ – темп роста трудовых затрат;

λ₀ – темп роста, обусловленный НТП.

Нобелевский лауреат, американский экономист Ричард Солоу, модифицируя ПФКД, находит зависимость национального дохода от качества капитала в виде

где – производительность труда вt-м году;

– капиталовооруженность труда вt-м году.

Полученную зависимость Солоу привел к виду

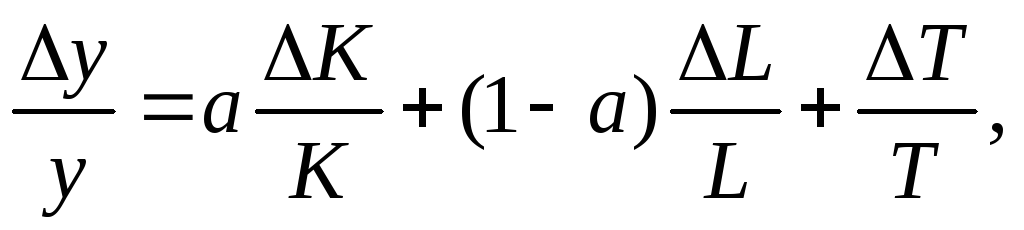(6.4.19)

где а, (1 –а) – доля капитала и труда в объеме продукта, соответственно;

ΔК – приращение капитала;

ΔL – приращение затрат труда;

Т – параметр, отражающий уровень НТП;

ΔТ – приращение параметраТ.

Уравнение Солоу выражает суммарную оценку вклада в рост объема производства затрат факторов и технического прогресса. Последний член называютостатком Солоу,отражающим вклад НТП в относительный объем приращения выпуска продукции.

Результаты, которые получил Солоу, используя свою модель при анализе экономического роста в США за период 1909 – 1949 гг., показали, что основная часть прироста национального дохода в объеме не менее трех четвертей обеспечена НТП.

Американский ученый К. Эрроу использовал для описания влияния НТП на экономическое развитие так называемый «эффект обучения». Суть его состоит в том, что научившись выполнять определенную работу, персонал способен выпускать больше продукции в единицу времени. Затраты рабочего времени на единицу изделия (τ) изменяются при этом нелинейно в виде зависимости

(6.4.20)

где b– затраты рабочего времени на выпуск первого изделия;

Q– суммарное количество выпущенных изделий;

h– модуль эластичности затрат времени на выпуск единицы продукции по суммарному объему выпуска.

Значение параметра hзависит от вида выпускаемой продукции. Так, например, Эрроу приводит следующие значения: при производстве авиационной техникиh≈ 0,7; оборудования для машиностроительных заводовh≈ 0,18; электротехнического оборудованияh≈ 0,12.

Используя эффект обучения, Эрроу построил производственную функцию для экзогенного НТП в виде

(6.4.21)

где а –постоянная величина, равная количеству единиц продукции, произведенной в единицу времени;

Кн– кумулятивный (накопленный) объем капиталовложений за определенный период времени;

L– численность трудовых ресурсов.

При использовании производственных функций следует иметь в виду их некоторую условность при оценке влияния НТП на экономический рост. Условность заключается в том, что НТП – явление многогранное, охватывающее многие стороны жизни общества, проявляющееся в самых различных формах. Это порождает при оценке много проблем и прежде всего проблему выбора системы показателей для оценки влияния НТП на экономику, технику, окружающую среду и на все человеческое общество в целом.

Производственные функции в темповой записи.Наряду со связями объемных показателей выпуска и затрат ресурсов, с помощью ПФ могут быть рассмотрены связи между темпами прироста этих показателей. Рассмотрим получение этих связей на примере динамической ПФ Кобба-Дугласа с нейтральным техническим прогрессом

(6.4.22)

где λ– относительный темп роста научно-технического прогресса, t – время (в годах).

Пусть величины KиLявляются непрерывными дифференцируемыми функциями времени. В таком случае они представляют не объемы использованных ресурсов за определенный период времени, аинтенсивностиих использованияв каждый моментвремени.

Прологарифмируем функцию (6.4.22):

.(6.4.23)

Продифференцируем полученное выражение:

. (6.4.24)

Здесь: 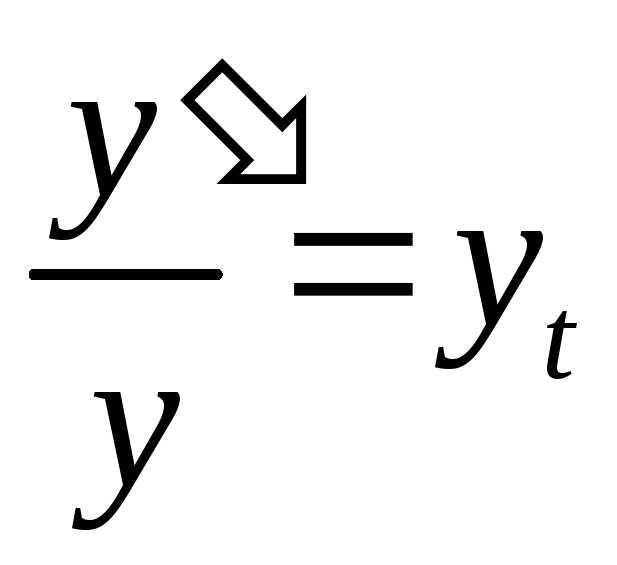;;– непрерывные темпы прироста выпуска, капитала и труда соответственно. Таким образом, производственной функции в объемных показателях (6.4.22) соответствует линейная зависимость темпов прироста:

. (6.4.25)

Эта зависимость называется производственной функцией Кобба-Дугласа в темповой записи. Линейная функция (6.4.25) характеризует вклад темпов прироста факторов производства в общие темпы прироста выпуска. Показатель λ - свободный член ПФКД в темповой записи – это темп нейтрального (т.е. не материализованногов одномфакторе) технического прогресса. Это та часть темпа прироста выпуска, которая не связана с приростом затрат капитала и труда, а отражает интенсификацию производства на макроуровне.

Пример. Допустим, ПФ в темповой записи имеет вид:

.

Пусть при этом средний темп прироста затрат труда l_t составил 1%, средний темп прироста используемого капиталаk_t=6%, средний темп прироста выпускаy_t=3,9%.

Тогда вклад в средний темп прироста выпуска y_t экстенсивных факторов – прироста затрат капитала и труда – составляет

от k_t:0,3 * 6 =1,8 (46,1%);

от l_t: 0,6 * 1= 0,6 (15,4 %).

Суммарная доля вклада экстенсивных факторов =61,5% и, соответственно, доля интенсивного фактора (технического прогресса) в прирост y_t составляет

.

Таким образом, основной эффект в увеличение темпов прироста выпуска продукции в данном примере дают инвестиции в основные капиталы – 46,1%. Влияние развития научно-технический прогресса (НТП) оценивается в 38,5%.