Для учета запаздывания на освоение опф τu к уравнению развития мощности ппо (10.2.3) следует добавить уравнение инерционного запаздывания освоения опф

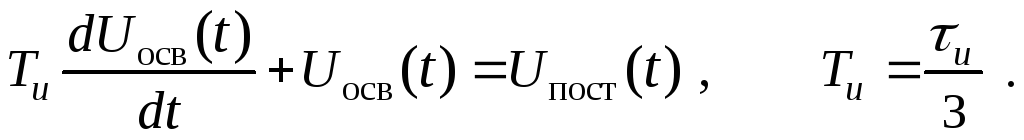(10.2.7)

с учетом инерционного запаздывания на производство продукции, уравнение выпуска принимает следующий вид:

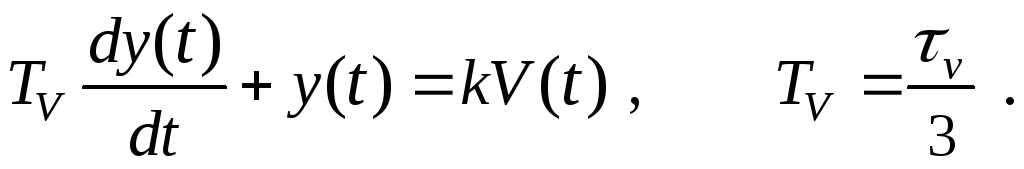(10.2.8)

Модель распределенного запаздывания является более общей и адекватной и чистое запаздывание вытекает из нее как частный случай. Однако, ввод в модель простого производственного объекта (10.1.23) уравнений инерционного запаздывания, приводит к существенному повышению размерности системы дифференциальных уравнений динамической модели производственного объекта, что приводит к вычислительным затруднениям.

Экспоненциальное запаздывание первого порядка достаточно хорошо характеризует переходные режимы многих реальных экономических процессов. Однако в некоторых случаях, для моделирования запаздывания порождаемого, например, психологической инерцией потребителей, более адекватной является модель, образованная дифференциальным уравнением второго порядка, в которой отсутствует скачок производной функции в момент t=0 как на рис.52.

10.3. Модель замкнутой производственной системы

В данном параграфе рассмотрим экономические системы на базе ППО, элементы которых взаимодействуют друг с другом и образуют замкнутую систему. Вначале составим модели элементов такой рыночной системы.

модели элементов экономических систем. Получим несколько простых динамических моделей экономических элементов, которые можно использовать в рыночной модели, где необходимо учитывать хранение, транспортировку, сбыт и многое другое в процессе деятельности предприятия.

1. Модель склада. Предположим, что после изготовления продукция предприятия отправляется на склад, откуда затем вывозится.

На рис.53: – поток поступающей на склад продукции,

–поток вывозимой продукции,

– количество хранящейся на складе продукции.

СКЛАД

Рис.53

В принятых обозначениях запишем уравнение склада

(10.3.1)

где – количество продукции на складе в начальный момент.

Аналогично можно записать уравнения для складов основных и оборотных производственных фондов.

2. Модель транспортировки. Транспортировка занимает определенное время, зависящее от расстояния между объектами и способа транспортировки. Будем считать, что при перевозке качество продукции не претерпевает изменений. Поэтому транспортировку будем учитывать через чистое запаздывание равное времени перемещения продукции в пункт ее потребления.

(10.3.2)

где – поток загружаемой на транспорт продукции, а– поток доставленной продукции в пункте назначения. Коэффициентхарактеризует потери продукции при транспортировке.

3. Модель реализации. Готовая продукция может реализовываться немедленно или этот процесс может затягиваться на время реализации В зависимости от способа, процесс реализации можно описать как чистое запаздывание:

(10.3.3)

или как инерционное запаздывание:

(10.3.4)

где – поток поступившей на реализацию продукции,– поток реализованной продукции.

4. Модель банка. После продажи, произведенная на предприятии продукция имеет обратное влияние на производственный объект, которое в основном осуществляется через выручку, поступившую в распоряжение предприятия.

Пусть – продажная цена единицы продукции. Тогда поток денегот реализованной продукции

(10.3.5)

поступает в банк на расчетный счет предприятия. Если – количество денег предприятия в банке в момент времениt, а – поток денег, снимаемых с банка предприятием, то уравнение банка имеет вид:

(10.3.6)

где – количество денег предприятия в банке в начальный момент времениt₀. Формально, с математической точки зрения простейшая модель банка совпадает с моделью склада.

Модель взаимодействия ППО с рынком. На рис.54 представлена элементарная схема взаимодействия ППО с рынком.

U(t)

ППО

y(t)

РЫНОК

V(t)

Рис.54

На рисунке:

– поток денег, идущих на приобретение ОПФ,

– поток денег, идущих на приобретение оборотных фондов,

– поток денег, идущих на остальные потребности (зарплата, соцкультбыт, налоги и др.),

– цены единицы изделия, основных и оборотных фондов,

– доли потока денег, выделяемых на приобретение основных и оборотных фондов,–доля оставшегося потока денег:

В схеме не учитывается запаздывание на складирование, транспортировку, сбыт, банковские операции и другие рыночные операции. также не учитываются важные маркетинговые мероприятия, такие, например, как формирование спроса и предложения, ценообразование, реклама и многое другое. Схема является простейшей базовой моделью взаимодействия ППО с рынком, которую в дальнейшем можно сколько угодно наращивать и усложнять.

Запишем систему соотношений, описывающую представленную на рис.54 замкнутую систему с учетом временного лага на цикл производства.

Модель ППО:

(10.3.7)

Модель рынка:

(10.3.8)

Условия равновесного рынка. Используя соответствующие уравнения из системы (10.3.8) выражения потоков ОПФ и Обф можно записать:

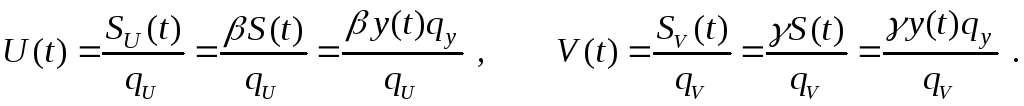(10.3.9)

В случае, когда коэффициент фондоемкости m(t)=m=Const, подставляя (10.3.9) в уравнения ППО (10.3.7), получим:

(10.3.10)

В условиях стабильного (равновесного) рынка, любые возмущения внутри рынка, не должны отражаться на производственной деятельности предприятия, т.е. поток выпуска продукции должен оставаться неизменным. Получим условия стабильной работы ППО. Будем считать, что предприятие работает на полную мощность, т.е. В этом случае,, и система уравнений (10.3.10) примет вид

откуда следуют условия стабильного (равновесного) рынка

(10.3.11)

при изменении экзогенных рыночных факторов (например, изменения цен на производственные фонды q_U и q_V,), из условий (10.3.11) можно определить значения управляемых эндогенных параметров (например, цену своей продукции q_у, величины долей β и γ), которые обеспечат стабильную работу предприятия в рамках рассмотренной модели.

М

q_y

одель замкнутой системы с учетом спроса и предложения.Построим упрощенную имитационную модель, описывающую взаимодействие спроса, производства и управления на уровне ППО. Схема этой модели приведена на рис.55.

2

–

U

q_y

ε

1

3

4

5

V

–

Рис.55

В схеме приняты следующие обозначения:

–потребное количество продукции предприятия в единицу времени;

(t)–спрос на продукцию предприятия в единицу времени;

ε(t)– величина невязки (рассогласования) между потоками потребности и спроса на продукцию предприятия

;

1 — блок формирования цены продукции. Цена рассчитывается как функция невязки. В простейшем случае, это может быть пропорциональная зависимость вида

где q₀ – базовая цена при ε(t) = 0, – коэффициент пропорциональности.

2 — блок определения потока отложенного спроса на продукцию предприятия. Величина отложенного спроса зависит от рыночной цены изделия и других факторов маркетинга. Она определяется путем маркетинговых исследований рынка. Например, функция отложенного спроса может моделироваться как:

где – запаздывание реакции покупателей на изменение цены, – коэффициент пропорциональности.

3 — блок определения величины потока потенциального предложения предприятия по выпуску продукции:. Предложение (готовность предприятия к производству изделия в количестве за единицу времени) в основном зависит от ценыизделия и определяется в соответствии с известной кривой предложения

4 — блок расчета потребных потоков ОПФ и ОбФдля производства продукции в объеме(t). Если предприятие работает на полную мощность, т.е. то из уравнений ППО следует:

где и– максимально допустимые потоки основных и оборотных фондов, зависящие от финансовых возможностей предприятия.

Если судить по динамике потребности и выпуска продукции, то, очевидно, что колебания потребности вызывают колебания выпуска . Возникает естественный вопрос: не может ли производство само быть источником колебаний? Ответить на этот вопрос можно исследуя процессы в модели, представленной на рис.55. Из-за колебаний в развитии производства наряду с колебаниями цены возникают колебания отложенного спроса и других эндогенных переменных модели. Расчеты показывают, что колебательность системы и ее устойчивость сильно зависят от экзогенных параметров и.

10.4. Многопродуктовый простой производственный объект

Модель развития многопродуктового объекта. Обычно производственные предприятия выпускают не единственный или однородный вид продукции. Тогда предприятие представляет собой многопродуктовый производственный объект (МППО). Как и в случае с ППО, при рассмотрении МППО выделим два входных потока: потоки ОПФ U(t) и ОбФ V(t) и поток выпуска продукции В отличии от модели ППО (рис.53), для МППО эти потоки представляют собой векторные величины (рис.56).

М П П О

Рис.56

Введем в рассмотрение вектор количества ОПФ на предприятии

(10.4.1)

и коэффициент мгновенной фондоемкости , равный количеству ОПФr-го вида, необходимых для выпуска единицы j-го изделия в единицу времени. Тогда возможный поток выпуска продукции j-го вида в единицу времени (мощность предприятия),ограниченный количеством ОПФ r-го вида выделенных на производство j-го изделия , будет иметь вид:

(10.4.2)

Общее потребное количество ОПФ r-го вида для производства всех изделий равно сумме

(10.4.3)

Дифференцируя выражение (10.4.3), перейдем к потокам поступающих и выбывающихосновных производственных фондов:

(10.4.4)

где – коэффициент пропорциональности. Уравнение (10.4.4) является уравнением развития основных производственных фондов предприятия.

Используя выражение коэффициента выбытия ОПФ для многопродуктового производственного объекта с учетом (10.4.2), из уравнения (10.4.4) получим уравнение мощности по выпуску предприятиемj-ой продукции из условия наличия на предприятии ОПФ r-го вида:

(10.4.5)

где – количество ОПФr-го вида, направленных на производство j-го изделия.

Мощность предприятия по выпуску j-го изделия определяется наиболее дефицитной компонентой ОПФ, т.е.

(10.4.6)

где компоненты вектора мощности , находятся из решения системы уравнений (10.4.5).

Модель выпуска продукции МППО. Обозначим – поток оборотных фондовs-го вида потребляемых предприятием для производства j-ой продукции. Вектор потока оборотных фондов, потребных для производства j-ой продукции

является вектором с пропорциональными компонентами.

Общий поток потребляемых оборотных фондов s-го вида для идеального производства определяется как сумма

(10.4.7)

По аналогии с уравнением выпуска продукции на ППО, выпуск продукции на многопродуктовом простом производственном объекте с учетом чистого запаздывания на производство, можно записать в виде уравнения:

(10.4.8)

где: – поток продукцииj-го изделия, зависящий от величины потока оборотных фондов (ОбФ) s-го вида;

–коэффициент фондоотдачи ОбФ s-го вида на производстве j-го изделия: ;

–запаздывание, учитывающее время производства j-го изделия при использовании s-го вида ОбФ.

Поток выпуска готовой продукции j-го вида в момент времени t учетом ограничения на располагаемую мощность предприятия определяется из системы:

(10.4.9)

где поток продукции определяется из уравнения (10.4.8), а располагаемая мощность– из условия (10.4.6).