По статистическим точкам строятся функции Фос(t) иРс(t).На рис.46, 47 эти функции заданы в простой линейной форме

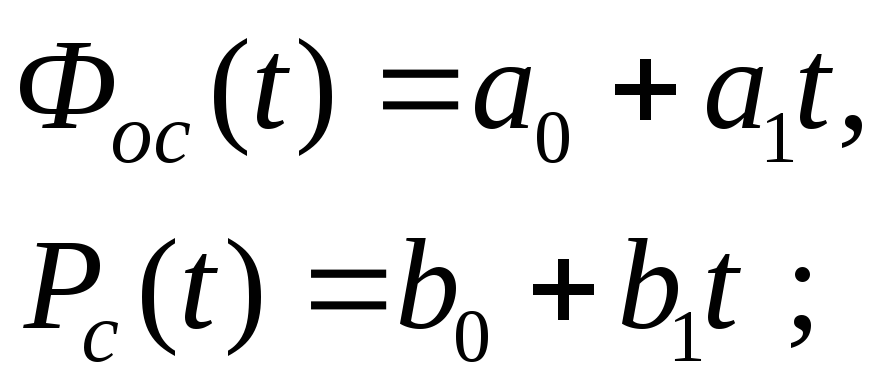(10.1.16)

где коэффициенты определяются методом наименьших квадратов. Подставляя (10.1.16) в формулу коэффициента фондоемкости (10.1.1) получим выражение m_с(t), идентифицирующее значение m(t) на базе статистического материала:

(10.1.17)

Замечание. Если на предприятии не внедряются новые технологии и более современное и совершенное оборудование на базе НТП, то можно заметить, что по формуле (10.1.1) количественное изменение ОПФприводит к пропорциональному изменению мощностии их частноеm(t) остается практически постоянным. Действительно, для крупных объектов на небольших интервалах времени фондоемкость мало зависит от времени. В монографии Т.К.Сиразетдинова [22] приводится график коэффициента фондоемкости промышленности США за период с 1890 по 1960 годы. Из графика видно, что в 1890–1935 годы фондоемкость оставалась примерно на значенииm=3,2 , а в 1945–1960m=1,85. Очевидно, что существенное уменьшение коэффициента фондоемкости связано с интенсификацией промышленного производства в условиях военного времени.

2. Идентификация коэффициентавыбытия ОПФ α(t). Для статистической идентификации α(t) можно воспользоваться выражением α(t) из формулы (10.1.7): α(t) = U_В (t) / Р (t).

Собрав статистику по выбытию ОПФ на базовом периоде и записав ее, например, в виде линейной регрессии

получим выражение для определения коэффициента выбытия

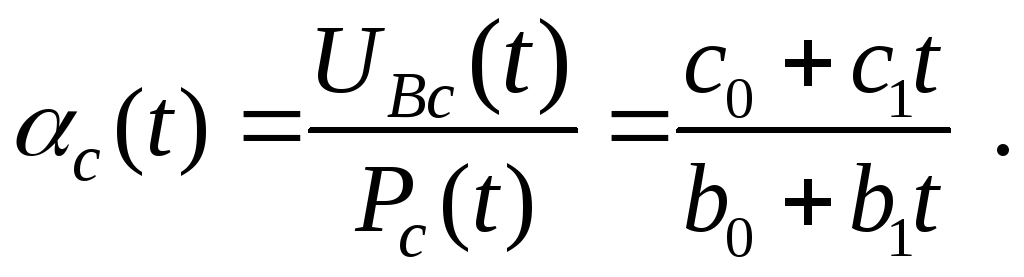
Коэффициенты модели объекта желательно ежегодно корректировать на основе новой поступающей информации о состоянии объекта.

Механический аналог уравнения мощности. Чтобы лучше понять природу экономических параметров и характеристик, используем широко применяемый в физике и технических науках метод аналогий.

Рассмотрим ППО работающий на полную мощность. Через обозначим общее (суммарное) количество продукции, произведенной объектом за рассматриваемый период времени. Тогда мощность объектаопределяется как производная

и уравнение мощности (10.1.8) можно записать в следующем виде:

(10.1.18)

Запишем известное в механике одномерное уравнение движения материальной точки переменной массы M(t),движущейся по осиОХ под действием силыF в среде с коэффициентом сопротивления (демпфирования)ξ:

(10.1.19)

Сравнивая уравнение мощности Ппо (10.1.18) и уравнение движения точки переменной массы (10.1.19) можно сделать вывод о наличии между ними математической аналогии. Обозначим скорость движения материальной точки и сведем видимые аналогии в таблицу 16.

Т а б л и ц а 16

А Н А Л О Г И И
Экономический объект	Механический объект
Р(t) - мощность Y(t) – полный объем выпуска m(t) - фондоемкость α(t) – коэффициент выбытия ОПФ U(t) – поток поступления ОПФ Ф(t) = mP – количество ОПФ	V(t) – скорость движения X(t) – пройденный путь M(t) - масса ξ(t) – коэффициент сопротивления F(t) – движущая сила K=MV – количество движения

Уравнение выпуска продукции. Воспользуемся введенными ранее понятиями потока поступающих на ППО оборотных фондов V(t) и потока выпускаемой ППО продукции у(t). Составим отношение

где – коэффициент мгновенной фондоемкости оборотных фондов по выпуску данной продукции. Он характеризует количество оборотных фондов, необходимых для выпуска единицы продукции.