ММИЭ / Лаб.раб. ММИЭ (Рафаилов) / Лабораторная работа №6

Лабораторная работа №6

МНОГОПРОДУКТОВЫЙ ПРОСТОЙ

ПРОИЗВОДСТВЕННЫЙ ОБЪЕКТ

Цель работы: изучение математической модели многопродуктового производственного объекта. Закрепление теоретического материала расчетом примеров определения возможностей объекта по выпуску продукции различного вида.

Требуется определить:

1. Количество изделий каждого вида Y_j, которое предприятие сможет выпустить, исходя из наличия компонент.

2. Необходимую численность персонала L_j для выпуска каждого вида изделий.

Исходные данные

Вариант

Компо-ненты	Изделия
	А1	А2	А3	А4
a1	2	11	0	1
a2	6	0	0	19
a3	0	2	1	1
a4	1,1	2	7	3
a5	2	1	1	1

N1	N2	N3	N4	V10	V20	V30	V40	V50	L0	mL1	mL2	mL3	mL4
0,6	0,1	0,1	0,2	31	15	18	40	19	6	0,4	1,4	1	1,3

Метод решения

Задано:

n-количество видов изделий;

А_i – вид изделия;

аⁱ – нормы затрат на изготовление единицы каждого изделия;

N_j – доли выпуска каждого вида изделия в общем объеме выпуска;

V_i0 – ограничения на наличие компонент;

L₀ – ограничение на наличие персонала;

m_Lj – нормативы трудозатрат на изготовление изделия каждого вида.

Предприятие, выпускающее несколько видов продукции, называется многопродуктовым производственным объектом. Рассмотрим влияние на процесс производства двух факторов производства – материальных и трудовых затрат.

1. Материальные затраты на производство продукции

Предположим, что всего при производстве продукции используется m видов компонент aⁱ (i=1,2,...,m ) и каждое изделие A_j состоит из различных компонент, которые обозначим через aⁱ_j, i = 1,2,...,m, j = 1,2,...,n . Здесь индекс j означает принадлежность компоненты aⁱ к продукции (изделию) вида A_j., а индекс i означает вид компоненты aⁱ_j (например, материалы, энергия или более конкретно, колесо, корпус машины и т.д.). Вообще говоря, необязательно, чтобы все виды компонент aⁱ_j входили во все виды изделий A_j.

Количество i-го компонента, используемого для изготовления единицы j-го вида выпускаемой продукции, обозначим через . Потребное количество в единицу времени компоненты aⁱ_j для выпуска продукции A_j в количестве Y_j обозначим через Тогда

(1)

Величина (компоненты затрат при производстве изделия A_j ) для каждого фиксированного значения индекса j представляет собой вектор с пропорциональными компонентами, т.е.

(2)

Если ресурсы объекта не соответствуют пропорции (2), то выпуск определяется наличием наиболее дефицитного вида ресурса:

(3)

где – имеющиеся на объекте ресурсы i –го вида.

2. Трудовые затраты при производстве продукции

В зависимости от вида выпускаемых изделий, применяемой технологии и используемого оборудования требуется для производства продукции в количестве Y_j требуется соответствующее количество рабочей силы различных специальностей, которые образуют вектор с пропорциональными компонентами () при фиксированном j , т.е.

(4)

где  численность производственного персонала p-й специальности, занятой на производстве j- го изделия;

 норматив трудозатрат на единицу изделия A_j ;

P_j  общее число различных специальностей, необходимых при изготовлении изделия A_j.

Обычно имеются ограничения на численность персонала

(5)

Общее количество персонала обозначим через L₀.

Если трудовые ресурсы объекта не соответствуют пропорции (4), то выпуск определяется наличием наиболее дефицитного вида ресурса:

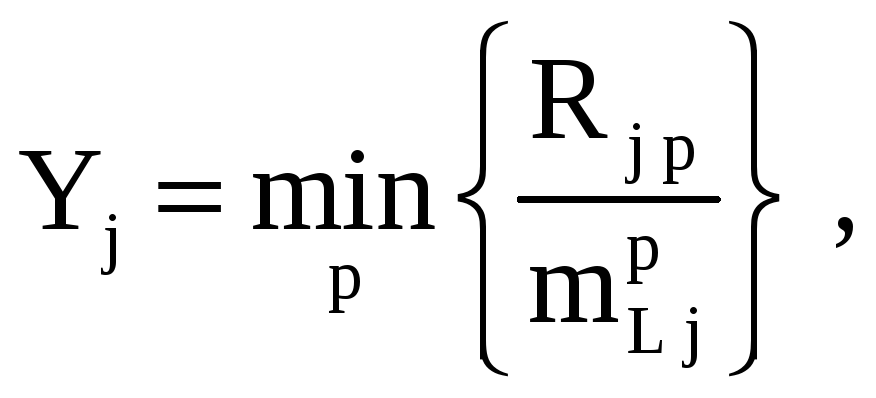
где - имеющиеся на объекте людские ресурсы p-го вида.

РЕШЕНИЕ

Решим задачу определения возможностей многопродуктового производственного объекта по наличию материальных и трудовых ресурсов.

1. Определим количество изделий каждого вида Y_j, которое предприятие может выпустить, исходя из наличия компонент.

1. Для заданного количества компонент a_i (i=1,…,5) запишем систему неравенств

V₁=a₁¹y₁ + a₂¹y₂ + a₃¹y₃ + a₄¹y₄ ≤V₁₀

V₂=a₁²y₁ + a₂²y₂ + a₃²y₃ + a₄²y₄ ≤V₂₀

V₃=a₁³y₁ + a₂³y₂ + a₃³y₃ + a₄³y₄ ≤V₃₀ (6.1)

V₄=a₁⁴y₁ + a₂⁴y₂ + a₃⁴y₃ + a₄⁴y₄ ≤V₄₀

V₅=a₁⁵y₁ + a₂⁵y₂ + a₃⁵y₃ + a₄⁵y₄ ≤V₅₀

В систему уравнений (6.1) подставим y_j = N_jY получим

Y[a₁¹N₁ + a₂¹N₂ + a₃¹N₃ + a₄¹N₄] ≤V₁₀

Y[a₁²N₁ + a₂²N₂ + a₃²N₃ + a₄²N₄] ≤V₂₀

Y[a₁³N₁ + a₂³N₂ + a₃³N₃ + a₄³N₄] ≤V₃₀

Y[a₁⁴N₁ + a₂⁴N₂ + a₃⁴N₃ + a₄⁴N₄] ≤V₄₀

Y[a₁⁵N₁ + a₂⁵N₂ + a₃⁵N₃ + a₄⁵N₄] ≤V₅₀

Определим ограничение на суммарный выпуск продукции Y

Y₁[2*0,6+11*0,1+0*0,1+1*0,2] ≤ 31

Y₂[6*0,6+0*0,1+0*0,1+19*0,2] ≤ 15

Y₃[0*0,6+2*0,1+1*0,1+1*0,2] ≤ 18

Y₄[1,1*0,6+2*0,1+7*0,1+3*0,2] ≤ 40

Y₅[2*0,6+1*0,1+1*0,1+1*0,2] ≤ 19

2,5Y₁ ≤ 31

7,4Y₂ ≤ 15

0,5Y₃ ≤ 18

2,16Y₄ ≤ 40

1,6Y₅ ≤ 19

Y₁ ≤ 12,4

Y₂ ≤ 2,03

Y₃ ≤ 36

Y₄ ≤ 18,52

Y₅ ≤ 11,88

Выбираем наименьшее значение Y=Y_min = Y₂.

Для 4 видов изделий вычислим количество выпускаемой продукции y_j.

y₁=N₁*Y_min=0,6*2,03=1,20

y₂=N₂*Y_min=0,1*2,03=0,20

y₃=N₃*Y_min=0,1*2,03=0,20

y₄=N₄*Y_min=0,2*2,03=0,40

Дефицитной компонентой, которая ограничивает выпуск продукции, является V₂₀.

Расчет потребного количества компонент

Подставляем найденные значения y₁, y₂, y₃, y₄ в систему (6.1) и рассчитаем V_{потребное}.

V¹_{потребное} = 2*1,20+11*0,20+0*0,20+1*0,40=2,4+2,2+0+0,4=5

V²_{потребное} = 6*1,20+0*0,20+0*0,20+19*0,40=7,25+0+0+7,75=15

V³_{потребное} = 0*1,20+2*0,20+1*0,20+1*0,40=0+0,40+0,20+0,40=1

V⁴_{потребное} = 1,1*1,20+2*0,20+7*0,20+3*0,40=1,320+0,40+1,4+1,20=4,32

V⁵_{потребное} =2*1,20+1*0,20+1*0,20+1*0,40=2,40+0,20+0,20+0,40=3,20

Вычислим количество излишек по каждой компоненте:

V₁ =V₁₀-V¹_{потребное} = 31-5=26

V₂ =V₂₀-V²_{потребное} = 15-15=0

V₃ =V₃₀-V³_{потребное} =18-1=17

V₄ =V₄₀-V⁴_{потребное} = 40-4,32=35,68

V₅ =V₅₀-V⁵_{потребное} = 19-3,20=15.8

После производства каждого вида изделия на складе остаются компоненты a₁, a₂, a₃, a₄ , которые можно продать, получив дополнительную прибыль.

II. Вычислим потребное количество персонала

На производстве изделий работают 6 рабочих одинаковой специальности, то есть L₀=6.

Имеется ограничение на общую численность персонала

L_{потребное} =∑ m_Lj * Y_j

L¹_п = m_L1*y₁ = 0,4*1,20=0,5(=1)

L²_п = m_L2*y₂ = 1,4*0,2=0,3 (=1)

L³_п = m_L3*y₃ = 1*0,2=0,2(=1)

L⁴_п = m_L4*y₄ = 1,3*0,4=0,5(=1)

L_{потребное} = L¹_п + L²_п + L³_п + L⁴_п = 1+1+1+1=4

L=L₀ – L_{потребное} =6-4=2

2 рабочих простаивают при изготовлении изделий, а 4 других загружены не полностью.

ВЫВОД

После изучения математической модели многопродуктового производственного объекта получили, что дефицитная компонента, которая ограничивает выпуск продукции равна V₂₀ = 15. После подсчета потребного количества компонент получили, что компонента а² расходуется полностью, а часть компонент а¹, а³, а⁴, а⁵ остаются на складе.

Дробность программы выпуска y₁=1,20; y₂=0,20; y₃=0,20; y₄=0,40 означает, что за рассматриваемую единицу времени изготавливается не целое число изделий, некоторые из них изготовлены частично. Расход каждого вида компонент равен V¹=5, V²=15, V³=4,32, V⁴=3,20. Излишки этих компонент можем продать и получить дополнительную прибыль.

Пусть нормативы трудозатрат равны m_L1=0,4; m_L2=1,4; m_L3=1; m_L4=1,3. Тогда потребная численность персонала по каждому виду изделия равна L¹_п = 0,5, L²_п =0,3, L³_п =0,2, L⁴_п = 0,5.

Значение потребной численности для выпуска каждого изделия дробное. Это означает, что люди, работающие на сборке каждого изделия, загружены не полностью. Таким образом, необходимое количество персонала на участке составляет 4 человека, при недогрузке персонала 0,5; 0,7; 0,8; 0,5 или при восьмичасовом рабочем дне – 4 часа, 5,6 часов, 6,4 часов, 4 часа. При имеющемся ограничении L₀=6 человек, видно, что 2 рабочих будут простаивать. Эти рабочие должны быть переведены на изготовление других изделий или уволены.

59