
6269
.pdf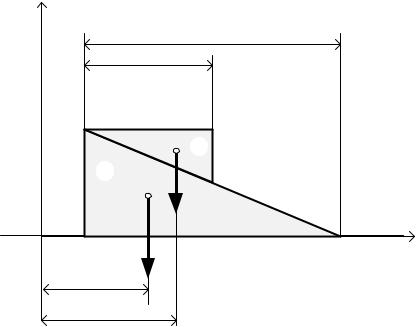
20
n
Если ∑ Fkxe = 0 , то из теоремы получаем, что &&xC = 0 . Отсюда следует, что
k =1
+,H , *EFG
(центр масс движется по оси x равномерно или покоится).
Задача 2.1. На неподвижную однородную призму А, лежащую на горизонтальной плоскости, положили однородную призму В. Ширина основания призмы А равна a. Ширина основания призмы В равна b. Пренебрегая трением, определить смещение призмы А после того, как призма В опустится по призме А. Принять, что масса призмы В втрое меньше массы призмы А.
Решение.
Введем неподвижную систему координат Оху. В этой системе координат обозначим за х1 и х2 координаты центров масс призм А и В в начальный момент времени (рис. 6). Смещение по горизонтали, призмы А обозначим S.
y
a
b
|
|
B |
|
|
A |
|
|
O |
P |
P2 |
x |
1 |
|
|
x1
x2
Рис.6
Смещение в процессе движения верхней призмы В относительно нижней призмы А будет равно (a-b). Тогда смещение верхней призмы относительно неподвижной системы координат составит S+(a-b).
В конечный момент времени координаты центров масс призм А и В будут соответственно равны
′ |
= x1 + S, |
′ |
= x2 + S + (a − b). |
x1 |
x2 |
В данной задаче имеем механическую систему, состоящую из двух тел: однородных призм А и В. Внешними силами, приложенными к системе
21
являются силы тяжести: Р1 и Р2 и реакция гладкой поверхности основания призмы А, направленная по вертикали (на рисунке не показана). Все эти внешние силы вертикальны, поэтому сумма их проекций на горизонтальную ось равна нулю.
В соответствии со следствием 2 из теоремы о движении центра масс делаем вывод: поскольку сумма проекций внешних сил на ось х равна нулю, то
n
∑ Fkxe = 0 , то x&C = const.
k =1
Поскольку в начальном состоянии система покоится, то
+, *EFG .
Запишем выражение для определения положения центра масс в начальном положении системы:
x = |
x m + x m |
= |
x P + x P |
|||
1 1 |
2 2 |
1 1 |
2 2 |
. |
||
m + m |
|
|
||||
C |
|
P + P |
||||
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
Запишем выражение для определения положения центра масс в конечном положении системы с учетом изменения начальных координат точек приложения сил Р1 и Р2:
|
′ |
′ |
|
′ |
′ |
|
( |
x + S |
) |
P + |
( |
x + S + (a − b) |
) |
P |
||
|
x m |
+ x m x P |
+ x P |
|
1 |
1 |
|
2 |
2 |
|
||||||
x = |
1 1 |
2 2 |
= |
1 1 |
2 2 |
= |
|
|
|
|
|
. |
||||
C |
m + m |
|
P + P |
|
|
|
|
|
P + P |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
|
1 |
2 |
|
|
|
Так как знаменатели в этих выражениях равны, то приравняем числители дробей:
x P + x P = ( x + S ) P + ( x + S + (a − b)) P , |
||||||||
1 |
1 |
2 |
2 |
1 |
1 |
2 |
|
2 |
Упрощая полученное равенство, получим: |
|
|
|
|
||||
( P + P ) S + P (a − b) = 0. |
|
|
||||||
|
1 |
|
2 |
2 |
|
|
|
|
Решая полученное уравнение относительно неизвестной переменной S, получим |
||||||||
|
I |
J ' K |
|
|
' K |
. |
||
|
J J |
|
4 |
|||||
Смещение призмы В получилось отрицательным, это значит, что она сместится влево.
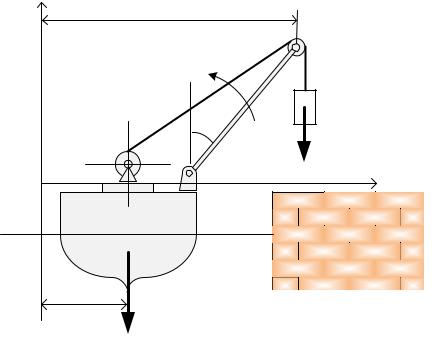
Задача 2.2. Определить перемещение S плавучего крана, поднимающего груз весом Р1=2т, при повороте стрелы крана на 300 до вертикального положения (рис. 7). Вес крана Р2=20т; длина стрелы l =8 м. Сопротивлением воды пренебречь.
22
y |
x2 |
|
|
|
A |
|
30° |
|
P2 |
O |
x |
|
P
x1
1
Рис.7
Решение.
Вданной задаче имеем механическую систему, состоящую из двух тел: плавучего крана и груза. Внешними силами, приложенными к системе являются
вес крана Р1, вес груза Р2 и давление воды, направленное снизу вверх (на рисунке не показано). Все эти внешние силы вертикальны, поэтому сумма их проекций на горизонтальную ось равна нулю.
Всоответствии со следствием 2 из теоремы о движении центра масс делаем вывод: поскольку сумма проекций внешних сил на ось х равна нулю, то
n |
|
|
|
e |
& |
|
|
∑ Fkx = 0 , и |
= const. |
|
|
xC |
|
||
k =1 |
|
|
= 0 , |
|
|
& |
|
Поскольку в начальном состоянии система покоится, то xC |
|||
и следовательно, центр тяжести системы по оси х не перемещается, то есть
xC = const.
Введем неподвижную систему координат Оxy (см. рис. 7).
Запишем выражение для определения положения центра масс в начальном положении системы:
x = |
x m + x m |
= |
x P + x P |
|||
1 1 |
2 2 |
1 1 |
2 2 |
. |
||
m + m |
|
|
||||
C |
|
P + P |
||||
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
Запишем выражение для определения положения центра масс в конечном положении системы с учетом изменения начальных координат точек приложения сил Р1 и Р2:
x = |
x¢m + x¢m |
= |
x¢P + x¢P |
= |
( x + S ) P + ( x + S -l ×sin 30°) P |
||||
1 1 |
2 2 |
1 1 |
2 2 |
1 |
1 2 |
2 . |
|||
C |
m + m |
|
P + P |
|
|
P + P |
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
|
1 |
2 |

23
Так как знаменатели в этих выражениях равны, то приравняем числители дробей:
x P + x P = ( x + S ) P +( x + S -l ×sin 30°) P , |
|||||||
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
Упрощая полученное равенство, получим:
( P + P ) S - P l ×sin 30° = 0. |
||
1 |
2 |
2 |
Решая полученное уравнение относительно неизвестной переменной S, получим
S = |
P l ×sin 30° |
= |
2×8×0.5 |
= 0.36(м). |
|
|
|||||
2 |
|
|
|
|
|
||||||
(P + P ) |
22 |
|
|
|
|||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
Задача 2.3. Тело массой m = 2 кг |
|
|
|
|
|
|
S |
|
|
||
движется по горизонтальным |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направляющим согласно закону |
|
|
|
|
|
|
|
|
|
|
|
s = 2t2 + 1. |
|
|
|
|
|
|
|
|
|
|
|
Определить модуль главного вектора |
|
|
|
|
O |
|
|
|
|
||
внешних сил, действующих на тело. |
|
|
|
|
|
|
|
|
|||
Решение.
Из формулировки теоремы о движении центра масс
, @ вA ?в,
AB
следует справедливость равенства соответствующих модулей:
maC = Re
Вычислив ускорение центра масс по формулем |
, |
|
|
|
|
|
', G M 4 |
|
|
|
|
|
|
с |
|
|
|
|
|
|
определим модуль главного вектора внешних сил: |
|
|
||||
Re = ma = 2 × 4 = 8( |
кг × м |
) = 8 (Н ). |
|
|
||
|
|
|
||||
C |
|
с2 |
|
|
||
Задача 2.4. Диск массой m = 20 кг |
|
|
|
|
|
|
вращается равномерно вокруг неподвижной оси с |
ω |
|||||
угловой скоростью ω = 10 рад/с. |
|
|
|
|
||
|
|
|
|
O C |
||
Определить модуль главного вектора внешних |
||||||
сил, приложенных к диску, если его центр |
|
|
|
|||
|
|
|
||||
тяжести удален от оси вращения на расстояние |
|
|
||||
ОС = 5 см. |
|
|
|
|
|
|
Решение.
В процессе движения цент масс диска движется по окружности, центром которой является точка О. По условию задачи вращение является равномерным
|
|
|
|
24 |
|
|
|
|
и, следовательно, касательное ускорение точки С будет |
равно нулю, поскольку |
|||||||
равно нулю угловое ускорение: ',P Q ∙ S 0 , |
|
|
||||||
Нормальное ускорение точки С найдем по формуле |
м |
|
||||||
|
|
', ; ∙ S 100 ∙ 0,05 5 |
|
|||||
|
|
с . |
|
|||||
Поскольку модуль касательного ускорения центра масс равен нулю, то полное |
||||||||
ускорение равно нормальному ускорению. |
|
|
|
|||||
Воспользуемся теоремой о движении центра масс: |
|
|
||||||
|
|
|
, |
?в. |
|
|
|
|
Приравнивая соответствующие модули, получим, что |
|
|
||||||
|
|
|
Re = ma |
= 20 ×5 ( кг × м) = 100 (Н ). |
|
|||
|
|
|
|
C |
|
с2 |
|
|
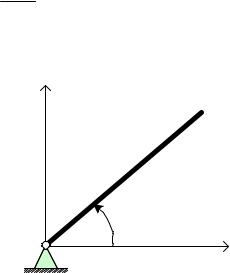
Задача 2.5. Однородный прямолинейный стержень ОА вращается вокруг |
||||||||
неподвижной оси, перпендикулярной |
|
|
y |
|
|
|||
стержню и проходящей через точку О, в |
|
A |
|
|||||
соответствии с уравнением |
φ = πt2/2 . |
|
|
|
|
|||
Установить направление главного вектора |
|
|
|
|||||
внешних сил, действующих на стержень при |
|
|
|
|||||
t = 0. |
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
ϕ |
x |
|
|
|
|
|
O |
|
||
Дифференцируя закон вращения, получим |
|
|
||||||
|
|
|
||||||
сначала выражение для угловой скорости: |
|
|
|
|||||
& |
|
|
|
|
|
|
|
|
ω = ϕ = π t, |
|
|
|
|
|
|
||
а затем угловое ускорение: |
|
|
|
|
|
|
||
& |
&& |
|
|
|
|
|
|
|
ε = ω = ϕ = π = const. |
|
|
|
|
|
|||
При t=0 кинематические параметры будут равны: |
|
|
||||||
ϕ = 0, |
|
ω = 0, |
ε = π . |
|
|
|
|
|
Видно, что при t=0 |
стержень занимает горизонтальное положение (ϕ = 0) . |
|
||||||
Найдем модуль касательного и нормального ускорений: |
|
|
||||||
|
|
|
',P Q ∙ S 9 ∙ S , |
|
|
|||
|
|
|
', ; |
∙ S 0. |
|
|
||
Поскольку модуль нормального ускорения центра масс равен нулю, то полное |
||||||||
ускорение равно касательному ускорению. |
|
|
|
|||||
Из теоремы о движении центра масс |
, ?в |
|
|
|||||
следует, что главный вектор внешних сил направлен в том же направлении, что |
||||||||
и полное ускорение, то есть вертикально вверх (перпендикулярно отрезку ОС в |
||||||||
положительном направлении вращения). |
|
|
|
|||||
25 |
|
|
|
|
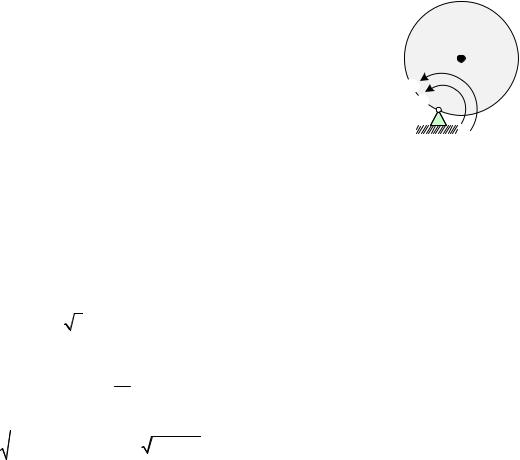
Задача 2.6. Однородный диск радиуса r = 0.2 м и массы |
|
|
|
|
М = 30 кг вращается вокруг неподвижной оси, |
|
|
|
C |
перпендикулярной плоскости диска и отстоящей от его центра |
|
|
|
|
С на расстояние ОС = r. |
ω ε |
|
|
|
Определить модуль главного вектора внешних сил, |
O |
|||
действующих на диск в момент времени, когда угловая скорость |
|
|
|
|
диска ω = 1 рад/с, а его угловое ускорение ε = 4√5 рад/с2. |
|
|
|
|
Решение.
В данной задаче однородный диск вращается относительно оси О, перпендикулярной плоскости диска. Центр масс находится в точке С, которая движется по окружности.
При этом касательное ускорение точки С направлено перпендикулярно отрезку ОС и равно
aτ |
= ε ×ОС = 4 |
|
× 0.2 ( |
м |
), |
||
5 |
|||||||
|
|||||||
С |
|
|
|
с |
2 |
|
|
|
|
|
|
|
|
||
а нормальное ускорение точки С направлено от точки С к точке О и равно
an = ω 2 ×OC = 12 × 0.2 ( м ).
С с2
Модуль полного ускорения будет равен:
a = |
(aτ |
)2 + (an |
)2 |
= 0.2 × |
|
|
= 0.2 ×9 = 1.8( |
м |
), |
|
16 ×5 +1 |
||||||||||
|
|
|||||||||
C |
C |
C |
|
|
|
|
|
с2 |
||
По теореме о движении центра масс получим значение модуля главного
вектора внешних сил:
Vв ', 30 ∙ 1.8 54 Y.
2.3. Теорема об изменении количества движения в дифференциальной форме
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость: Z C. Её также называют импульсом материальной точки.
Количеством движения механической системы называется геометрическая сумма количеств движения всех точек системы:
Z @ [C[.
[B
Поскольку ∑ [C[ C, то Z C,
[B , .
26
Количество движения характеризует только поступательную часть движения и никакого отношения не имеет к его вращательной составляющей.
Теорема
Производная по времени от количества движения механической системы
равна главному вектору внешних сил, действующих на систему:
Z @ в
AB A
или в проекциях на оси декартовой системы координат:
dQ |
|
n |
|
|||
|
|
x |
|
= ∑ Fkxe |
|
|
dt |
|
|
||||
|
|
|
k =1 |
|
||
dQ |
|
|
n |
|
||
|
|
|
y |
|
= ∑ Fkye . |
(2.1) |
|
dt |
|
|
|||
|
|
|
k =1 |
|
||
dQ |
|
n |
|
|||
|
|
z |
|
= ∑ Fkze |
|
|
|
|
|
|
|||
dt |
|
|
k =1 |
|
||
2.4. Теорема об изменении количества движения в интегральной форме |
||||||
Импульсом силы за некоторый интервал времени (0,t ) |
называется величина, |
|||||
равная интегралу: |
|
|
|
|
|
|
\ . |
|
|||||
Если *EFG то \ ∙ ∆, где t − интервал времени, в течение которого действовала сила.
Теорема
Изменение количества движения механической системы за некоторый промежуток времени равно сумме импульсов действующих на систему
внешних сил за этот промежуток времени:
∆Z @ \вA
AB
или в проекциях на координатные оси
|
|
n |
|
Qx |
= ∑ Skxe |
|
|
k =1 |
|
|
n |
|
Qy |
= ∑ Skye . |
|
|
k =1 |
|
|
n |
|
Qz |
= ∑ Skze |
|
|
k =1 |
Для одной материальной точки теорема приобретает вид:
27
C C \,
где S - импульс равнодействующей всех сил, приложенных к точке.
Следствие 1.
Если главный вектор внешних сил механической системы все время равен нулю, то вектор количества движения системы не изменяется с течением времени.
То есть если ∑ в 0, то Z 0 и следовательно Z *EFG
, , [B [ , ,
или C, *EFG .
Следствие 2.
Если сумма проекций всех внешних сил механической системы на какуюлибо ось все время равна нулю, то проекция количества движения на эту ось постоянна.
n |
|
dQx |
|
|
Например, если ∑ Fixe ≡ 0, |
то из (2.1) следует, что |
≡ 0 и Qx ≡ const . |
||
|
||||
i =1 |
|
dt |
||
Задача 2.7. Механическая система состоит из двух материальных точек с |
|||
массами m 2 кг |
и |
m |
3кг, движущимися с взаимно перпендикулярными |
скоростями v 4 мс |
и |
v |
2 мс. |
Чему равно количество движения этой механической системы?
Решение.
Количество движения механической системы определяется по формуле:
Z ∑c mbCb
bB .
m2v 2 |
Q |
|
|
|
m1v 1 |
Для двух материальных точек оно равно сумме двух векторов
Z m C m C , которые можно сложить по правилу параллелограмма:
Q . |
|
|
. 2 ∙ 4 3 ∙ 2 10 кг∙мс . |
m v m v |
|
||
Задача 2.8. По горизонтальной платформе, движущейся со скоростью v0, |
|||
перемещается тележка с |
относительной скоростью u0. Найти скорость |
||
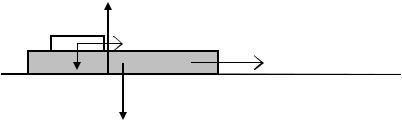
28
платформы при торможении тележки, если их массы равны M и m соответственно.
Решение.
На систему, состоящую из платформы весом P = Mg и тележки весом p = mg, помимо этих двух сил действует реакция дорожного полотна N, приложенная к основанию платформы (рис. 8).
N
v0 + u0
v0 |
x |
|
p
P
Рис.8
Главный вектор внешних сил системы: R = P + p + N перпендикулярен оси Ox, поэтому Rx(e) = 0 и справедливо следствие из теоремы об изменении количества движения системы:
dQx/dt = Rx(e)
или Qx0 = Qxt .
В начальный момент времени абсолютная скорость тележки складывается из переносной, равной скорости платформы, и относительной – u0 , поэтому при t = 0 количество движения системы равно:
Qx0 = Mv0 + m(v0 + u0). |
(1) |
В момент времени t , соответствующий окончанию торможения тележки, количество движения системы равно:
Qxt = (M + m)v, |
(2) |
где v – искомая скорость платформы. Приравнивая (1) и (2), получим:
v = [Mv0 + m(v0 + u0)]/(M + m) = v0 + mu0/(M + m).
29
2.5. Теорема об изменении кинетического момента
Теоремы о движении центра масс и об изменении количества движения описывают только поступательную часть движения твердого тела. Вращательную часть движения описывает теорема об изменении кинетического момента.
Моментом количества движения материальной точки относительно некоторого центра называется векторное произведение
e f C ,
где r – радиус вектор точки, v – скорость.
Направление вектора момента количества движения определяется по правилу правого винта.
Кинетическим моментом механической системы относительно некоторого центра О называется сумма моментов количеств движения всех точек данной системы относительного этого центра:
ii
g @ eh |
@ f [C . |
Bj |
Bj |
Если механическая система представляет собой твердое тело, то кинетический момент должен определяться не суммированием, а путем интегрирования по объему.
Если точка О является началом системы координат, то проекции кинетического момента на оси будут являться кинетическими моментами механической системы относительно осей:
( KO )x = Kx
( KO )y = Ky
( ) =
KO z Kz
Чтобы вычислить момент количества движения относительно оси надо: спроектировать вектор mC на плоскость перпендикулярную оси, величину этой проекции умножить на ее плечо относительно точки пересечения оси с плоскостью, добавить знак в зависимости от направления вектора.
Кинетический момент вращающегося тела
