5897
.pdf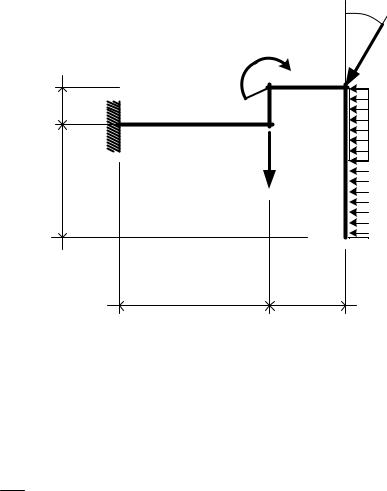
|
20 |
|
|
|
α |
|
М |
P |
1 м |
А |
q |
|
|
F |
3 м |
|
|
|
4 м |
2 м |
|
Рис. 1.24 |
|
Решение:
1.Отбрасываем связи (опоры) и заменяем их неизвестными реакциями. Распределенные нагрузки заменяем равнодействующими (рис.1.25).
2.Раскладываем наклонные силы на составляющие по осям х и у (рис.1.25).
3.Заменяем распределенную нагрузку ее равнодействующей:
Q= q × 4м = 3 кН × 4м = 12кН
м.
4.Составляем уравнения равновесия.
∑ X i = 0 |
|
X A - P ×sinα - Q = 0 |
|||
|
|
= 0 |
|
|
|
|
Y |
|
|
- F - P × cosα = 0 |
|
∑ i |
R |
YA |
|||
∑M A (Fi ) = 0 |
M A - M - F × 4 - Q ×1 - P × cosα × 6 + P ×sinα ×1 = 0 |
||||
|
|
|
|
|
|
|
|
21 |
|
|
y |
|
P |
|
|
α |
|
|
M A |
|
|
|
М |
|
|
X A |
А |
|
В |
|
|
F |
x |
|
|
Q |
|
|
YA |
|
|
|
|
q |
|
|
RA |
|
|
|
|
|
|
|
|
|
С |
|
|
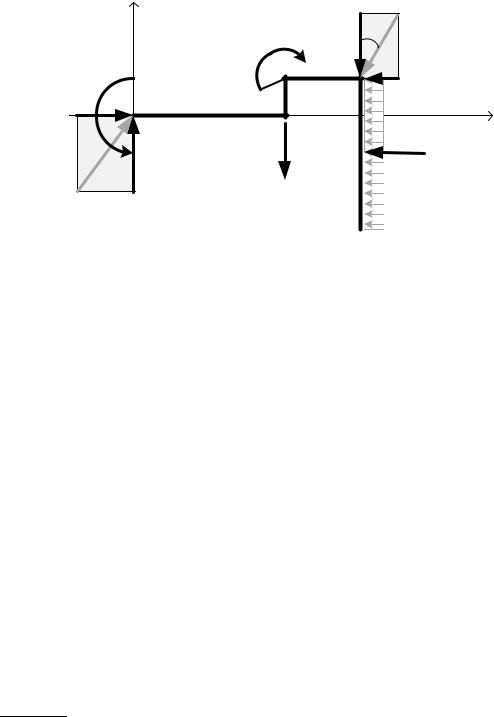
Рис. 1.25 |
|
5. Решаем систему уравнений и находим неизвестные реакции:
∙ кН,
∙ √ ∙ , , кН,∙ ∙ ∙ √ ∙ ∙ ∙
∙ ∙ ∙ , ∙ ∙ , ∙ , кНм
6.Выполняем проверку, вычисляя сумму моментов относительно произвольной точки С.
R |
) = MA - M - XA ×3 -YA × 6 + F × 2 |
+ P ×sinα × 4 + Q × 2 |
|
∑M Ñ (Fi |
= |
||
|
= 96.96 - 6 -17 ×3 -16.66 × 6 + 8 |
× 2 +10 × 0.5 × 4 +12 × |
2 = 0.0 |
Проверка выполняется с удовлетворительной точностью.
Ответ: Реакции равны: кН, , кН, , кНм,
, , кН
.
Задача 1.13. Равновесие произвольной плоской системы сил Дано: F=8кН, Р=5кН, q=4кН/м.
Определить реакции связей.
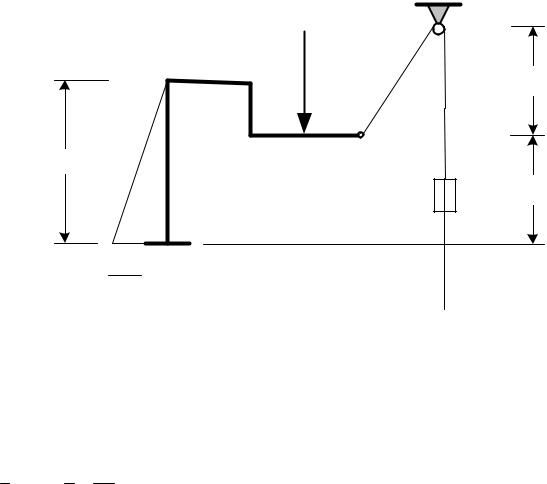
22
6м
q = 4 кН
м
Решение
|
F = 8кН |
D |
4м |
|
|
B |
C |
|
4м |
A |
P = 5кН |
3м
2м
2м
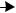
3м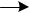
Рис. 1.26
1.Отбрасываем связи (опоры) и заменяем их неизвестными реакциями. Распределенные нагрузки заменяем равнодействующими.
2.Раскладываем наклонные силы на составляющие по осям х и у.
3.Заменяем распределенную нагрузку ее равнодействующей:
Q = 1 q × 6 м = 1 × 4 кН ×6м = 12кН
|
|
2 |
2 м |
. |
4. Составляем уравнения равновесия. |
||||
∑ |
|
|
|
|
|
|
mA = 0 |
-Q × 2 - F ×5 + P cosα ×7 - P sin α × 4 + M A = 0, |
|
|
∑ X = 0 |
Q + X A + P sin α = 0, |
||
|
∑Y = 0; |
|
- F + P cosα = 0. |
|
|
YA |
|||
5. Решаем систему уравнений и находим неизвестные реакции, учитывая, что sinα = 0.6, cosα = 0.8. .
M A = +Q ×2 + F ×5 - P cosα ×7 + P sinα ×4 =
= +12 × 2 + 8×5 - 5×0.8×7 + 5×0.6 ×4 = 24 + 40 - 28 +12 = 48кНм,
X A = -Q - P sinα = -12 - 5×0.6 = -15кН (направление противоположное),
YA = +F - P cosα = 8 - 5×0.8 = 4кН.
|
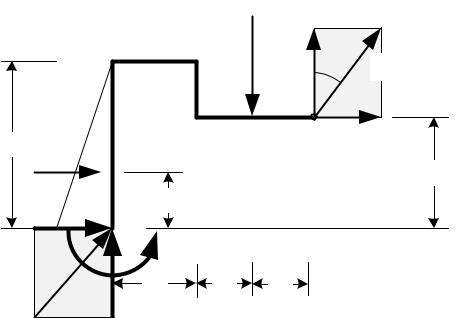
23 |
|
|
|
|
F = 8кН |
P cosα |
|
|
|
D |
|
α |
P = 5кН |
|
|
|
|
|
Q |
B |
C |
P sin α |
|
|
||||
|
A |
|
|
|
X A |
M A |
|
|
|
RA |
YA |
|
|
|
Рис. 1.27 6.Выполняем проверку, вычисляя сумму моментов относительно произвольной
точки D.
∑ M D = M A -YA ×3 + X A ×6 + Q × 4 - F × 2 + P cosα × 4 + P sin α × 2 =
=48 - 4 ×3 + (-15)×6 +12 × 4 - 8 × 2 + 5 ×0.8 × 4 + 5 ×0.6 × 2 =
=48 -12 - 90 + 48 -16 +16 + 6 = 0.
Проверка выполняется. Ответ: Реакции равны:
M A = 48кНм, X A = -15кН (направление противоположное), YA = 4кН.
1.3 Равновесие плоской системы тел
Задача 1.14. Равновесие системы тел на плоскости Дано: F, q, M.
Определить реакции опор А, D, E и G.
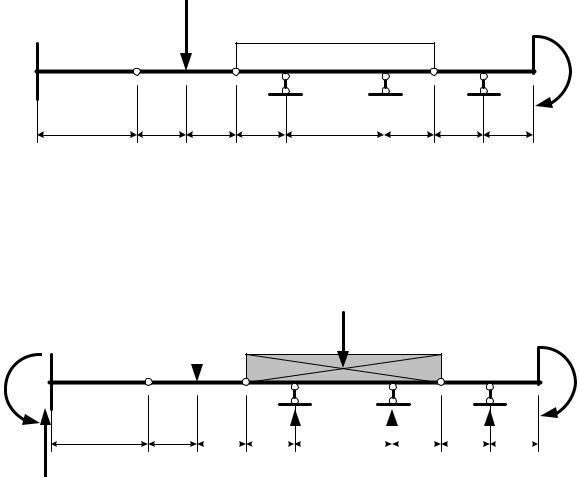
24
F q M
A |
B |
|
C |
|
D |
E |
F |
G |
|
2a |
a |
a |
a |
2a |
a |
a |
a |
Рис. 1.28
Решение:
1.Отбрасываем связи (опоры) и заменяем их неизвестными реакциями (рис.1.29).
2.Заменяем распределенную нагрузку ее равнодействующей: .
M A |
F |
Q = 4qa |
M |
|
|||
|
|
|
|
A B
2a a
R
RA
C |
D |
E |
F |
G |
a |
|
a |
|
2a |
|
|
a |
|
a |
|
|
a |
||
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
RG |
|
|
|
|
|
D |
|
|
|
E |
|
|
|
|
|
Рис. 1.29
3. Составляем первое дополнительное уравнение, выражающее отсутствие поворота диска FG относительно диска AF (рис.1.30):
n |
|
|
|
|
∑ МFправ = 0, |
−М + RG a = 0, |
|||
i=1 |
|
|
|
|
R = |
M |
= |
qa2 |
= qa. |
|
|
|||
G |
a a |
|
||
|
|
|||
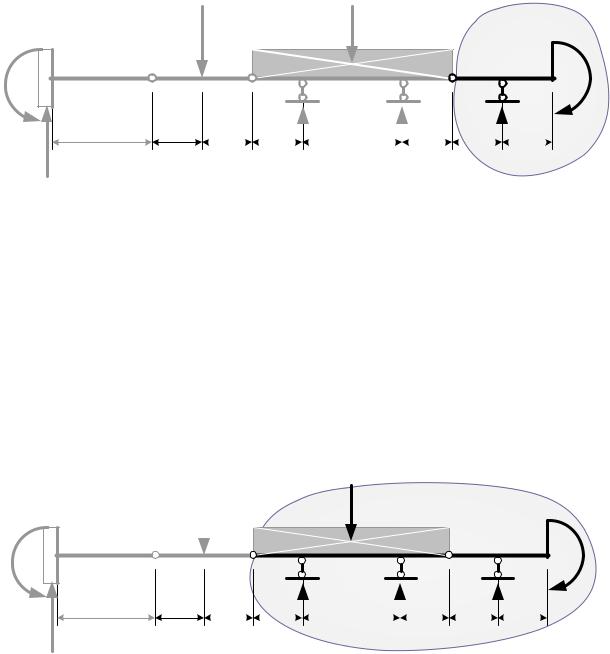
25
M A |
F |
Q = 4qa |
M |
|
A B
2a a
R
RA
C |
D |
E |
F |
G |
a |
|
a |
|
2a |
|
|
a |
|
a |
|
|
a |
||
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
RG |
|
|
|
|
|
D |
|
|
|
E |
|
|
|
|
|
Рис. 1.30
4. Составляем дополнительное уравнение, выражающее отсутствие поворота диска СG относительно диска AС (рис.1.31):
n |
|
|
|
= 0, |
|
|
|
|
|
|
|
|
∑ МCправ |
-M |
+ RG |
×5a + RE |
×3a + RD ×a -Q ×2a = 0, |
|
|||||||
i=1 |
|
|
|
|
|
|||||||
3R |
|
+ R |
|
= −5R + 2Q + |
M |
, |
|
|
|
|
|
|
E |
D |
|
|
|
|
|
|
|
||||
|
|
G |
a |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
3R + R = -5qa + 2 × 4qa + |
qa2 |
, |
|
|
|
|||||||
|
|
|
|
|||||||||
E |
D |
|
|
|
a |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
3RE + RD = 4qa. |
|
|
|
|
|
|
|
|
||||
|
|
M A |
|
|
|
|
|
F |
Q = 4qa |
M |
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A B
2a a
R
RA
C |
D |
E |
F |
G |
a |
|
a |
|
2a |
|
|
a |
|
a |
|
|
a |
||
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
RG |
|
|
|
|
|
D |
|
|
|
E |
|
|
|
|
|
Рис. 1.31
5. Составляем дополнительное уравнение, выражающее отсутствие поворота диска ВG относительно диска AB (рис.1.32):
n |
|
|
|
|
∑ МBправ = 0, |
|
-M + RG ×7a + RE ×5a + RD ×3a -Q ×4a - F ×a = 0, |
||
i=1 |
|
|
||
5R + 3R = −7R + 4Q + |
M |
+ F , |
||
|
||||
E |
D |
G |
a |
|
|
|
|
||
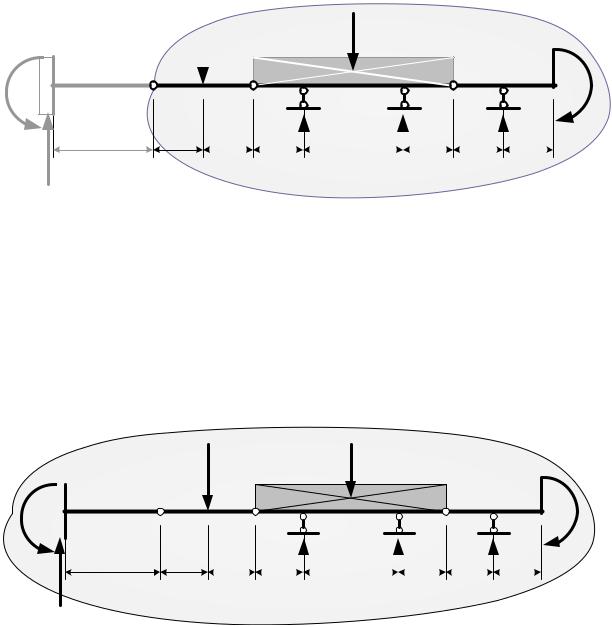
26
5R + 3R = -7qa + 4 × 4qa + |
qa2 |
+ qa, |
|
|
||
|
|
|
||||
E |
D |
a |
|
|
|
|
|
|
|
|
|
|
|
5RE + 3RD =11qa. |
|
|
|
|
|
|
|
M A |
|
|
F |
Q = 4qa |
M |
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|
|
|
A B
2a a
R
RA
C |
D |
E |
F |
G |
a |
|
a |
|
2a |
|
|
a |
|
a |
|
|
a |
||
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
RG |
|
|
|
|
|
D |
|
|
|
E |
|
|
|
|
|
Рис. 1.32
6. Решаем систему уравнений, полученных в пунктах 4 и 5:
RD = 4qa -3RE .
5RE + 3(4qa − 3RE ) = 11qa.
-4RE +12qa =11qa.
RE = 0.25qa.
RD = 4qa - 0.75qa = 2.25qa.
M A |
F |
Q = 4qa |
M |
|
A B
2a a
R
RA
C |
D |
E |
F |
G |
a |
|
a |
|
2a |
|
|
a |
|
a |
|
|
a |
||
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
RG |
|
|
|
|
|
D |
|
|
|
E |
|
|
|
|
|
Рис. 1.33
7. Пользуясь аксиомой отвердения, составляем уравнения равновесия всей конструкции, считая ее абсолютно твердым телом (рис. 1.33).
n |
|
|
∑ МA |
= 0, |
- M + RG ×9a + RE ×7a + RD ×5a -Q ×6a - F ×3a = 0, |
i=1 |
M A |
M A = +M - RG ×9a - RE ×7a - RD ×5a + Q ×6a + F ×3a,
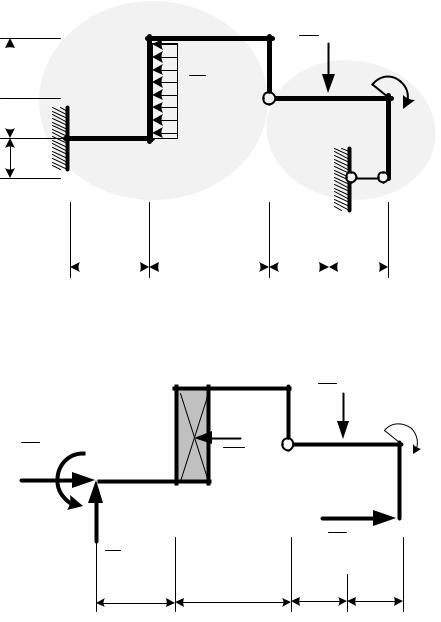
27
M A = +qa2 - qa ×9a - 0.25qa ×7a - 2.25qa ×5a + 4qa ×6a + qa ×3a = 6qa2 .
n |
|
|
|
|
∑Yi |
= 0, |
+ RD |
+ RE |
+ RG − F − Q = 0, |
i=1 |
RA |
RA = −2.25qa − 0.25qa − qa + qa + 4qa = 1.5qa.
Ответ: Реакции равны: M A = 6qa2 , RA = 1.5qa, RD = 2.25qa, RE = 0.25qa, RG = qa.
Задача 1.15. Равновесие системы тел на плоскости Дано: F = 24 кН , q = 10кН / м, M = 30кНм . Определить реакции опор А и В.
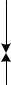1м 1м 1.5м
|
D |
|
|
F |
М |
|
q |
|
A |
C |
|
B
2м |
|
3м |
|
1.5м |
1.5м |
||
|
|
|
|
|
|
|
|
Рис. 1.34
Решение.
М
C
Рис. 1.35
28
1.Отбрасываем связи (опоры) и заменяем их неизвестными реакциями.
2.Заменяем распределенную нагрузку ее равнодействующей
Q= q ×1.6м = 10 кН ×1.6м = 16кН
м.
3.Составляем уравнение, выражающее отсутствие поворота второго диска относительно первого диска.
∑ mC(2) = 0; |
- F ×1.5 - M + X B × 2 = 0; |
||||||
|
X B |
= |
F ×1.5 |
+ M |
= |
24 ×1.5 + 30 |
= 33кН. |
откуда |
|
|
|
||||
|
2 |
2 |
|
||||
4. Пользуясь аксиомой отвердения, составляем уравнения равновесия всей конструкции, считая ее абсолютно твердым телом.
∑ X = 0 |
X A + X B - Q = 0 |
|
|
|
|
|
|
|
|
∑Y = 0 |
YA - F = 0 |
|
|
|
|
|
- F × 6.5 |
- M + X B |
×1 = 0. |
∑ mA = 0; |
M A + Q ×1.25 |
|||
5. Решаем систему уравнений и находим неизвестные реакции.
X A = -X B + Q = -33 + 25 = -8кН;
YA = F = 24кН;
M A = -Q ×1.25 + F × 6.5 + M - X B ×1 = -25×1.25 + 24 × 6.5 + 30 - 33×1 = 121.75кН × м.
6. Выполняем проверку, вычисляя сумму моментов всех сил приложенных к раме относительно произвольной точки D.
∑ mD = M A + X A × 2.5 - YA × 5 - Q ×1.25 - F ×1.5 - M + X B × 2 =
121.75 - 8 × 2.5 - 24 ×5 - 25×1.25 - 24 ×1.5 - 30 + 33×3.5 = 0
Проверка выполняется.
Ответ: Реакции равны: X A = -8кН |
(сила направленав другуюсторону), |
YA = 24кН, M A = 121.75кН × м, |
X B = 33кН. |
1.4 Равновесие пространственной системы произвольно расположенных сил
Условием равновесия произвольной пространственной системы сил является равенство нулю главного вектора и главного момента. Для этого необходимо, чтобы суммы проекций сил на каждую из координатных осей и суммы моментов сил относительно каждой из координатных осей были равны нулю:
n |
n |
n |
n |
R |
n |
R |
n |
R |
∑Fix = 0, |
∑Fiy = 0, |
∑Fiz = 0, |
∑Mx (Fi ) = 0, |
∑M y (Fi ) = 0, |
∑M z (Fi ) = 0. |
|||
i=1 |
i=1 |
i=1 |
i=1 |
|
i=1 |
|
i=1 |
|
29
Таким образом, в статике для произвольной пространственной системы сил в общем случае можно составить шесть уравнений равновесия.
Задача 1.16
Дано: |
F = 8кН; Р =12кН; q = 2кН / м. |
|
|
|
|
|
|
|||||||
Определить реакции связей. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
F |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1м
2м
P
2м 2м
Рис.1.36
Решение:
z |
Q |
|
w X C |
|
F |
|
|
|
|
|
|
|
C v |
|
|
|
|
u |
|
Y A A |
|
|
y |
|
|
|
|
B |
|
X A |
P |
X B |
|
|
Z A |
Z B |
|||
|
||||
x |
|
|
|
|
|
Рис. 1.37 |
|
||