
5818
.pdf
Пусть |
функция y = f (x) дифференцируема в интервале (a; b) и |
x0 (a;b). |
Точку (x0 ; f (x0 )) графика функции y = f (x) называют точкой |
перегиба этого графика, если существует такая ε – окрестность точки x0 оси
Ox , в границах которой график функции y = f (x) слева и справа от точки x0 имеет разные направления выпуклости (cм. рис. 5).
y
a x0 −ε 0 x0 x0 +ε b |
x |
Рис. 5 |
|
Теорема. (Необходимое условие перегиба функции). Если x0 – точка перегиба функции y = f (x), то вторая производная функции в этой точке
либо равна нулю, либо не существует.
Теорема. (Достаточное условие перегиба функции). Если функция
y = f (x) |
|
непрерывна в ε – окрестности точки |
x0 , имеет |
в |
точке |
x0 |
|
конечную |
или бесконечную определенного знака производную |
f |
′′ |
а |
|||
(x0 ), |
|||||||
функция |
f |
′′ |
x0 , кроме, |
быть может |
|||
(x) определена в ε – окрестности точки |
|||||||
самой точки x0 , и меняет знак при переходе через эту точку, то |
x0 |
– точка |
|||||
перегиба функции
20

Пример 1. Найти интервалы выпуклости (вогнутости) и точки
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перегиба функции |
y = |
9 × 3 |
х11 |
|
- |
9 × 3 х5 |
. |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
88 |
|
10 |
|
|
|
|
|
|
|
|||||||||||
|
Решение. Область определения D данной функции есть множество |
|||||||||||||||||||||||||||||||||
всех действительных чисел R , то есть D = R . |
||||||||||||||||||||||||||||||||||
|
Находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
8 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y'= |
9 |
× |
11 |
× x |
|
- |
|
9 |
× |
5 |
|
× x |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
88 |
3 |
|
|
|
|
3 |
|
= 3 |
|
|
− 1 = |
|
|
|
|
− 1 . |
||||||||||||||||||
y′′ = (y′)′ = x 3 |
|
− x |
3 |
x5 |
x |
|
||||||||||||||||||||||||||||
|
|
5 |
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x |
|
|
|
3 x |
||||||||
Используя необходимое условие перегиба, находим:
y′′ = 0 x 2 −1 = 0 , откуда x = ±1 ,
y′′ не существует, если 3  х = 0 , откуда x = 0 .
х = 0 , откуда x = 0 .
Используем достаточные условия перегиба:
Отметим точки x = ±1, x = 0 на области D и определим знаки y′′
слева и справа от каждой точки.
y ' |
|
+ |
– |
+ |
- |
|
|||
y |
-1 |
0 |
1 |
x |
Так как x = 0 D и при переходе через эту точку |
y′′ меняет знак, то |
x = 0 – точка перегиба данной функции. Аналогично, |
точки x = ±1 тоже |
являются точками перегиба графика функции. |
|
График функции выпуклый вниз на интервалах (−1; 0), (1; + ∞) .
График функции выпуклый вверх на интервалах (− ∞; 0), (0;1).
21

Пример 2. Найти интервалы выпуклости (вогнутости) и точки
перегиба функции y = х × 
 4 - х2 .
4 - х2 .
Решение. Найдем область определения D данной функции:
4 - х2 ³ 0 -2 £ х £ 2 .
Находим:
y'=1× |
|
|
+ х× |
|
- 2х |
|
= |
4 |
|
- 2х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4 - х2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
4 - х2 ; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 4 - х2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2х |
|
|
|
|
|
|
|
||||||
|
|
- 4х× |
4 - х |
2 |
- (4 - 2 |
х |
2 |
) × |
|
|
|
2х× (х2 - 6) |
|
||||||||||||||||||||||
y¢¢ = (y¢)¢ = |
|
|
|
2 |
|
|
|
|
|
= |
|
||||||||||||||||||||||||
|
|
|
4 - х2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
4 - х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4 - х2 )3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y¢¢ = 0 Û 2х(x2 - 6) = 0 , откуда x = 0 D , x = ± |
|
Ï D |
|||||||||||||||||||||||||||||||||
6 |
|||||||||||||||||||||||||||||||||||
y′′ не существует, если |
|
|
|
|
|
|
|
= 0 x = ±2 Î D . |
|||||||||||||||||||||||||||
|
|
(4 - х2 )3 |
|||||||||||||||||||||||||||||||||
Используем достаточные условия перегиба: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Отметим точки x = ±2, x = 0 на области |
D и определим знаки y′′ |
||||||||||||||||||||||||||||||||||
слева и справа от каждой точки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
y′′ |
-2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2 |
|
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка x = 0 является точкой перегиба графика функции.
График функции выпуклый вниз на интервале (− 2; 0).
График функции выпуклый вверх на интервале (0;2) .
3) Асимптоты графика функции
Прямую L называют асимптотой графика функции y = f (x), если расстояние d от точки M (x; y) кривой y = f (x) до прямой L стремится к
нулю при неограниченном удалении этой точки по кривой от начала
координат (см. рис. 6).
22
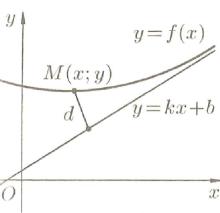
Рис. 6
Различают вертикальные и наклонные асимптоты.
Прямая x = х0 является вертикальной асимптотой кривой y = f (x),
если хотя бы один из односторонних пределов функции |
y = f (x) в точке |
|||||
x = х равен бесконечности, то есть |
lim f (x) = ±∞ или |
lim f (x) = ±∞ . |
||||
0 |
|
|
|
x→х0 −0 |
x→х0 +0 |
|
Как правило, точки х0 находятся среди точек разрыва второго рода. |
||||||
Прямая y = kx + b является наклонной асимптотой кривой y = f (x), |
||||||
если одновременно существуют конечные пределы: |
|
|||||
k = lim |
f (x) |
|
b = lim ( f (x)− kx) |
. |
||
|
|
и |
||||
x→±∞ |
x |
x→±∞ |
||||
|
|
|||||
Если же хотя бы один из вышеприведенных пределов не существует или равен бесконечности, то наклонных асимптот график функции не имеет.
В случае, когда k = 0 , наклонная асимптота y = b становится
горизонтальной асимптотой кривой y = f (x).
23

3
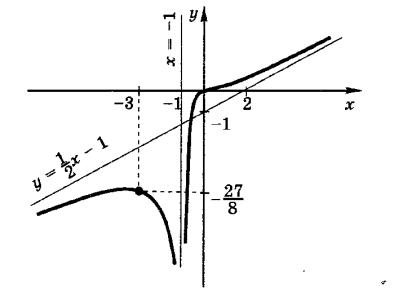
Пример 1. Найти асимптоты кривой y = x+ 2 .
2(x 1)
Решение. Данная функция определена в интервалах (− ∞; −1) и
(− 1;+∞).
Рассмотрим граничную точку области определения x = −1. Поскольку
|
x3 |
|
|
− 1 |
|
|
|
lim |
|
|
= |
|
|
= −∞ , то прямая x = −1 |
есть вертикальная |
|
2 |
|
|||||
x→−1−0 2(x + 1) |
|
|
+ 0 |
|
|
||
асимптота данной кривой.
Наклонные асимптоты находим в виде уравнения прямой y = kx + b :
|
|
f (x) |
|
|
|
x3 |
|
∞ |
|
|
|
x3 |
|
|
|
|
||||
k = lim |
|
|
|
= |
lim |
|
= |
|
= lim |
|
|
|
|
|
|
|
= |
|||
x |
|
|
2 |
|
|
|
|
1 |
2 |
|||||||||||
x→±∞ |
|
|
|
x→±∞ 2(x + 1) |
x |
|
∞ |
x→±∞ |
3 |
+ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2х |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
= lim |
|
|
1 |
|
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
x → ±∞ |
+ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b = lim ( f (x)- kx) = |
|
|
x |
3 |
- 1 |
|
lim - 2x |
2 |
- x = -1 |
|
|||||||
|
lim |
|
× x = |
|
. |
||||||||||||
|
|
|
|
||||||||||||||
x→±∞ |
|
|
|
|
|
x→±∞ 2(x +1)2 |
2 |
|
x→±∞ 2(x +1)2 |
||||||||
Следовательно, существует наклонная асимптота |
y = |
1 |
x − 1 |
. Таким образом, |
|||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
кривая y = |
x3 |
|
имеет одну вертикальную асимптоту |
x = −1 и одну |
|||||||||||||
2(x + 1)2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
наклонную |
y = |
1 |
x − 1 |
(см. рис. 7). |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
24
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7 |
|
|
|
|
|
|
|
|
|
|
|
||
|
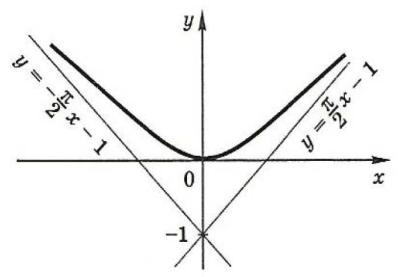
Пример 2. Найти асимптоты кривой y = x × arctgx . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Решение. Данная функция определена и непрерывна на всей числовой |
|||||||||||||||||||||||||||||||||||||||
прямой, следовательно, вертикальных асимптот эта кривая не имеет. |
|
|||||||||||||||||||||||||||||||||||||||
|
Найдем наклонные асимптоты этой кривой: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
k1 |
= lim |
|
f (x) |
= lim |
|
x × arctgx |
= lim arctgx = π , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x→+∞ x |
|
x→+∞ |
|
|
|
x |
|
|
|
x→+∞ |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
b1 |
= lim |
( f (x) |
|
|
|
|
|
|
|
|
× arctgx - |
π |
|
|
= lim x × |
|
|
|
|
|
|
|
π |
|
||||||||||||||||
- kx) = lim x |
|
|
|
× x |
arctgx - |
2 |
= [¥ × 0]= |
|||||||||||||||||||||||||||||||||
|
x→+∞ |
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
2 |
|
|
x→+∞ |
|
|
|
|
|
|
|
|
||||||||||||
|
|
arctgx − |
π |
|
|
|
|
|
|
|
(arctgx − |
π |
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
+1 |
|
|
|
|||||||||||||||||||||
= lim |
2 |
= |
0 |
|
= lim |
2 )' |
= lim |
|
|
|
= |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
x→+∞ |
|
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
( |
1 )' |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
(−x2 )' |
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
lim |
− x2 |
= |
∞ |
= |
lim |
|
|
|
|
= |
lim |
− 2x |
= −1, |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
+ x |
2 |
)' |
|
|
|||||||||||||||||||||||||||
|
+ x |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
x→+∞ 1 |
|
|
|
|
∞ |
|
|
x |
→+∞ (1 |
|
|
x→+∞ |
2x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
следовательно, |
|
y = π |
|
× x -1 наклонная |
|
|
асимптота кривой |
|
y = x × arctgx |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при x → +∞ .
25
k2 |
= lim |
|
f (x) |
= lim |
|
x × arctgx |
= lim arctgx = - π , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x→−∞ |
x |
|
x→−∞ |
|
|
x |
|
|
|
x→−∞ |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
b2 |
= lim |
( f (x) - kx) = |
|
|
|
× arctgx |
+ |
π |
|
|
|
|
|
|
+ |
π |
|
= [¥ × 0] = |
||||||||||||||||||||||||
lim x |
2 |
× x = lim x × |
arctgx |
2 |
|
|||||||||||||||||||||||||||||||||||||
|
x→−∞ |
|
|
|
|
|
|
|
|
|
x→−∞ |
|
|
|
|
|
|
|
|
|
x→−∞ |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
arctgx + 2 |
|
|
|
|
|
|
(arctgx + |
2 )' |
|
|
|
|
|
|
|
= |
|
|
|
|
|||||||||||||||||||||
= lim |
= |
|
0 |
|
= lim |
= lim |
|
x2 + 1 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
x→−∞ |
|
|
1 |
|
|
|
|
|
x→−∞ |
|
|
1 |
|
|
|
|
x→−∞ |
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
( |
)' |
|
|
|
|
|
− |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
− x2 |
|
∞ |
|
|
|
|
|
|
|
(−x2 )' |
= |
|
|
|
− 2x = −1, |
|
|
|
|
|
|||||||||||||||||||
= |
lim |
|
|
|
|
|
|
= |
|
|
= |
lim |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
+ x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x→−∞ 1 |
|
|
|
∞ |
|
|
|
x→−∞ (1 + x |
|
)' |
|
|
x→−∞ |
2x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
следовательно, y = - π × x -1 наклонная асимптота кривой |
y = x × arctgx |
|
при |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x → −∞ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Таким |
|
|
образом, |
|
|
график |
|
функции |
|
y = x × arctgx |
имеет |
только |
две |
||||||||||||||||||||||||||||
наклонные |
|
|
|
асимптоты |
|
y = π × x -1 |
|
при |
|
x ® +¥ и |
y = - π × x -1 |
|
при |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
x → −∞ (см. рис. 8).
Рис. 8
26

Общая схема исследования функции и построения графика
1.Найти область определения функции.
2.Исследовать функцию на непрерывность, указать промежутки непрерывности функции.
3.Найти нули функции и интервалы знакопостоянства, а также точку пересечения с осьюOy .
4.Исследовать функцию на симметрию и периодичность.
5.Найти асимптоты.
6.Исследовать функцию на монотонность и точки экстремума.
7.Указать интервалы выпуклости (вогнутости) и точки перегиба функции.
8.Если этой информации недостаточно, то дополнительно найти некоторые точки графика.
9.Построить график функции.
Рассмотрим примеры исследования функции и построения её графика.
Пример 1. Провести |
|
|
|
y = |
x 3 |
|||||
полное |
исследование функции |
|
|
и |
||||||
x 2 |
|
|||||||||
|
|
|
|
|
|
|
− 3 |
|||
построить её график. |
|
|
|
|
|
|
|
|||
Исследование |
|
|
|
|
|
|
|
|||
1. Областью определения D данной функции y является вся числовая |
||||||||||
ось R , кроме точек x1 = |
|
|
и x2 = − |
|
(в которых знаменатель обращается |
|||||
3 |
||||||||||
|
3 |
|||||||||
в0), то есть D = R \ {± 
 3 }.
3 }.
2.Исследуем функцию на непрерывность. Данная функция является элементарной, следовательно, она непрерывна в своей области определения.
3.Чтобы определить точки пересечения графика с осью ординат,
полагаем x =0, тогда y =0. Значит кривая пересекает ось Oy в точке O(0,0) .
Эта же точка является точкой пересечения с осью Ox , так как при y = 0
27

получаем, что x = 0. |
Находим интервалы |
знакопостоянства функции |
||||||||||
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x) > 0 |
|
|
> 0 − 3 < x < 0, x > 3. |
|
|
|||||||
|
x2 −3 |
|
|
|||||||||
|
f (x) < 0 |
x < − |
|
|
|
|
||||||
Аналогично |
3, 0 < x < |
3 . |
||||||||||
4. Функция непериодическая; исследуем ее на четность и нечетность.
Данная функция является нечетной, так как область определения
симметрична относительно начала координат и для любого x из области
определения y(−x) = |
(−x)3 |
= |
−x3 |
= −y(x). Следовательно, график ее |
|
(−x)2 −3 |
x2 −3 |
|
|||
симметричен относительно начала координат.
5.Асимптоты
a)Находим вертикальные асимптоты. Рассмотрим граничные точки области
определения x1 = 
 3 и x2 = −
3 и x2 = −
 3 . Поскольку
3 . Поскольку
|
|
|
|
x3 |
|
|
|
|
|
|
x3 |
|||||
lim |
|
|
|
|
|
= −∞, |
lim |
|
|
|
= +∞, |
|||||
|
|
|
|
|
|
|
|
|||||||||
x→− |
|
−0 x2 |
− 3 |
|
x→− |
|
+0 x2 − 3 |
|||||||||
3 |
|
3 |
||||||||||||||
|
|
|
|
x3 |
|
|
|
|
|
x3 |
||||||
lim |
|
|
|
|
= −∞, |
lim |
|
|
= +∞, |
|||||||
|
− 3 |
|
|
|||||||||||||
x→ 3 −0 x2 |
|
x→ 3 +0 x2 |
− 3 |
|||||||||||||
то прямые x = − 
 3, x =
3, x = 
 3 являются вертикальными асимптотами графика функции.
3 являются вертикальными асимптотами графика функции.
b) Выясним наличие наклонных и горизонтальных асимптот:
|
|
|
|
x3 |
|
x2 |
|
|
|
|
||||
|
y |
= lim |
|
|
|
= lim |
|
|
|
|||||
k = lim |
x2 − 3 |
= 1 ( k = 1 при x → + ∞ и при x → − ∞ ), |
||||||||||||
|
|
|
|
|
|
|
||||||||
x→∞ x x→∞ |
x |
x→∞ x2 − 3 |
|
|
|
|
||||||||
b = lim ( y − kx) = lim ( |
x3 |
|
− x) = lim |
3x |
|
= 0. |
||||||||
|
|
|
||||||||||||
x→∞ |
x→∞ |
x2 − 3 |
x→∞ x2 − 3 |
|
||||||||||
Значит, прямая y = x |
является наклонной асимптотой и при x → + ∞ и при |
|||||||||||||
x → − ∞ . Горизонтальных асимптот график не имеет.
6. Найдем интервалы монотонности и экстремумы функции, исследуя первую производную
28
/ |
|
x3 |
/ |
|
3x2 (x2 - 3) - 2x × x3 |
|
x2 (x2 - 9) |
|||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
2 . |
|
|
|||||
y = |
- 3 |
|
(x |
- 3) |
|
(x |
- 3) |
|
|
|||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x1 = − |
|
|
|
|
|
||||||||||||||||
Первая производная не существует в точках |
|
3, x2 = 3 (т.е. в |
||||||||||||||||||||
точках, в которых не существует и сама функция) и обращается в нуль, когда x2 (x2 − 9) = 0, откуда x3 = −3, x4 = 0, x5 = 3. Все полученные точки разбивают числовую ось на шесть интервалов, в которых производная не меняет знак.
Поэтому, выбирая в каждом из полученных интервалов произвольную точку,
определяем знак производной в них.
Видим, что на интервалах (−3, − 
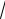 3), (−
3), (−
 3,
3, 
 3), (
3), (
 3, 3) первая
3, 3) первая
производная отрицательна, следовательно, здесь функция убывает; на
интервалах (−∞, − 3), (3, + ∞) первая |
производная |
положительна и данная |
|||||||||||
функция возрастает. При переходе через точку |
x = −3 |
первая производная |
|||||||||||
меняет свой знак с плюса на минус, поэтому |
x = −3 является точкой |
||||||||||||
максимума, а при переходе через точку |
x = 3 |
первая производная меняет |
|||||||||||
свой знак с минуса на плюс, поэтому |
x = 3 – |
точка минимума. |
Вычислим |
||||||||||
значения функции в этих точках: y(3) = |
33 |
|
= |
9 |
, |
y(−3) = |
|
(−3)3 |
|
= − |
9 |
. |
|
|
|
|
|
(−3)2 − 3 |
|
||||||||
|
32 − 3 2 |
|
|
|
2 |
|
|||||||
7. Чтобы определить интервалы выпуклости и вогнутости графика функции и точки перегиба, вычислим вторую производную
′′ |
x2 (x2 −9) |
′ |
|
(4x3 −18x)(x2 −3)2 − x2 (x2 −9)2(x2 −3)2x |
|
6x(x2 |
−3)(x2 +9) |
|
|
|
6x(x2 +9) |
||||||||
= |
|
|
= |
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
||
2 |
2 |
|
2 |
4 |
|
|
2 |
4 |
|
2 |
3 . |
||||||||
y |
|
|
|||||||||||||||||
|
|
(x |
−3) |
|
|
(x |
−3) |
|
(x |
−3) |
|
|
|
(x |
−3) |
||||
|
|
|
|
x1 = − |
|
|
x2 = |
|
|
(как и |
|||||||||
|
|
Вторая |
производная не существует в точках |
3, |
3 |
||||||||||||||
сама |
функция) |
и обращается в |
нуль при x = 0. Получившиеся |
|
точки |
||||||||||||||
разбивают числовую ось на четыре интервала. Методом интервалов определяем знак второй производной на каждом из получившихся интервалов:
29
