Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5792

.pdf

Скачиваний:

Добавлен:

21.11.2023

Размер:

667.6 Кб

Скачать

☆

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

ln(х -

π )

(ln(x - π ))'

cos

2 x

(cos

x)'

lim

= lim

tgx

(tgx)'

x→

x -

(x -

x→ 2

= lim - 2 cos x × sin x = 0 .

x→π

Пример 3. Найти предел lim (tgx × ln x) .

x→0

Решение.

Так

как

lim tgx = 0 и

lim ln x = -¥ ,

следовательно, имеем

x→0

неопределенность вида [0 ×¥]. Преобразуем выражение, стоящее под

предела:

lim (tgx × ln x) = lim

ln x

= lim

ln x

= lim

(ln x)'

= lim

- 2 sin 2 x

ctgx

(ctgx)'

x→0

(−2sin 2 x)'

tgx

− 2 sin x cos x

= lim

= 0 .

x→0

Пример 4. Найти предел lim (ctgx)sin x .

x→0

знаком

= 00 =

Решение.

данном

случае

имеем

неопределенность

вида

[∞ 0 ].

Прологарифмируем заданную функцию:

y = (ctgx)sin x

ln y = ln(ctgx)sin x

= sin x × ln ctgx

Далее рассмотрим предел

lim ln y = lim (sin x × ln ctgx) = [0 × ¥] = lim

ln ctgx

= lim

(ln ctgx)'

x→0

x→0 ( 1

sin x

-1

= lim

ctgx

sin 2 x

= lim

sin x

= 0

-1

ctgx × cos x

x→0

× cos x

x→0

x→0 cos 2 x

sin 2 x

Итак, lim ln y = 0 , то есть

= 0

, тогда lim y

= lim (ctgx)sin x = 1 .

ln lim y

x→0

Применение правила Лопиталя при вычислении предела часто приводит к громоздким выражениям. В этом случае целесообразно представить предел в виде произведения нескольких пределов.

	tgx −			x
Пример 5. Найти предел lim	tgx −			cos x		.
Пример 5. Найти предел lim	e x	2	− e− x		2	.
x→0	e x		− e− x
Решение. В данном случае имеем неопределенность вида							0	.

						0

tgx -

sin x

sin x - x

cos x

lim

= lim

cos x

= lim

− x2

2 x2

− x2

2 x2

x→0

e - e

x→0

e × (e

-1)

x→0

cos x × e × (e

-1)

= lim

× lim

sin x - x

= 1

× lim

sin x − x

cos x × e

− x2

2 x2

-1

2 x2

− 1

x→0

= lim

(sin x - x)'

= lim

cos x -1

= lim

× lim

cos x -1

2 x2

- 1)'

2 x2

× 4x

2 x2

x→0

cos x -1

(cos x - 1)'

= 1

- sin x

× lim

= 0 .

x→0

Задание №2

Вычислить предел, используя правило Лопиталя.

Вариант

ln(cos2x )

б) lim

ln(cos5x )

а) lim

arccosx x

x→0

а) lim

(1 - x) × tg

πx

б) lim

ctg(x -1)

ln(1- x)

x→1

× ln(x2 - 5x + 6)

1− x + lnx

а)

lim

x - 3

б) lim

x→3+0

x→1 1- 2x - x2

ex - e− x - 2x

а)

lim

б)

lim

x - sinx

x→1

ln x

x -1

x→0

sinx − xcosx

а)

lim

б) lim

sin3 x

x→0

sin x

x→0

x − arctgx

а)

lim

б) lim

2x3

x→1

x -1

ln x

x→0

а) lim

(1 - x )×ln(1 - x)

б)

lim

etgx -1

x→1-0

x→0 tgx - x

а)

lim

sin 2 x

π − arctgx

б)

lim

x →

x -

x − 1

x→ +∞

2 ln

x + 1

ex − esinx

а)

lim

− ctgx

б) lim

x→0

а) lim (π − 2x)cos x

б)

lim

1 − cos x 2

x→ 2

x → 0

x 2sin x 2

а) lim lnx ×ln(x -1)

−1

б) lim

1+ xsinx

x→1

x→0

а)

lim (tgx )tg 2x

б)

lim

ln(2 - x)

πx

x → π

x→2−0

ctg

а) lim x ×(ln(2+ x)- ln(x +1))

б)

lim

1 - sinx

x→∞

x→π

б)

lim

1 - cos7x

а)

lim

arctgx

xsin7x

x→+∞

x → 0

e x − e − x

а)

lim

sin

+ cos

б)

lim

x→∞

x→0 ln(e − x )+ x − 1

1 - cos2x + tg 2 x

lim x

а)

4 + ln x

б) lim

x × sinx

x → 0

x→0

1 − cosx

а)

lim

(1 − e x )x

б) lim

x →+∞

x→0 x( 1+ x − 1)

1 −

cos x

cosx

б)

lim

а)

lim

x → 0

1 − cos

x→0

cos2x

cosx

а)

lim (π − 2x )

ln tg

+ x

x → 2

б)

lim

sin2x

x → 0

- 1

1+ xsin x

а)

lim

ctgx −

б)

lim

e x 2 - 1

x→0

x→ 0

πx

sin3x − 3xe x + 3x 2

2 −

tg 4

б)

lim

а)

lim

x→ 0

x 3

x→2

arctgx − sin x − 6

а)

lim

xπ− 2arctgx

б)

1+ 5x - e5x

x→+∞

lim

sin 2 4x

x→0

x − sinx

а) lim (cos5x2 )

б) lim

tgx - sinx

x→0

ln(e

+ 3)

+ 2

lnx

б)

lim

а)

lim

x→+∞

1 − 2x 2

x→+∞

а) lim (1+ x )lnx

б) lim

x(ex +1)- 2(ex -1)

x → 0

x→0

tgx

x ×ctgx -1

б)

lim

а)

lim

x→0

а) lim (1+ 3tg2 x)ctg2 x

−1

б)

lim

ех2

x→0

2arctgx2 − π

x→∞

ln(e

)

а) lim (1+ 2x )

б) lim

− e

ln(3 − x)

x →∞

x→3

а)

lim

(ex + x)

б) lim 1 −

cos3x

x→+∞

x→0

ex2 −1

lnsin

πx

x ln(e

−1)

а) lim

б)

lim

sin 2 (x − 1)

x→0

x→1

Применение производной к исследованию функций и

построению их графиков

Производная – мощный инструмент для исследования числовых функций. С помощью производных первого и второго порядка изучаются общие свойства функций. Пользуясь результатами этого изучения, можно составить ясное представление о характере функции и построить ее график.

1) Точки экстремума и участки монотонности функции

Функция y = f (x)	называется возрастающей		(убывающей) на
интервале (a; b), если для любых точек		x1 , x2 (a;b)	таких, что x1 < x2 ,
имеет место неравенство:	f (x1 ) < f (x2 )	( f (x1 ) > f (x2 )).

Теорема.		Если функция y = f (x) дифференцируема				на	интервале
(a; b) и	для	любого x (a;b):	′	( f	′	то	функция
			f (x) > 0		(x) < 0),
y = f (x) возрастает (убывает) на интервале (a; b).
Точка	x0	называется точкой	максимума		(минимума)		функции

y= f (x), если:

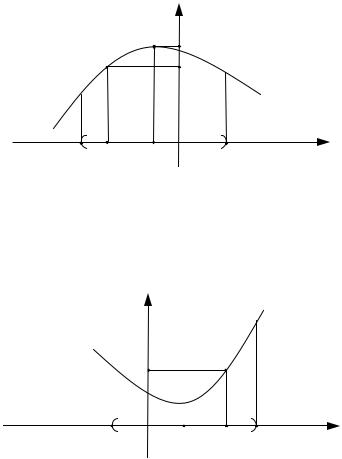
1)функция y = f (x) определена в некоторой ε - окрестности точки x0 ;

2)для любого х ¹ x0 из ε - окрестности точки x0 справедливо

неравенство: f (x) < f (x0 ) ( f (x) > f (x0 )) (см. рис. 1 и 2).

f (x0 )

f (x)

x0 −ε x	x0 0	x0 +ε
	т. max

Рис. 1

f (x)

f (x0 )

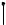
x0 −ε 0	x0	x x0 +ε
	т. min

Рис.2

Точки максимума и минимума функции называются точками

экстремума функции.

Теорема.

(Необходимое условие экстремума). Если

–

точка

экстремума функции

y = f (x),

то в

этой

точке либо

f ′(x0 )= 0 ,

либо

производная не существует.

Точки, в

которых

производная

равна

нулю

либо не

существует,

называются критическими.

Теорема. (Достаточные условия экстремума). Если непрерывная

функция

y = f (x)

дифференцируема слева и справа от критической точки

x0 ,

и при этом ее первая производная меняет знак

с минуса

на плюс

(с плюса на минус) при переходе через точку x0 , то

–

точка минимума

(максимума) функции y = f (x).

Теорема.

(Достаточные условия экстремума).

Если

точке x0

первая производная функции y = f (x) равна нулю ( f '(x0 )= 0 ),

а вторая

производная в точке x0

существует и отлична от нуля (

f ''(x0 )¹ 0 ), то при

f ''(x0 )< 0

в точке

x функция имеет максимум, а при

'(x

)

> 0

функция

имеет минимум.

Пример 1. Найти интервалы монотонности и точки экстремума

функции y =

x -1

Решение.

Областью определения

D данной функции y

является вся

числовая ось R , кроме точки x =1, то есть D = R \ {1}.

Находим первую производную:

′

-1)- x

′

y¢

) ×

× (x -1)

= x -

1 =

(x -1)2

2x × (x -1)- x2 ×1

2x2 - 2x - x2

x2 - 2x

(x -1)2

Используя необходимые условия экстремума, находим критические

точки:

y′ = 0 x2

− 2x = 0

или x(x − 2) = 0 , откуда x1

= 0 или x2 = 2 .

y′ не существует Û (x -1)2

= 0 , откуда x3 = 1.

Используем достаточные условия экстремума. Наносим три

критические

точки

x1 = 0 ;

= 2 ;

x3 = 1 на

область определения D

функции y .

Они разбивают область

D на четыре интервала. Определяем

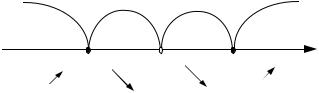
знак функции y′ в каждом интервале.

y′	–	–	+
+

y	0	1	2	x

Так как x1 = 0 D и при переходе через эту точку y′ меняет знак плюс на минус, то x1 = 0 – точка максимума функции y .

Так как x2 = 2 D и при переходе через эту точку y′ меняет знак минус на плюс, то x2 = 2 – точка минимума функции y .

Так как при любом x (− ∞;0) или x (2;+∞) y′ > 0 , то в интервалах

(− ∞;0) и (2;+∞) функция y монотонно возрастает.

Так как при любом x (0;1) или x (1; 2) y′ < 0 , то в интервалах

(0;1) и (1; 2) функция y монотонно убывает.

Пример 2. Найти интервалы монотонности и точки экстремума

функции y = (х -1) × 3 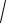х2 .

Решение. Областью определения D данной функции y является вся

числовая ось R .

Находим первую производную

y¢ = ((х -1) × 3

)′ = 1× 3

+ (х -1) ×

3х + 2х

- 2

5х - 2

х2

3 × 3 х

Находим критические точки:

y ′ = 0 5 x − 2 = 0 , откуда x1 = 0,4 .

y′ не существует Û 3

= 0 , откуда x2

= 0 .

Наносим критические точки

x1 = 0,4 ; x2 = 0

на область определения

D функции y . Они разбивают область

D на три интервала. Определяем

знак функции y′ в каждом интервале.

y′

+	–	+
	0	0,4

Так как x1 = 0 D и при переходе через эту точку y′ меняет знак плюс на минус, то x1 = 0 – точка максимума функции y .

Так как x2 = 0,4 Î D и при переходе через эту точку y′ меняет знак

минус на плюс, то x2 = 0,4 – точка минимума функции y .

Так как при любом x (−∞;0) или x Î(0,4;+¥) имеет место y′ > 0 , то в интервалах (− ∞;0) и (0,4;+∞) функция y монотонно возрастает.

Так как при любом x Î (0; 0,4) выполняется y′ < 0 , то в интервале

(0; 0,4) функция y монотонно убывает.

2) Точки перегиба и участки выпуклости графика функции

График дифференцируемой на (a; b) функции y = f (x) называется

выпуклым вверх в интервале (a; b), если он расположен ниже касательной,

проведенной в любой точке x этого интервала (см. рис. 3).

a	x 0	b	x
			Рис. 3
График дифференцируемой на		(a; b)	функции y = f (x) называется

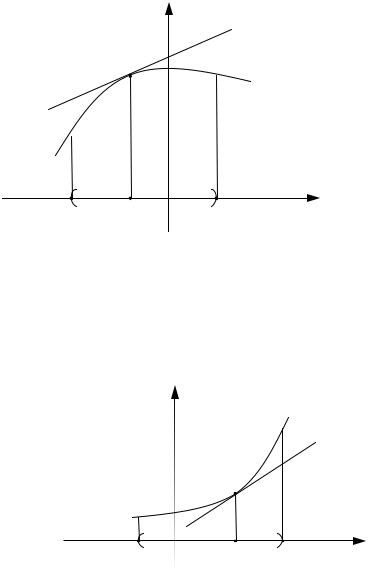
выпуклым вниз в интервале (a; b), если он расположен выше касательной,

проведенной в любой точке x этого интервала (cм. рис. 4).

a 0

Рис. 4

Теорема. (Достаточное условие выпуклости (вогнутости) графика

функции) Если f ′′(x) < 0 в интервале (a; b), то график функции y = f (x)

является выпуклым вверх в этом интервале; если же f ′′(x) > 0 , то в

интервале (a; b) график функции y = f (x) – выпуклый вниз.

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023666.85 Кб05788.pdf
#
21.11.2023666.87 Кб05789.pdf
#
21.11.2023132.72 Кб0579.pdf
#
21.11.2023667.49 Кб05790.pdf
#
21.11.2023667.51 Кб05791.pdf
#
21.11.2023667.6 Кб05792.pdf
#
21.11.2023667.63 Кб05793.pdf
#
21.11.2023667.92 Кб05794.pdf
#
21.11.2023668.05 Кб05795.pdf
#
21.11.2023668.08 Кб05796.pdf
#
21.11.2023668.11 Кб05797.pdf