Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5514

.pdf

Скачиваний:

Добавлен:

21.11.2023

Размер:

623.67 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 88

= -

(x - 7 + x - 3)(x -1)4 - (x - 3)(x - 7)× 4(x -1)3

(x -1)8

= −

(2x −10)(x − 1) − 4(x2 −10x + 21) =

(x −1)5

= −

2x2 − 12x + 10 − 4x2 + 40x − 84

2x2 − 28x + 74

(x − 1)5

Итак,

y′′ =

2(x2 − 14x + 37)

(x − 1)5

y′′ = 0

Используя

необходимое

условие

перегиба,

находим

x1, 2 =

14 ±

x2 −14x + 37 = 0 ,

196 -148

x1, 2 = 7 ± 2

; y′′

или

откуда

не

существует (x −1)5 = 0 , откуда x3

= 1.

Используем достаточные условия перегиба.

y′′

7 − 2

7 + 2

′′

= −1

= −74 < 0 .

y (0)

y′′меняет

= 7 ± 2

Î D и при переходе через эти точки

Так как точки

x1, 2

= 7 ± 2

знак, то x1, 2

–

точки перегиба графика функции y .

′′

Так как при x < 1, 7 − 2 3 < x < 7 + 2

(x) < 0 , то в интервалах (− ∞;1)

, (7 − 2

) функция y выпукла вниз.

3; 7 + 2

1 < x < 7 − 2

x > 7 + 2

′′

Так как при

3 ,

в интервалах

y (x) > 0 , то

(1;7 − 2

), (7 + 2

3;+∞) функция y выпукла вверх.

6. Находим координаты точек пересечения кривой с координатными осями:

Ox : y = 0 (x − 3)2 = 0, откуда x = 3 ;

(0 - 3)2

Oy : x = 0 y = (0 -1)3 =

= -9 .

-1

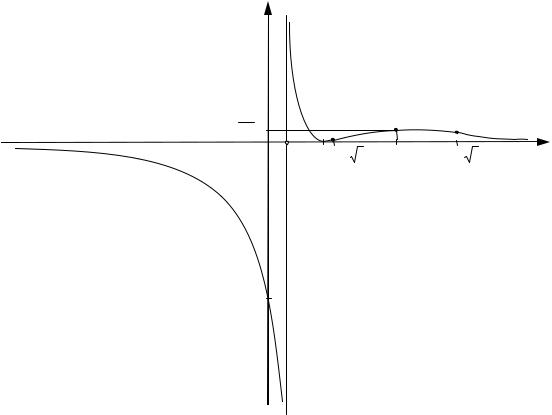
7. Строим эскиз графика данной функции. (См. рис. 65).

y = 0	2
y = 0	27
	0 1 3 7−2 3 7	7+2 3	x

-9

x = 1

Рис. 65

Контрольные задания

Задание 1

Найти матрицу C = AT × B , если:

1.01.		2	3		−1		0
1.01.	A =			, B =					.
		− 4	5				−
		− 4	5		2		−	3
1.02.		0	2			4	−1
1.02.	A =			, B =			.
		− 3
		− 3	1		0		6
1.03.		3	− 2	,		4	3
1.03.	A =			,	B =			.
			4			− 2
	0		4			− 2	1
1.04.	− 3		0	,		2	1
1.04.	A =			,	B =			.
		− 2	1			0
		− 2	1			0	− 3
1.05.		4	−1		0		−1
1.05.	A =		, B =				.
		0
		0	5		1		6
1.06.		2	0	,	− 2		1
1.06.	A =			,	B =			.
						0
	0		− 4			0	5
1.07.		0	− 2	,		1	2
1.07.	A =			,	B =				.
						−1	−
	1		− 3			−1	−	2
1.08.		3	4			0	6
1.08.	A =			, B =					.
		− 5				− 2
		− 5	1			− 2	− 3
1.09.	− 2		0	,	− 4		0
1.09.	A =			,	B =			.
		− 3	1			−1
		− 3	1			−1	6
1.10.	− 4		1			− 2		−1
1.10.	A =				, B =				.
		0
		0	− 5			0			1

Задание 2

Решить систему по правилу Крамера.

3x1 + x2 + 3x3 = 6
	x1 − x2					− x3	= 0 .
2.01.
2x − 3x				2		− 4x = −2
	1					3
4x1 − x2 − x3 = 3
		+ x2 − 5x3					= 2 .
2.02. x1
2x − 3x				2		+ x = −1
	1					3
− x1 + x2 + 5x3 = 5
		− 3x2				− 2x3 = −3.
2.03. 2x1
	x + 2x				2	− 3x	3	= 0
	1
x1 − 3x2 + x3 = 2
		+ x2 − 2x3						= 0 .
2.04. 2x1
3x − x			2	− 5x = −2
	1					3
x1 − x2 + 4x3 = 2
		+ 2x2 − x3						= −3.
2.05. − x1
	x − 3x				2	+ x	= 4
	1					3

3x1 + x2 − x3 = 0
			− 3x3						= −4 .
2.06. x1 − x2
− 2x + x						2	+ 3x = 4
	1								3
x1 − x2 − x3 = −1
							+ 3x3			= 2 .
2.07. − 2x1 + x2
	2x + x			2		− 2x				= 1
	1								3
x − 4x			2			+ x			= 0
	1						3
2.08. 2x1 + x2 + 2x3 = 0 .
2x + 2x					2		− x	3	= 4
	1
4x1 + x2 + x3 = 3
					− x3			= −1.
2.09. x1 + 2x2
x + x		2	+ 3x					= 0
	1						3
− x1 − x2 + x3 = 0
							− x3 = 1 .
2.10. 2x1 + x2
3x − 3x				2		+ 2x = 5
	1								3

Задание 3

Дана пирамида ABCD . Найти:

1)угол ABC грани ABC ;

2)площадь грани BCD ;

3)объем пирамиды ABCD , если

3.01. A( 1; 2;3), B( 0;−1;1), C(−1; 0;−2), D(− 2;3; 0). 3.02. A( 4; 3;1), B( 0;−2;3), C( 3; 0;−3), D(−1;1; 0). 3.03. A( 2;3; 4), B( 0;−1;1), C( 3; 0;−2), D(− 2;3; 0). 3.04. A( 3; 4;1), B( 0;−1;3), C( 2; 0;−1), D(−1; 2; 0). 3.05. A( 4;5; 2), B( 0;−2;1), C(1; 0;−3), D(− 2; 2; 0). 3.06. A( 3; 2;1), B( 0;1; 2), C( 2; 0;−1), D(− 3;3; 0). 3.07. A( 1;3;5), B( 0; 2; −1), C( 2; 0;3), D(− 2;−1; 0). 3.08. A( 1; 4; 6), B( 0;1;−1), C( 2; 0; 2), D(−1;−2; 0).

3.09.A( 2; 4;1), B( 0;−1; − 2), C(1; 0; 2), D(− 2;1; 0).

3.10.A( 3;1; 2), B( 0;−1;−3), C(1; 0;1), D(−1;3; 0).

Задание 4

Дан ABC . Найти:

1)уравнения его сторон;

2)уравнение высоты, опущенной из вершины A на сторону BC ;

3)уравнение медианы AM ;

4)уравнение прямой, проходящей через точку A и параллельной медиане AM , если

4.01. A( 0; 2), B(1; 0), C(− 2;1). 4.02. A( 0;−1), B(− 2; 0), C( 3; 4). 4.03. A( 0;1), B(−1; 0), C( 4;3). 4.04. A( 0;3), B(−1; 0), C(− 2;1). 4.05. A( 0;−2), B(−1; 0), C( 3; 4). 4.06. A( 0; 4), B( 4; 0), C(− 2;−3). 4.07. A( 0;3), B(− 3; 0), C( 2;−3). 4.08. A( 0;1), B(− 3; 0), C( 2;−3).

4.09.A( 0;−1), B(− 3; 0), C( 4; 2).

4.10.A( 0;−2), B( 2; 0), C(−1;1).

Задание 5

Исследовать функцию и построить ее график:

3		3x - x	2
5.1. y = (x −1) .	5.6. y =			.
			2
x2		(x + 2)

5.2. y =

(x2

-1)2

3 .

5.7. y = x ×

x - 3

5.3. y = (x − 2)3 .

5.8. y =

−1

(x -1)3

5.4. y =

2x2 + 3

1 - x4 .

5.9. y =

5.5. y =

2x − 3

5.10. y =

- x2 +1

x2 -1

Литература

1.Важдаев В.П., Коган М.М., Лиогонький М.И., Протасова Л.А. 64 лекции по математике. Книга 1 (лекции 1-39): монография; Нижегор. гос. архитектур.-строит. ун-т – Н.Новгород: ННГАСУ, 2012.– 284 с.

2.Иванова С.В. Построение графиков функций и кривых. – М.:

МФТИ, 2007. – 78 с.

3.Данко П.Е., Попов А.Г., Кожевникова Т.Е. Высшая математика в упражнениях и задачах. Часть 1.– М.: ООО Изд-во «Мир и образование»,

2008 – 368 с.

	Содержание
§1.	Линейная алгебра..............................................................................		3
	Матрицы и действия над ними.....……...……………………...........		3
	Определители......................................................................…… .........		7
	Системы линейных уравнений...………………………………........		8
§2.	Векторная алгебра.............................................................................		10
	Линейные операции над векторами ………………………………	..	11
	Действия над векторами в координатной форме..............................		13
	Скалярное произведение векторов.....................................................		15
	Некоторые приложения скалярного произведения..........................		16
	Векторное произведение векторов.....................................................		17
	Смешанное произведение векторов...................................................		20
§3.	Прямая на плоскости........................................................................		23
	Общее уравнение прямой....................................................................		23
	Взаимное расположение прямых на плоскости................................		32
§4.	Функция одного переменного.........................................................		35
	Основные понятия...............................................................................		35
	Основные элементарные функции.....................................................		38
	Предел числовой последовательности..............................................		43
	Предел функции...................................................................................		47
	Производная.........................................................................................		51
	Производная сложной функции.........................................................		56
	Производные высших порядков.........................................................		57
	Дифференциал функции......................................................................		58
	Правило Лопиталя................................................................................		59
	Исследование функций и построение их графиков..........................		60
	Симметрия функции............................................................................		61
	Асимптоты графика функции.............................................................		62
	Участки возрастания и убывания функции. Точки минимума и
	максимума............................................................................................		63
	Интервалы выпуклости и вогнутости кривой. Точки перегиба.......		65
	Основные требования к результатам исследования и построения
	графика..................................................................................................		67
	Контрольные задания.…………………………………………..........		72
	Литература.……………………………………………………...........		77

Бесклубная Антонина Вячеславовна Павел Валерьевич Столбов

ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. ПРЕДЕЛЫ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.

Учебно-методическое пособие по выполнению контрольной работы по дисциплине «Математика»

для обучающихся по направлению подготовки 38.03.01 Экономика, профиль Бухгалтерский учет, анализ и аудит

Федеральное государственное бюджетное образовательное учреждение высшего образования «Нижегородский государственный архитектурно-строительный университет»

603950, Нижний Новгород, ул. Ильинская, 65. http://www. nngasu.ru, srec@nngasu.ru

<<< < Предыдущая 1 2 3 4 5 6 78 / 88

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023129.94 Кб0551.pdf
#
21.11.2023621.9 Кб05510.pdf
#
21.11.2023622.23 Кб05511.pdf
#
21.11.2023623.02 Кб05512.pdf
#
21.11.2023623.29 Кб15513.pdf
#
21.11.2023623.67 Кб05514.pdf
#
21.11.2023623.76 Кб05515.pdf
#
21.11.2023624.1 Кб05516.pdf
#
21.11.2023624.14 Кб05517.pdf
#
21.11.2023624.26 Кб15518.pdf
#
21.11.2023624.55 Кб05519.pdf