
5133
.pdf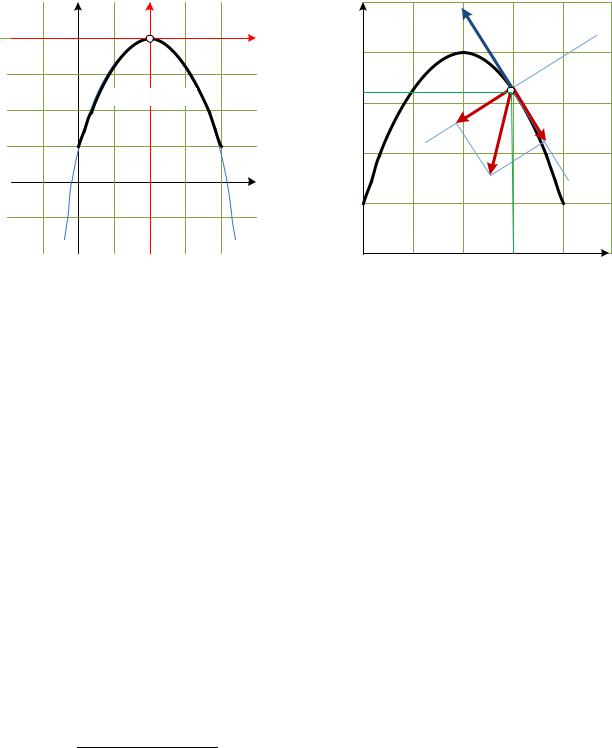
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
при |
|
|
$ 1 %0.75 |
|
|
|
|
, |
|
|
|
|
|
|
|
||||
|
∙ |
при |
$точки |
2 |
, 3.25& и $ 3, 3.25&& |
|
|
|
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
%3.0 |
|
|
|
$точки $0, 1& |
и $ 4, 1&& |
|
|
|||||||
|
|
y |
|
|
y1 |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
4 |
|
|
|
M |
0 |
|
x1 |
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
траектория |
|
|
|
|
|
|
3 |
|
|
R |
|
M1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
|
R |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
aτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
1 |
|
2 |
|
3 |
4 |
x |
|
|
|
|
1 |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
4 |
x |
|
траектория незамкнута. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
определяем |
границы |
траектории, |
|
исходя |
|
из |
неравенства |
|
||||||||||||
|
%1 3 cos 3 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
получим: %1 3 4 3 1, |
|
%2 3 X % 2 3 2, |
|
0 3 X 3 4. |
|
|||||||||||||||
2. |
определяем положение точки М при t=1c. |
1 |
|
|
|
|
|
|
|
||||||||||||
|
6 2 2 !" |
|
|
|
|
|
|
|
|
|
3 м. |
|
|
|
|
|
|||||
|
3 2 2 cos 608 |
2 2 ∙ 2 |
|
|
3 |
|
|
||||||||||||||
|
6 1 3 |
|
1 3 sin |
|
|
8 |
1 3 ∙ |
√3 |
|
|
|
|
|||||||||
|
3 |
60 |
|
= 2 |
? |
1 3 ∙ |
4 |
|
|
||||||||||||
|
|
|
3.25 м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
показываем точку м на рисунке. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3.определяем скорость точки.
для этого определяем проекции вектора скорости на координатные оси:
|
|
|
|
|
2 |
|
|
|
B 2 2 !" 3 |
|
|
|
|||||
@ A |
B |
%2 ∙ = |
3 |
? ∙ 3 |
% 3 |
∙ |
3 |
, |

21
|
B |
1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||
@ A |
B |
2 |
3 ∙ =2 |
3 |
!" |
3 |
? ∙ |
3 |
|||||
|
|
∙ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
3 . |
|
|
|
|
|
|
|
|
|
при t=1c |
608 √ И 1208 |
||||||||||||
sin $1808 % D& 608 √ . |
|
|
|
|
|
|
|||||||
тогда |
@ % |
∙ √ % |
|
%1.81 м⁄с, |
|
|
|
|
|||||
√ |
|
|
|
|
|||||||||
|
|
@ ∙ √ |
2.72 |
м⁄с. |
|
|
|
|
|
||||
изображаем вектор скорости на рисунке. |
|
|
|
|
|
||||||||
вычисляем модуль вектора скорости:
@U@ @ √1.81 2.72 3.27 м⁄с.
4.вычисляем ускорение точки.
для этого определяем проекции вектора ускорения на координатные оси:
|
|
|
|
X YZ[ |
∙\]^Z[_ |
|
|
|
|
|
|
|
|
|
|
|||||||
|
V @A W |
|
|
XYZ_ |
|
|
% ∙ !" |
∙ |
% |
` |
∙ !" |
, |
||||||||||
|
|
|
|
X ∙\]^ [ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
V @A W |
|
X |
|
|
∙ !" ∙ |
|
|
|
∙ !" . |
|
|||||||||||
|
|
!" |
!" 608 |
|
|
!" COS 1208 % . |
||||||||||||||||
при |
T=1c. |
И |
||||||||||||||||||||
тогда |
V % ` ∙ |
|
% `Y %1.10 |
СМY, |
|
|
|
|
|
|
|
|||||||||||
|
V ∙ % |
|
% |
Y |
%3.29 СМY. |
|
|
|
|
|
|
|
|
|||||||||
изображаем вектор ускорения на рисунке. |
|
|
|
|
|
|
|
|||||||||||||||
найдем модуль ускорения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
V UV V √ |
1.10 3.29 |
3.47 СМY. |
|
|
|
|
|
|
|||||||||||||
проектируем вектор ускорения на направление вектора скорости: |
|
|||||||||||||||||||||
|
ghi∙jhi |
|
kgljlmgnjno |
|
$ .p&∙$ .8&m.q ∙$ .`& |
%2.13 |
М |
|
||||||||||||||
|
Vg g |
|
|
g |
|
|
|
|
|
|
. q |
|
СY. |
|
||||||||
проекция отрицательна, то есть движение при Т=1c. является замедленным.
найденная проекция по модулю равна касательному ускорению
|Vs| |Vg|.

22
вычисляем нормальное ускорение:
V^ UV Vs √3.47 2.13 2.74 СМY.
показываем найденные ускорения на рисунке.
5. вычисляем радиус кривизны траектории в данной точке:
t jguY ..q#qY 3.9м.
задача решена 2.2.Преобразование движения
ЗАДАЧА 2
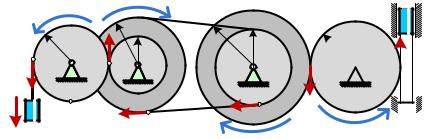
На схеме изображен механизм, передающий движение от тела №1 к телу №6.
Тело №1, которое совершает поступательное движение, имеет скорость равную V1.
Заданы радиусы колес данного механизма – R2, R3, R4, R5, r3=k3·R3, r4=k4·R4. Определить угловые скорости всех колес механизма, линейные скорости точек соприкосновения колес, а также скорость тела №6. Определить скорость и ускорение точки М. Считать, что нити нерастяжимы, а проскальзывание колес и нитей при движении механизма отсутствует.
дано: стержень №1 движется вверх со скоростью @ 120 СМС .
размеры деталей: v w# 20 СМ, v 15 СМ, w wx 30 СМ, w 40 СМ.
M
решение
1.определим направление характер движения тел образующих передачу:
∙тело 1 − движение поступательное вверх;
∙тело 5 − движение вращательное против часовой стрелки;
23
∙ тело 2 − движение вращательное по часовой стрелке;
∙ тело 3 − движение вращательное по часовой стрелке;
∙ тело 4 − движение вращательное против часовой стрелки;
∙тело 6 − движение поступательное вниз.
2.определим скорости точек соприкосновения деталей передачи, используя два положения:
∙две соприкасающиеся точки вращающихся колес имеют равные по величине и направлению скорости;
∙все точки ременной передачи имеют равные по величине скорости.
ω4 |
ω3 |
F |
E |
|
|
|
|
M |
D |
C |
|
|
получим следующие результаты:
 B
B A
A
ω2 ω5 





∙ |
@y @ 120 МС . |
|
88 4 РАДС . |
|||
∙ |
zxwx @y, |
откуда получаем, что zx g|{} |
||||
∙ |
по модулю |
@• 120 МС , |
так как @• @y zxwx. |
|
||
∙ |
z w @•, |
откуда получаем, что z g|‚Y |
#88 3 РАДС . |
|||
∙ |
@ƒ z v , |
откуда получаем, что @ƒ 3 ∙ 20 60 МС . |
|
|||
∙ |
ПО модулю и направлению @† @ƒ, откуда @† |
60 МС . |
||||
∙ |
z w @†, |
откуда получаем, что z g|‡[ |
ˆ88 2 РАДС . |
|||
∙ |
@‰ z v , |
откуда получаем, что @‰ 2 ∙ 15 30 |
М. |
М |
||
∙ |
z#w# @‰, |
|
gŠ |
8 |
С |
|
откуда получаем, что z# |‹ |
8 15 |
С. |
||||
∙ |
по модулю |
М |
ТАК КАК @Œ @‰ z#w#. |
|||
@Œ 30 С , |
||||||
∙@ˆ @Œ 30 МС . движение и скорость тела №6 направлены вниз.

24
R = R
a an
R v
M
3.рассмотрим точку М.
скорость точки м перпендикулярна к радиусу R4 и направлена в
сторону вращения, то есть вправо. по модулю она равна @6 z#w# 15 ∙ 20 30 МС.
вращение тела №4 происходит равномерно. точка М движется по окружности тоже равномерно. по этой причине ускорение точки м направлено по радиусу.
касательное ускорение равно нулю, а нормальное ускорение по
модулю равно
V^ g|•Y 88Y `888 45 СМY.
полное ускорение совпадает с нормальным.
задача решена 2.3. Плоскопараллельное движение твердого тела
ЗАДАЧА 3
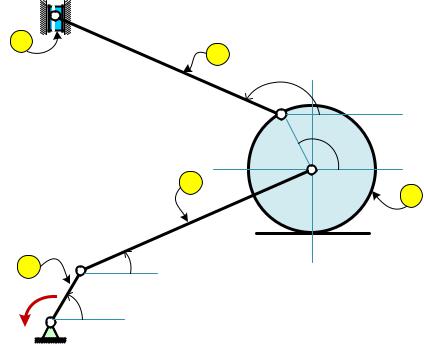
Кривошип ОА вращается вокруг шарнира О с постоянной угловой скоростью ω, приводя в движение последующие звенья кривошипношатунного механизма.
В некоторый момент времени t механизм занимает показанное на схеме положение. Для этого момента времени построить план скоростей. Определить положение МЦС для каждого звена механизма, найти скорости обозначенных буквами точек механизма и угловые скорости всех звеньев и колес механизма. Найти вектор полного ускорения точки В.
Дано: z zŽy 1 РАДС , |
• 608, • 308, • 1208, •# |
1508, |
|
25
OA = 70 СМ, AB = 70 СМ, KL = 70 СМ, R = 20 СМ.
L
ϕ4
K 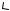 ϕ3
ϕ3
B
ϕ1
|
A |
ϕ2 |
ω |
ϕ1 |
|
|
O |
|
решение
Найдем скорости обозначенных буквами точек механизма и угловые скорости всех звеньев и колес механизма
механизм состоит из пяти тел: звеньев ОА, AB, KL, колеса B и ползуна L. пронумеруем их и рассмотрим их движение.
1.тело 1 (стержень ОА). движение вращательное.
центр скоростей находится в неподвижной точке О, то есть P1=O.
угловая скорость задана, то есть z z 1 РАДС .
определяем модуль скорости точки А.
скорость @iy направлена в сторону вращения перпендикулярно
отрезку ОА.
ее модуль определяется по формуле эйлера: @y z ∙ |•‘| 1 ∙ 15 15 СМС .
2.тело 2 (стержень AB). движение плоскопараллельное.
скорость точки В параллельна опорной плоскости, то есть горизонтальна.
26
восстанавливая перпендикуляры к направлениям скоростей в точках
А и В,
найдем точку Р2 – мгновенный центр скоростей тела 2.
вектор @iy задает направление вращения тела 2 относительно точки
Р2 .
видно, что угловая скорость z направлена по ходу часовой стрелки.
направление вращения z определяет направление скорости точки В (влево).
измеряем отрезки АР2 и ВР2 . |
получаем: АР2 = 119 см и ВР2 = |
69 см. |
|
находим угловую скорость тела 2: |
|
z @А⁄|А’ | 15⁄119 0.13 РАДС .
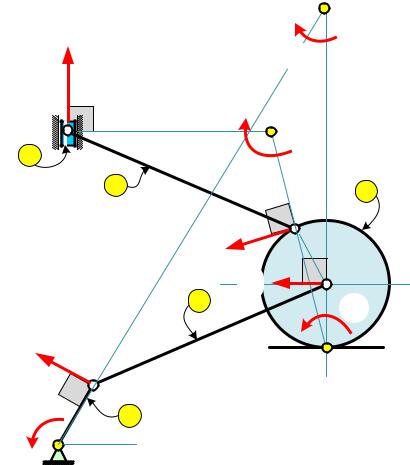
находим модуль скорости точки В:
@• z ∙ |“’ | 0.13 ∙ 69 8.97 СМС .
27 |
|
|
P2 |
R |
ω 2 |
vL |
|
L 90° |
P4 |
|
|
ω 4 |
|
90° |
K |
|
|
R |
|
vK R |
90° |
vB |
B |
R |
ω3 |
vA |
|
A |
P |
90° |
3 |
|
ω1 |
O |
|
|
|
P |
|
1 |
3.тело 3 (колесо B с радиусом ВК).
мгновенный центр скоростей тела 3 расположен в точке
соприкосновения колеса в с опорной плоскостью, то есть в точке Р3 . вектор @iв задает направление вращения тела 3 относительно точки
Р3 .
видно, что угловая скорость z направлена против хода часовой
стрелки.
направление вращения z определяет направление скорости точки
К:
она направлена влево, перпендикулярно к отрезку КР3 .
измеряем отрезок и КР3 . |
получаем: КР3 = 39 см. |
находим угловую скорость тела :
z @•⁄|“’ | 8.97⁄20 0.45 РАДС .
находим модуль скорости точки K:
28
@” z ∙ |•’ | 0.45 ∙ 39 17.55 СМС .
4.тело 4 (стержень kl). движение плоскопараллельное.
скорость точки K направлена перпендикулярно отрезку КР3 . скорость точки L направлена по вертикали (вдоль направляющих ползуна).
восстанавливая перпендикуляры к направлениям скоростей в точках
K и L,
найдем точку р4 – мгновенный центр скоростей тела К
вектор @i” задает направление вращения тела 4 относительно точки
Р4 .
видно, что угловая скорость z# направлена по ходу часовой
стрелки.
направление вращения z# определяет направление скорости точки l
(вверх). |
|
измеряем отрезки KР4 и LР4 . |
получаем: KР4 = 39.5 см и LР4 = |
51 см. |
|
находим угловую скорость тела 4:
z# @”⁄|•’#| 17.55⁄39.5 0.45 РАДС .
находим модуль скорости точки l:
@– z# ∙ |—’#| 0.45 ∙ 51 22.95 СМС .
5. тело 5 (ползун L).
движение тела 5 поступательное.
скорость точки l направлена вверх, а ее модуль равен @– 22.95 СМС .
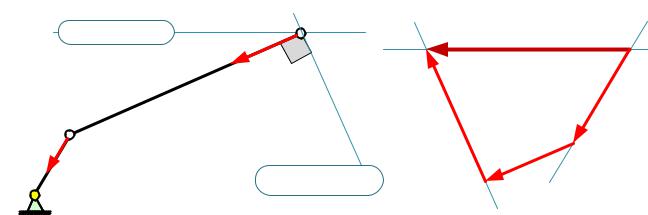
Определим ускорения точек А и В и угловое ускорение звена АВ
29
R
направление aB
|
R |
B |
aB |
|
aBnA |
90° |
Rτ |
|
|
R |
|
aВА |
|
|
A |
|
|
|
|
|
|
R |
|
|
|
|
|
|
R |
R |
|
R |
aA |
aA |
= aAn |
|
an |
|
|
|
|
B A |
|
|
|
R |
τ |
|
O |
направление a |
|
||
|
ВА |
|
||
|
|
|
|
|
кривошип оа вращается равномерно. поэтому касательное (вращательное) ускорение точки а равно нулю, а полное ускорение
точки а равно ее нормальному (центростремительному) ускорению:
Viy Viy^ z ∙ •‘ 1 ∙ 15 15 см⁄с .
чтобы найти ускорение точки в применим теорему о сложении ускорений:
Vi• Viy Vi•y^ Vi•ys . |
|
|
в приведенной формуле направление и величина Viy уже известна. |
||
направление Vi•y^ известно, а его величина находится по формуле: |
||
V•y^ |
z ∙ ‘“ 0.13 ∙ 70 1.18 см⁄с . |
|
известны линии действия ускорений Vi•ys (перпендикулярно отрезку |
||
оа) и Vi• (параллельно опорной плоскости). построим план ускорений |
||
для точки в, начав построение с известных векторов Viy И Vi•y^ (см. |
||
рис.). |
|
|
замерив на чертеже соответствующие отрезки, найдем, что |
||
V•ys |
20.5 см⁄с , |
V• 27.5 см⁄с . |
направление векторов также определяется по чертежу.
угловое ускорение звена ав определим по формуле:
™y• V•ys ⁄‘“ 20.5⁄70 0.3 рад⁄с .
задача решена
