Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5132

.pdf

Скачиваний:

Добавлен:

21.11.2023

Размер:

560.56 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Выполнив под знаком интеграла очевидные тождественные преобразования (возвести разность в квадрат), свели данный интеграл к трем табличным интегралам ∫ xn dx , n = 2;1; 0. постоянная C (которая в данном примере равна сумме трех постоянных C = C1 + C2 + C3 )

появляется тогда, когда исчезают знаки интеграла.

Пример. Найти ∫ x2 + 1 dx . x

Решение.

+ 1

∫

dx =

∫

x +

dx =

∫

xdx +

∫

dx =

=x2 + ln x + C .

Интегрирование заменой переменной.

Во многих случаях ∫ f (x)dx можно упростить, если вместо x

ввести новую переменную t , положив

x = ϕ (t ),

(2)

тогда

dx = ϕ′(t )dt .

Для приведения данного интеграла к новой переменной достаточно привести к новой переменной его подынтегральное выражение

∫ f (x)dx = ∫ f (ϕ ( t ))×ϕ ¢( t ) dt ,

(3)

где

x= ϕ(t ),

всправедливости чего легко убедиться, продифференцировав обе части равенства (3) и воспользовавшись затем формулами (1) и (2).

Метод замены переменной интегрирования, является одним из наиболее эффективных и распространенных методов интегрирования. С другой стороны, не существует общих правил, которые во всех случаях

∫ e2 x+3dx .

позволяли бы найти замену переменной, ведущую к желаемой цели. Поэтому, чем больше примеров самостоятельно решить, тем с большим успехом можно овладеть методом замены переменной.

Пример. Найти

Решение. Данный интеграл не табличный, но есть интеграл ∫ ex dx ,

сходный с данным. Поэтому введем новую переменную t , связанную с x

зависимостью: 2x + 3 = t , x =	1	(t - 3).	Дифференцируя это равенство,

2
получим: (2x + 3)′ dx = (t )′ dt , 2dx = dt ,			откуда dx =	1	dt . Подставив

			2

результат в данный интеграл, имеем:

2 x+3

dx = ∫ e

dt =

+ C.

∫ e

Возвращаясь к переменной x , находим:

∫ e

2 x+3

dx =

2 x+3

+ C .

Для надежности проверяем результат дифференцированием:

2 x+3

′

2 x+3

+ C

(2x + 3)

× 2

= e

–

верно.

Интегрирование по частям.

Пусть u и v –

две любые дифференцируемые функции от x , то есть

u = u(x)

и v = v(x).

Тогда дифференциал произведения u × v вычисляется

по следующей формуле:

d (uv) = udv + vdu .

Отсюда, интегрируя обе части последнего равенства, находим:

∫ d (uv) = ∫ (udv + vdu),

или

u × v = ∫ udv + ∫ vdu ,

откуда
∫ udv = u × v - ∫ vdu .	(4)

Полученная формула называется формулой интегрирования по частям для неопределенного интеграла. Она сводит нахождение интеграла

∫ udv к нахождению интеграла ∫ vdu , и если функции u и v удается подобрать так, чтобы последний интеграл брался проще, чем исходный, то цель будет достигнута.

Пример. Найти ∫ xex dx .

Решение. Пусть u = x , dv = ex dx , тогда du = (x)′ dx = 1× dx = dx ,

v= ∫ ex dx = ex . По формуле (4) находим:

∫xex dx = xex - ∫ ex dx = xex - ex + C ,

∫ xex dx = (x -1)ex + C .

Пример. Найти ∫ x2 ln xdx .

Решение.

Пусть

u = ln x ,

dv = x2 dx , тогда

du = (ln x)′ dx ,

v = ∫ x2 dx =

. По формуле (4) находим:

∫ x2 ln xdx =

ln x - ∫

dx =

ln x -

∫ x2dx =

ln x -

+ C ,

3 3

∫ x

ln xdx = ln x -

+ C .

§ 4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Важным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных понятий математического анализа.

1.Задачи, приводящие к понятию определенного интеграла

Кпонятию определенного интеграла приводят задачи вычисления площадей плоских фигур, длин дуг, объемов тел, вычисление работы, массы неоднородных стержней, центров тяжести плоских фигур и дуг и т.д. Рассмотрим некоторые из них.

2. Площадь криволинейной трапеции

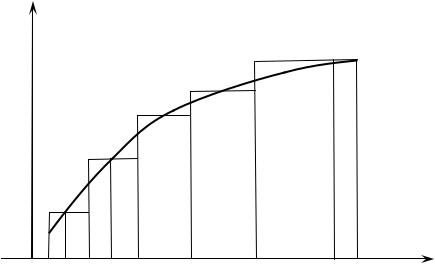
Криволинейной трапецией назовем плоскую геометрическую
фигуру, ограниченную двумя прямыми	x = a и x = b (a < b), отрезком
[a, b] оси OX и графиком некоторой	непрерывной функции y = f (x),

x [a, b] ( f (x) > 0).
y	y = f (x)

x0 = a P1 x1 P2 x2	x n −1	Pn x n = b x
	Рис. 20

Найдем площадь S этой фигуры. Для этого:

1) разобьем отрезок [a, b] произвольно расположенными, но следующими друг за другом точками x0 = a , x1 , x2 ,..., xn = b ;

каждом

из

полученных

отрезков

длины

xi = xi

− xi−1 (i =

= 1, 2,…, n)

1, n

выберем

произвольную

точку

Pi (xi−1 £ Pi £ xi )

и вычислим значение

функции в

этих

точках f (Pi )

(i =

);

1, n

рассмотрим

прямоугольники

основаниями Dxi

высотами

f (Pi )

(i = 1, 2,..., n)

и найдем их площади

f (Pi )× Dxi

(i = 1, 2,..., n).

Сложив эти числа, получим сумму S

= ∑ f (Pi ) xi . Значение полученной

i=1

суммы

приближенно

равно

площади

криволинейной

трапеции

(i = 1, 2,..., n), тем лучше будет

S ≈ ∑ f (Pi ) xi (чем мельче отрезки Dxi

i=1

это приближение);

введем

обозначение: λ = max {Dxi }.

Для

получения

точного

выражения площади S криволинейной трапеции надо перейти к пределу в

λ → 0

и n → ∞

, т.е.

полученной сумме S при

(Pi ) xi .

S = lim ∑ f

λ →0

n→∞ i=1

3. Масса линейного неоднородного стержня

Рассмотрим стержень постоянного

сечения длины b − a

(отрезок

[a, b]). Если стержень однородный, т.е. плотность в каждой

точке

которого постоянна и равна γ , то масса стержня

M вычисляется

по

формуле M = γ ×(b - a).

Пусть

стержень неоднородный

каждой

точке x

известна

плотность f (x).

Найдем массу

этого неоднородного стержня. Для

этого:

разобьем

отрезок

[a, b]

на

отрезков точками

a = x0 < x1 < ... < xn = b ;

xi = xi − xi−1 (i =

) выберем

2) в каждом из полученных отрезков

1, n

Î Dxi ,

i =

вычислим плотность f (Pi )

произвольную точку

1, n

(i =

)

что на каждом отрезке Dxi

1, n

в каждой точке

Pi . Будем считать,

(i = 1, 2,…, n) плотность постоянна и равна

f (Pi ).

Тогда масса участка

Dxi приближенно равна f (Pi )× Dxi ;

) xi . Она приближенно равна массе M

3) составим сумму ∑ f (Pi

i=1

неоднородного стержня;

4) для получения точного выражения массы M стержня перейдем к

пределу при λ → 0, λ = max{ xi } и n → ∞ :

)

M = lim∑ f (Pi

xi .

λ →0

n→∞ i=1

4. Работа переменной силы на прямолинейном участке пути

Допустим, что некоторая сила f = f (x), направленная вдоль оси

OX , на отрезке [a, b] совершает работу (см. рис. 21). Если f = const , то работа A вычисляется по формуле A = f ×(b - a).

Определим работу A переменной силы f (x) на отрезке [a, b]:

f (x)

Рис. 21

Для этого: разобьем отрезок [a, b] с помощью произвольно

расположенных, следующих друг за

другом

точек x0

= a , x1 ,

x2 , ...,

xn = b . Это

разбиение

производим

достаточно мелко, так, чтобы на

xi = xi − xi−1

(i =

)

f (x)

интервалах

1, n

величина

практически не

изменялась.

Пусть

она

равняется

f (Pi ),

Pi Î Dxi , Dxi

= xi - xi−1

i = 1, 2,…, n

( Pi –

произвольно выбранные точки). Величина работы

силы f (Pi

) на участке Dxi

вычисляется по формуле: DAi

= f (Pi

)× Dxi .

Определение. Предел n -ой интегральной суммы для функции

y = f (x)

на

отрезке

[a, b] при

λ → 0

(λ = max{Dxi })

n → ∞

называется определенным интегралом от функции y = f (x) в пределах

от a до b (обозначение ∫b		f (x)dx ), т.е.:
	a
		n	f (P )			=	b	f (x)dx ,
	lim		f (P )	x		=	∫	f (x)dx ,
	λ →0 ∑		i		i		∫
	n→∞ i=1						a
где a –	нижний предел интегрирования,
b –	верхний предел интегрирования,

f (x)dx – подынтегральное выражение,

f (x) – подынтегральная функция.

Одним из геометрических смыслов определенного интеграла

является то, что определенный интеграл равен площади криволинейной трапеции.

Физический смысл определенного интеграла. Здесь его возможности очень широки. В частности, можно определить массу стержня, работу силы на заданном отрезке пути и т.д.

5. Свойства определенного интеграла

Свойства определенного интеграла вытекают из основных свойств сумм и пределов:

1. Постоянный сомножитель можно вынести за знак определенного интеграла:

	b	b	(x)dx , k = const .
	∫ k f (x)dx = k ∫ f		(x)dx , k = const .
	a	a
2.	Определенный	интеграл	от	алгебраической суммы двух
функций	f1 (x) и f2 (x), интегрируемых на [a, b], равен алгебраической
сумме определенных интегралов от этих функций, т.е.
	b		b	b
	∫ [ f1 (x) ± f2 (x)]dx		= ∫ f1	(x)dx ± ∫ f2 (x)dx .
	a		a	a

Данное свойство распространяется и на сумму любого конечного числа интегрируемых функций.

3.Если отрезок интегрирования [a, b] разбит точкой c на два

отрезка [a, c] и [c, b], то интеграл по всему отрезку равен сумме интегралов по его частям:

	∫b	f (x)dx =∫c	f (x)dx +∫b	f (x)dx .
	a	a	c
Точка c может находиться и вне отрезка [a, b].
4.	Интеграл с равными пределами интегрирования (a = b) равен
нулю, т.е.
		∫a	f (x)dx = 0 .
		a

5. Если в определенном интеграле поменять местами пределы интегрирования, то знак интеграла изменится на противоположный:

∫b	f (x)dx = −∫a	f (x)dx .
a	b

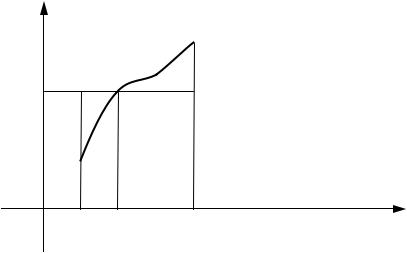
6.Теорема о среднем значении:

Если y = f (x) непрерывна на [a, b], то существует такая точка

c [a, b], что справедливо следующее равенство:

∫b	f (x)dx = f (c)× (b - a).
a

Нетрудно понять геометрический смысл этого равенства: интеграл, стоящий слева есть площадь криволинейной трапеции. Произведение, стоящее в правой части равенства, - площадь равновеликого ей прямоугольника с высотой f (c) и основанием (b − a) (см. рис. 22).

y = f (x)

f (c)

a			c	b	x
				Рис. 22
Число f (c) =		1	∫h	f (x)dx называется	средним значением
Число f (c) =			∫h	f (x)dx называется	средним значением
	b - a a

функции f (x) на отрезке [a, b].

7. Производная от определенного интеграла по переменному верхнему пределу равна значению подынтегральной функции от этого предела:

x		¢	= f (x).
∫	f (t )dt		= f (x).
a	x

6. Вычисление определенного интеграла. Формула Ньютона-Лейбница

Формула Ньютона-Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции.

Теорема. Если F (x) –	одна из первообразных непрерывной на
отрезке [a, b]функции f (x), то			справедлива следующая	формула
Ньютона-Лейбница:
b
∫ f (x)dx =	F (x)	b	= F (b) − F (a).	(4.1)
		b
		a
		a

Доказательство. Доказательство проведем, используя свойство 7. обозначим определенный интеграл с переменным верхним пределом

∫x	f (t )dt через функцию F (x),	т.е.	F (x) = ∫x	f (t )dt . Тогда в силу
a			a
	′	x	′	= f (x). Следовательно,
свойства 7 можно записать (F (x))		= ∫ f (t )dt		= f (x). Следовательно,
		a	x
F (x) является одной из первообразных для интеграла ∫x					f (t )dt . Так как,
				a

все первообразные отличаются на постоянную, то имеет место равенство

∫x	f (t )dt = F (x) + C , a £ x ³ b , где C – некоторое число. Подставляя в
a
это равенство		значение	x = a ,	имеем	∫a	f (t )dt = F (a)+ C
					a
0 = F (a) + C		C = −F (a), т.е.		для	любого x [a, b]		имеем
∫x	f (t )dt = F (x)− F (a).		Полагая	x = b ,	получаем соотношение
a
b	f (x)dx = F (b)− F (a).					F (b)− F (a) = F (x)		b
∫								b
			Обозначим	разность				a .
								a .

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023560.27 Кб05128.pdf
#
21.11.2023560.39 Кб05129.pdf
#
21.11.2023126 Кб1513.pdf
#
21.11.2023560.43 Кб05130.pdf
#
21.11.2023560.48 Кб05131.pdf
#
21.11.2023560.56 Кб15132.pdf
#
21.11.2023560.62 Кб05133.pdf
#
21.11.2023560.68 Кб15134.pdf
#
21.11.2023560.71 Кб15135.pdf
#
21.11.2023560.87 Кб05136.pdf
#
21.11.2023560.92 Кб05137.pdf