
4156
.pdf20
Пример 6.5. |
Разложить |
правильную |
дробь |
|
|
|
|
|
4x + 7 |
|
|
|
на |
||||||||||||||
|
(x2 + 3x + 8)(x2 − 2x + 7) |
|
|
||||||||||||||||||||||||
простейшие дроби. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Согласно формуле (9) разложение запишется в виде: |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
4x + 7 |
|
|
= |
|
M1x + N1 |
+ |
|
M 2 x + N2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||
|
|
|
|
(x2 + 3x + 8)(x2 − 2x + 7) |
x2 + 3x + 8 |
x2 − 2x + 7 |
|
|
|
|
|||||||||||||||||
|
|
d) |
|
В |
случае, |
когда среди |
множителей знаменателя |
имеются |
|||||||||||||||||||
повторяющиеся множители второй степени: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Rα ( x) |
|
|
|
= |
|
|
M1x + N1 |
|
|
|
+ |
|
|
|
|
|
|
|||||
|
(x2 + p1x + q1 )β 1 L(x2 + pr x + qr )β r |
|
x2 + p1x + q1 |
|
|
|
|
|
|||||||||||||||||||
+ |
M 2 x + N2 |
|
+ L + |
|
M β 1 x + Nβ 1 |
+ L + |
, |
|
(10) |
|
|||||||||||||||||
(x2 + p1x + q1 )2 |
(x2 + p1x + q1 )β 1 |
|
|
||||||||||||||||||||||||
|
|
D x + L |
|
D x + L |
|
|
|
|
|
Dβ r x + Lβ r |
|
|
|
|
|||||||||||||
1 |
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+ |
|
+ |
|
+ L + |
|
|
|
|
|
|
|
||||||||||||||||
x2 + pr x + qr |
(x2 + pr x + qr )2 |
(x2 + pr x + qr )β r |
|
|
|
|
|||||||||||||||||||||
|
Пример |
6.6. |
Разложить правильную дробь |
|
|
|
|
7x2 + 3x − 5 |
|
|
|
на |
|||||||||||||||
|
|
|
(x2 − 3x + 8)2 (x2 + x + 4) |
|
|||||||||||||||||||||||
простейшие дроби.
По формуле (10) разложение запишется в виде:
7x2 + 3x − 5 |
= x |
A x + B |
+ |
A x + B |
|
Dx + L |
||||
(x2 − 3x + 8)2 (x2 + x + 4) |
2 − 3x + 8 |
(x2 − 3x + 8)2 |
+ x2 + x + 4 . |
|||||||
|
|
|
1 |
1 |
|
2 |
2 |
|
|
|
Подводя итог вышесказанному, разложение правильной дроби запишется
R (x) |
|
A |
|
|
A |
+ ... + |
|
|
Aγ |
|
+ ... + |
|
|
|
|
|
|
|
||||||
Qm (x) = |
(x − a1 ) + |
(x −1)2 |
|
(x − a )γ1 |
|
|
|
|
|
|
|
|||||||||||||
α |
|
|
|
1 |
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
+ Lβ |
|
|
(11) |
|
|
M |
|
x + N |
|
|
|
|
D x + L |
|
|
|
|
Dβ |
|
|
|
|
|||||||
+ |
1 |
1 |
+ ... + |
+ ... + |
|
r |
|
r |
|
|
|
|||||||||||||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
||||||||||||
x 2 + pr x + qr |
x 2 + pr x + qr |
(x |
2 + p |
r |
x + q |
r |
)βr |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
21
где A1 , A2 ,L, Aγ1 ,L, M1 , N1 ,L, D1 , L1 ,L, Dβr Lβr — неопределённые коэффициенты, которые необходимо вычислить.
Нахождение неизвестных коэффициентов в разложении правильной дроби на простейшие дроби покажем на примерах.
Пример 6.7. Разложить правильную дробь |
|
|
x + 3 |
|
|||||||||||||||||
|
|
|
|
|
на простейшие дроби. |
||||||||||||||||
|
|
x3 − 2x2 + x |
|||||||||||||||||||
Разлагая многочлен x3 - 2x2 + x на множители, |
|
||||||||||||||||||||
x3 - 2x2 + x = x(x2 - 2x +1) = x( x -1)( x -1) = x( x -1)2 |
|||||||||||||||||||||
обнаруживаем, что многочлен имеет три действительных корня |
x1 = 0, x2 = 1 и |
||||||||||||||||||||
x3 = 1, один из которых x1 = 0 — |
|
простой и два x2 = 1 и x3 = 1 — |
кратные. |
||||||||||||||||||
Согласно формуле (11) разложение правильной дроби на простейшие дроби |
|||||||||||||||||||||
запишется в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x + 3 |
= |
|
A |
+ |
B |
+ |
|
C |
(12) |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x( x -1)2 |
x |
x -1 |
( x -1)2 |
|||||||||||||||||
Приведя правую часть равенства к общему знаменателю |
|
||||||||||||||||||||
|
|
x + 3 |
|
|
|
|
|
|
|
( |
) |
|
|
( |
) |
|
|
|
|||
|
|
|
|
= |
|
A |
|
x − 1 2 + B |
|
|
x − 1 x + Cx |
|
|||||||||
|
|
x ( x − 1)2 |
|
|
|
|
|
|
|
x ( x − 1)2 |
|
|
|||||||||
отметим, что дроби с равными знаменателями равны, когда равны их числители. Знаменатели дробей равны, значит должны быть равны и числители, т.е.
x + 3 = A( x -1)2 + B ( x -1) x + Cx .
Приравнивая в тождестве коэффициенты при одинаковых степенях x :
0 × x2 + x + 3 = x2 ( A + B) + x(C - B - 2A) + A,
получим систему 3-х линейных уравнений с тремя неизвестными A, B, C вида:
A + B = 0 при |
x2 |
|
при x . |
-2 A - B + C =1 |
|
|
|
A = 3 при x0 |
|
22
Решая |
|
её, находим |
|
|
A = 3, |
|
B = −3 |
и |
С = 4 . |
Подставляя в (12) |
найденные |
||||||||||||||||||||||||||
значения A, |
|
|
B, |
и С, получим: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 3 |
|
= |
3 |
− |
|
3 |
+ |
|
|
4 |
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x |
− 1)2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 − 2x + x x x − 1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
P |
( x) |
|
|
|
||
Задача |
|
интегрирования |
|
|
выражения |
вида |
n |
dx |
свелась к |
отысканию |
|||||||||||||||||||||||||||
|
Qm ( x) |
||||||||||||||||||||||||||||||||||||
интегралов от простейших дробей. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
I. |
∫ |
|
|
A |
dx = Aln |
|
x + a |
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
x + a |
|
|
|
|
|
|
( |
|
|
|
|
) |
−n+1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x + a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∫ |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
II. |
|
|
|
|
|
dx = A |
|
|
|
|
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
( x + a ) |
n |
|
|
−n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
III. ∫ |
|
|
|
|
Mx + N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
+ px + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
IV. ∫ |
|
|
|
|
Mx + N |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(x2 + px + q)n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Интегралы первых двух дробей найдены. Вычисление интеграла под номером IV выходит за рамки излагаемого материала. Покажем способ вычисления интеграла III.
|
Mx + N |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫ x2 + px + q dx = |
|
обозначая |
t = x |
|
|
+ px + q, |
|
найдём |
dt = (2x + p )dx |
|||||||||||||||||||||||||||
Выполняя тождественные преобразования, получим: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
Mx + N |
|
|
|
|
|
M |
(2x + p) − |
Mp |
+ N |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
∫ |
|
|
|
|
dx = ∫ |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
dx = |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
x |
2 |
|
+ px |
+ q |
|
|||||||||||||||||
|
|
|
|
|
+ px + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
M |
|
(2x + p )dx |
|
|
|
|
|
|
|
Mp |
|
|
dx |
|
|
|
|
|
|||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
+ N − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||
|
2 |
∫ x2 + px + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 ∫ x2 + px + q |
|
|||||||||||||||||||||||
|
|
|
|
|
M |
|
dt |
|
|
Mp |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
||||||||||
= |
|
|
|
|
|
|
+ |
N − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|||||
|
2 |
∫ t |
|
2 |
|
|
∫ |
|
|
|
p 2 |
|
|
|
|
p2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
+ q − |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
23
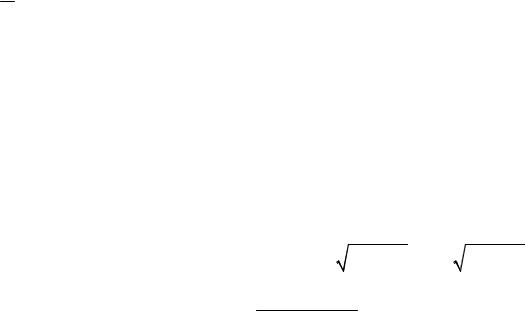
Учитывая, что знаменатель x2 + px + q имеет только комплексные корни,
дискриминант |
p2 |
- q = D < 0 |
тогда -D = q - |
p2 |
> 0 . Обозначая |
q - |
p2 |
= a2 и |
|
|
|
||||||
4 |
|
4 |
|
4 |
|
|||
x + p = u , находим du = dx . 2
Продолжая вычисления, получим:
|
M |
|
|
|
|
|
Mp |
du |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
|
ln |
t |
+ N - |
|
|
|
|
|
|
= |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
2 ∫ u2 |
+ a2 |
|
|
|
|
|
|
||||
|
M |
|
|
|
2 |
|
|
|
|
|
Mp |
|
1 |
|
u |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
ln |
x |
|
+ px + q |
+ N - |
|
|
× |
|
× arctg |
|
+ C |
|||||
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Интеграл равен:
|
Mx + N |
dx = |
M |
ln |
|
x2 + px + q |
|
+ |
2 |
N − Mp |
|
arctg |
2x + p |
|
+ C . |
|
|
|
|
||||||||||||||
∫ x2 + px + q |
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
4q − p2 |
|
4q − p2 |
|
|
|||||
|
|
|
|
|
||||||||||||
3x
Пример 6.8. Найти интеграл ∫ ( x -1)( x + 2) dx .
Подынтегральная функция |
3x |
является правильной рациональной |
( x -1)( x + 2) |
||
дробью (n =1, m = 2, n < m) . Методом |
неопределённых коэффициентов |
|
разложим её на сумму простейших дробей. Согласно формуле (7) разложение запишется в виде:
3x |
|
A1( x+2 |
A2( x−1 |
A1 |
( x + 2) + A2 ( x − 1) |
|
||
|
= |
|
+ |
|
= |
|
|
, |
( x − 1)( x + 2) |
x − 1 |
x + 2 |
|
( x − 1)( x + 2) |
||||
откуда
A1x + 2 A1 + A2 x − A2 = 3x или ( A1 + A2 ) x + 2 A1 - A2 = 3x .
Приравнивая в последнем равенстве коэффициенты при одинаковых степенях x
( A1 + A2 ) × x + (2A1 - A2 ) × x0 = 3x + 0 × x0 ,
получаем систему двух линейных уравнений с двумя неизвестными A1 и A2 :
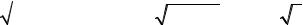
24
|
|
|
|
|
|
|
|
|
x : A + A = 3 |
|
|
Û |
3A = 3 |
|
|
Û |
A =1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x0 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
: 2A1 - A2 = |
|
|
|
|
A2 = 2A1 |
|
|
|
|
A2 = 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
A2 |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
+ |
|
|
|
|
|
= |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
( x -1)( x + 2) |
|
x -1 |
x + 2 |
x -1 |
x + 2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
3x |
|
|
|
dx = |
|
|
|
|
|
|
|
|
1 |
|
|
+ |
|
|
|
2 |
|
|
|
|
= |
|
|
|
dx |
|
|
+ |
|
|
|
2dx |
= |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
∫ ( x -1)( x + 2) |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ x - |
|
|
∫ x |
+ 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
-1 x + |
2 |
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
= ln |
|
x -1 |
|
+ 2ln |
|
x + 2 |
|
|
|
+ C = ln |
|
( x -1) × ( x - 2)2 |
|
+ C. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: |
|
∫ |
|
|
|
|
|
|
|
|
|
|
dx = ln |
|
( x - |
1)( x + 2) |
2 |
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( x -1)( x + 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Пример 6.9. Найти интеграл ∫ |
|
|
|
|
|
|
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
x |
2 |
+ 4x + |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Подынтегральная функция |
|
|
|
|
|
|
|
|
4x |
|
|
|
|
|
|
является правильной рациональной |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x2 + 4x + 3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
дробью (n =1, |
|
m = 2, |
n < m) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Разложим знаменатель этой дроби на линейные множители: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 + 4x + 3 = ( x - x |
)( x - x |
|
|
), где |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
-4 ± 42 - 4 ×1× 3 |
= |
-4 ± |
|
|
|
|
= |
-4 ± |
|
|
= |
-4 ± 2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x = |
16 -12 |
4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1,2 |
|
|
|
|
|
|
|
|
|
|
2 ×1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x = |
-4 + 2 |
= -2 |
= -1, x = |
-4 - 2 |
= -6 = -3. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Тогда x2 + 4x + 3 = ( x + 1)( x + 3) |
и следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
4x |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + 4x + 3 |
( x +1)( x + 3) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Методом неопределённых коэффициентов разложим последнюю дробь на сумму простейших дробей. Согласно формуле (7) имеем:
25
|
|
|
|
|
|
|
|
|
4x |
|
|
|
|
( x+3 |
|
|
|
|
|
|
|
( x+1 |
|
|
|
|
|
A |
( |
x + 3 |
) |
|
+ B |
( |
x + 1 |
|
|
|
|
Ax + 3A + Bx + B |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
+ |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
= |
, |
||||||||||||||||||||||||||||||||||||||
|
|
( x + 1)( x + 3) |
|
|
x + 1 |
|
|
x + 3 |
|
|
|
|
|
( x + 1)( x + 3) |
|
|
|
|
|
|
( x + 1)( x + 3) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( A + B) × x + 3A + B = 4x + 0 × x0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x : A + B = 4 |
|
|
|
|
|
|
-2A = 4 |
|
|
|
A = -2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 : 3A + B = 0 |
Û |
B = -3A |
Û B = 6 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
4x |
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
dx = −2 |
|
|
|
|
|
|
|
|
+ 6 |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|||||||||||||||||||
∫ x2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
+ |
|
|
∫ x + |
|
∫ x + |
|
|
|
|
(13) |
|||||||||||||||||||||||||||||||||||||||||||||||
4x + 3 |
|
|
∫ x + 1 |
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
= −2ln |
|
|
x + 1 |
|
|
+ 6ln |
|
x + 3 |
|
|
+ C |
|
|
|
|
|
|
3x + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Пример 6.10. Найти интеграл ∫ |
|
|
|
|
|
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
x |
2 |
|
+ 2x + |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Выполняя замену |
|
t = x2 + 2x + 5 , найдём dt = (2x + 2)dt . Преобразуем |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
подынтегральную функцию: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
(2x + 2) − |
3 × 2 |
+ 5 |
|
|
|
3 |
(2x + 2) + 2 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + |
2x + 5 |
|
|
|
x2 + 2x + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + 2x + 5 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Интеграл запишется: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
3x + 5 |
|
|
|
|
|
|
|
|
3 |
(2x + 2) + 2 |
|
|
|
|
|
|
|
|
|
|
2x + 2 |
) |
|
dx |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
∫ |
|
|
|
|
dx = ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
∫ |
( |
|
|
|
|
|
|
|
|
|
|
+ 2∫ |
|
|
= |
|
|||||||||||||||||||||||||||||
|
|
x |
2 |
+ 2x + 5 |
|
|
|
|
|
|
2 |
|
|
+ 2x + 5 |
|
|
|
2 |
+ 2x + 5 |
x |
2 |
+ 2x + 5 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
= |
3 |
|
∫ |
dt |
+ 2∫ |
|
|
|
|
|
dx |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
t |
|
+ 2x + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Выделяя полный квадрат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + 2x + 5 = ( x +1)2 -1 + 5 = ( x + 1)2 + 4 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
и обозначая x +1= u, |
|
du = dx , получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
26
|
|
|
|
= |
|
3 |
ln |
|
x2 + 2x + 5 |
|
+ 2∫ |
|
|
|
dx |
|
|
|
|
|
|
= |
|
3 |
|
ln |
|
x2 + 2x + 5 |
|
+ 2∫ |
|
|
|
du |
|
|
|
|
= |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
( x + 1) |
2 |
+ 22 |
|
2 |
|
|
|
u |
2 |
+ |
2 |
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
= |
3 |
ln |
|
x2 + 2x + 5 |
|
+ arctg |
x+1 |
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 6.11. Найти ∫ |
x5 + 4x4 + 18x + 19x2 − 6x + 20 |
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
4 |
+ 2x |
3 |
+ |
10x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Подынтегральная функция является неправильной дробью. Выполняя деление |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 + 4x4 + 18x3 + 19x2 − 6x + 20 |
|
|
x4 + 2x3 + 10x2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 + 2x4 + 10x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
2x4 + 8x3 |
+ 19x2 − 6x + 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x4 + 4x3 + 20x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x3 − x2 |
|
− 6x + 20 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x5 + 4x4 + 18x3 + 19x2 − 6x + 20 |
= x + 2 + |
4x3 − x2 − 6x + 20 |
. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 + 2x3 + 10x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 + 2x3 + 10x2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Разложение на простейшие дроби запишется: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4x3 − x2 − 6x + 20 |
|
|
|
|
4x3 |
− x2 − 6x + 20 A B |
|
|
|
|
|
Mx + N |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
+ |
|
+ |
|
|
|
|
|
|
|
|
(14) |
||||||||||||||||||||||||||||||||||||||
|
|
|
x4 + 2x3 + 10x2 |
|
|
x2 (x2 + 2x + 10) |
|
x |
|
|
|
x2 |
x2 + 2x + 10 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Неопределённые коэффициенты, полученные из решения системы уравнений, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
равны A = −1, B = 2, |
M = 5, |
|
N = −1. Подставим их в выражение (13) и запишем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
интеграл: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫ |
|
x5 + 4x4 + +18x3 + 19x2 − 6x + 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
5x − 1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= |
|
|
x |
+ 2 − |
|
+ |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x4 + 2x3 + 10x2 |
|
|
|
|
|
|
|
|
|
x |
|
x2 |
x2 |
|
+ 2x + |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
(2x + 2) |
− 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
|
|
+ 2x − ln |
|
x |
|
− |
|
+ |
∫ |
2 |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
2 |
+ 2x |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Найдем интеграл
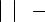
27
|
|
5 |
(2x + 2) − 6 |
|
|
|
|
(2x + 2)dx |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
dx |
||||||||||||||||||||||
∫ |
2 |
|
|
|
|
|
|
|
dx = |
|
∫ |
− 6∫ |
|
|
|
||||||||||||||||||||
2 |
|
|
|
|
|
|
2 |
x |
2 |
+ 2x |
+ 10 |
|
x |
2 |
+ 2x + 10 |
||||||||||||||||||||
|
|
|
x |
+ 2x + 10 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
= |
5 |
ln |
|
x2 + 2x + 10 |
|
− |
6 |
arctg |
|
x + 1 |
+ C |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение запишется в виде: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∫ |
|
x5 + 4x4 |
+ +18x3 + 19x2 − 6x + 20 |
dx = |
x2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 + 2x3 + 10x2 |
|
x + 1 |
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
+ |
5 |
ln |
|
x2 + 2x + 10 |
|
− 2arctg |
+ C. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
5 |
∫ |
dt |
− 6∫ |
dx |
|
= |
|
2 |
t |
( x + 1) |
2 |
+ 32 |
||||
|
|
|
|
|
||||
+ 2x − ln x − 2 + x
§7. ПРИЕМЫ ИНТЕГРИРОВАНИЯ ИНТЕГРАЛОВ, СОДЕРЖАЩИХ КВАДРАТНЫЙ ТРЕХЧЛЕН
Рассмотрим интеграл |
|
|
|
|
I1 = |
|
|
|
|
|
|
dx |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
∫ ax2 |
+ bx + |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Для его вычисления преобразуем квадратный трехчлен ax2 +bx +C к виду: |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
b |
|
|
|
с |
|
|
|
|
|
|
|
|
|
b |
|
|
2 |
|
|
b |
|
с |
|
|
b |
|
2 |
|
||||||||
ax |
|
+ bx |
+ с |
= a × x |
|
+ |
|
|
|
|
x + |
|
|
|
= a x |
+ |
|
|
|
|
|
- |
|
|
+ |
|
|
= a x + |
|
|
± k |
|
|
||||||||||||||||||||
|
|
|
a |
a |
2a |
|
a |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
2a |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Знак «плюс» или «минус», стоящий перед k2 берется в соответствии со знаком |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
c |
|
|
|
|
b 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
выражения |
|
- |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
a |
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Интеграл запишется в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
∫ |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
1 |
∫ |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
ax2 + bx + c |
a |
|
|
|
+ |
b |
2 |
± k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Выполняя замену переменной |
x + |
b |
|
= t , получим dx=dt. Тогда: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
2a |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
∫ |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
1 |
∫ |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
a |
|
b |
2 |
|
|
|
|
2 |
a |
t 2 ± k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
± k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

28
Последний интеграл табличный (см. формулы).
dx
Пример 7.1. Найти интеграл ∫ 2x 2 + 4x − 6 .
Преобразуем знаменатель
2x2 + 4x − 6 = 2(x 2 + 2x − 3) = 2[(x + 1)2 −1 − 3]= 2[(x + 1)2 − 4]= 2[(x + 1)2 − 22 ].
Запишем интеграл в виде:
∫ |
|
|
dx |
= |
1 |
∫ |
dx |
|
|
|
2x |
2 |
+ 4x + 6 |
2 |
(x +1) |
2 |
− 2 |
2 |
|||
|
|
|
|
|
|
|||||
Делаем замену переменной x +1 = t , dx = dt . Подставляя в интеграл, получим:
|
|
|
1 |
∫ |
|
|
dx |
|
= |
|
1 |
∫ |
|
|
|
dt |
|
|
= |
|
1 |
× |
|
|
|
1 |
|
|
|
|
× ln |
|
t - 2 |
|
|
|
+ C . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
(x + 1)2 - 22 |
|
2 |
t 2 - 22 |
|
2 |
2 × 2 |
|
|
|
t + 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
1 |
|
x +1 - 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x -1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
×ln |
|
|
|
|
|
|
|
|
|
|
+ C |
= |
|
|
|
|
ln |
|
|
|
|
|
|
|
+ C . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
2x 2 + 4x + 6 |
8 |
x +1 + 2 |
|
|
8 |
x + 3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 7.2. Найти интеграл |
∫ |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
3x |
2 |
|
+ 9x |
+ |
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Выполним преобразования: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
9 |
|
|
||||||||||
3x |
|
+ 9x + 27 = 3[x |
|
+ 3x + 9]= 3 x |
+ |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
+ 9 = 3 |
x + |
|
|
- |
|
+ 9 |
= |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3 x + 2 |
+ |
|
4 |
= 3 x + |
|
2 + |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Интеграл запишется в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
∫ |
|
|
|
|
dx |
|
|
|
= |
1 |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
+ 9x + 27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
3x |
3 |
|
|
|
|
3 |
2 |
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Заменяя |
x + |
3 |
= t , получим |
dx=dt. Подставляя, интеграл запишется в виде: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

29
|
1 |
∫ |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
|
∫ |
|
|
|
|
dt |
|
|
|
= |
1 |
× |
|
|
2 |
|
|
× arctg |
2t |
|
+ C . |
|||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
3 |
2 |
|
27 |
|
|
|
2 |
|
|
|
27 |
|
27 |
27 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
x + |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
= |
|
|
2 |
|
|
|
arctg |
2x |
+ |
3 |
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3x2 + 9x + 27 3 |
27 |
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Рассмотрим интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
A x + B |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
(2a x + b) + B − |
Ab |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
I2 |
= |
|
|
|
|
|
|
|
dx = |
|
|
|
2a |
|
dx = |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
∫ a x2 |
|
+ b x + |
с |
|
∫ |
|
|
|
a x2 + b x + с |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
A |
∫ |
|
|
2a x + b |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ab |
|
|
2 |
dx |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx + B − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2a a x |
|
|
+ b x + с |
|
|
|
|
|
|
|
|
2 a a x + b x + с |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Последний интеграл есть интеграл I1, вычисленный выше. |
|
|
|
|||||||||||||||||||||||||||||||
Выполняя замену переменной a x2 |
+ b x + с = t , получим (2a x + b) dx = dt . |
|||||||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
A |
|
(2a x + b)dx |
= |
A |
|
dt |
= |
A |
ln |
|
t |
|
+ R = |
A |
ln |
|
a x2 + bx + с |
|
+ R . |
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
2a ∫ a x2 + b x + с 2a ∫ t |
|
|
|
2a |
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Окончательно получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
A x + B |
|
A |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
AB |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
dx = |
|
|
ln |
|
a x |
|
|
+ b x + с |
+ B - |
|
|
|
|
× I1 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
∫ a x2 + b x + с |
2a |
|
|
∫ |
|
|
|
3x + 5 |
|
|
2a |
|
|
|
|||||||||||||||||||
Пример 7.3. Найти интеграл |
|
|
|
|
dx . |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 4x − 6 |
|
|
|
|
|
|
|
||||||||||
Выполняя тождественные преобразования подынтегральной функции, получим:
|
|
3x + 5 |
3 |
(4x + 4) − 3 + 5 |
|
|
|
(4x + 4) dx |
|
|
|
|
|
|
|||||||
∫ |
|
|
dx = ∫ |
4 |
dx = |
3 |
∫ |
+ 2∫ |
|
|
dx |
. |
|||||||||
|
|
|
|
|
|
|
|||||||||||||||
2x |
2 |
+ 4x |
|
|
2x |
2 |
+ 4x − 6 |
4 |
2x |
2 |
+ 4x − 6 |
2x |
2 |
+ 4x − 6 |
|||||||
|
|
− 6 |
|
|
|
|
|
|
|
||||||||||||
Второй интеграл вычислен (см. пример 7.1) |
|
|
|
|
|
|
|
|
|
||||||||||||
В первом интеграле заменяя 2x2 + 4x − 6 = t , получим |
(4x + 4) dx = dt . Интеграл |
||||||||||||||||||||
запишется в виде:
