
4086
.pdf
30
Пример 7.3. Найти интеграл ∫ |
|
3x + 5 |
|
dx . |
|
2x |
2 |
+ 4x |
|
||
|
|
− 6 |
|||
Выполняя тождественные преобразования подынтегральной функции, получим:
|
|
3x + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
(4x + 4) − 3 + 5 |
|
|
|
|
|
|
|
(4x + 4) dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫ |
|
|
|
|
|
|
|
|
dx = |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
∫ |
|
|
+ 2∫ |
|
|
|
|
|
. |
|
|
|||||||||||||||||||||||||||||||||||||||||
2x |
2 |
+ 4x − |
6 |
|
|
|
2x |
2 |
|
|
+ 4x − |
6 |
|
4 |
|
2x |
2 |
+ 4x − 6 |
|
2x |
2 |
+ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x − 6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Второй интеграл вычислен (см. пример 7.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В первом интеграле заменяя |
|
2x2 + 4x − 6 = t , |
получим |
(4x + 4) dx = dt . Интеграл |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
запишется в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
3 |
|
|
∫ |
|
|
(4x + 4) dx |
|
= |
3 |
|
∫ |
|
dt |
= |
|
3 |
ln |
|
2x2 |
+ 4x |
− 6 |
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
2x |
2 |
|
|
+ 4x |
− |
6 |
4 |
|
|
|
|
t |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
3x + 5 |
|
dx = |
3 |
|
|
|
|
|
2x + 4x − 6 |
|
+ |
1 |
|
|
|
x −1 |
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∫ 2x2 + 4x − |
|
|
|
|
x + 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Рассмотрим интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
I3 |
= |
∫ |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при а > 0 и при а < 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a x2 |
+ b x + с |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Если а > 0, то интеграл преобразуется к виду: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
= |
|
|
|
|
1 |
|
|
|
∫ |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
= |
1 |
|
∫ |
|
|
|
|
|
|
|
dx |
|
|
= |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
a x2 + b x + с |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
x2 + px + q |
|
|
|
|
|
a |
|
|
|
p |
2 |
|
p2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
− |
|
+ q |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
= |
|
|
|
1 |
|
|
|
∫ |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
+ |
|
|
p |
|
2 |
|
|
± k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где |
p = |
b |
, |
|
q = |
c |
, а знак перед k2 (см. пример I1). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Выполняя замену x + p = t , интеграл сведется к табличному:
2
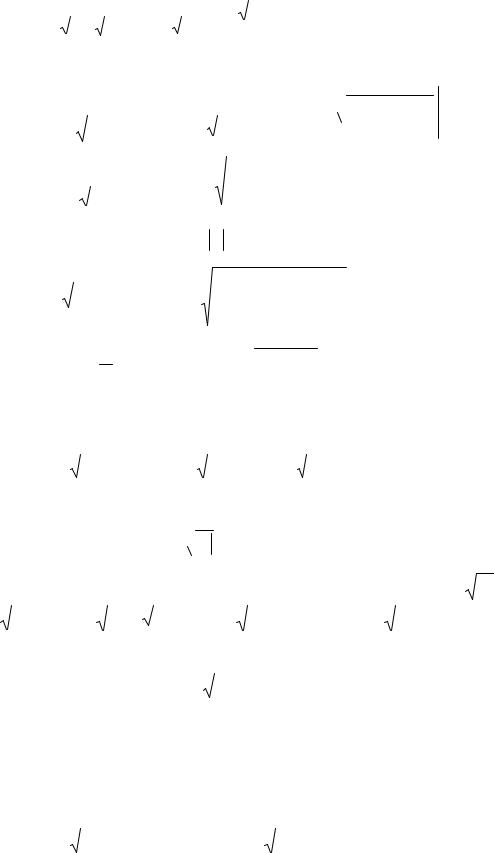
31
1 |
|
|
dt |
|
= |
1 |
ln |
|
t + |
|
|
|
+ C . |
||
|
|
|
|
t 2 ± k 2 |
|
||||||||||
|
|
∫ |
|
|
|
|
|||||||||
|
a |
t 2 ± k 2 |
|
|
|
a |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
Тогда
|
|
|
|
|
|
dx |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
p |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
ln |
x + |
|
|
|
+ |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
∫ a x2 + b x + c |
|
|
|
a |
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||
|
|
1 |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
b |
|
|
c |
|
|
|
|||||||||
= |
|
|
|
|
ln |
x + |
|
|
|
|
+ |
|
|
x |
|
+ |
|
x |
+ |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||||

 x2 + px + q + R =
x2 + px + q + R =
+ R
В случае а < 0, так что а = − а , радикал преобразуется к виду:
|
|
|
|
|
p 2 |
|
|
|
|
|
a (x |
2 |
+ px + q) = |
|
2 |
|
|||||
|
a x + |
|
|
± k |
|
|
= |
|||
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обозначив x + p = t , получим = 
 at 2 ± k 2 .
at 2 ± k 2 .
2
Вычисляемый интеграл преобразуется к табличному
∫ |
|
|
dx |
|
= ∫ |
|
dt |
|
= ∫ |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a x 2 |
+ bx + c |
at 2 |
+ k 2 |
k 2 |
+ at 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
при условии, что знак перед k 2 положительный.
Тогда, выполняя замену 
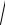
 а t = U , получим:
а t = U , получим:
|
|
dt |
|
= |
1 |
|
|
dU |
|
= |
|
1 |
|
arcsin |
U |
+ C = |
|
1 |
|
arcsin |
|
a |
|
x + C . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
∫ |
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
k 2 + at 2 |
|
|
|
k 2 − U 2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|
k |
|
|
a |
|
|
k |
||||||||||||
Интеграл вида: |
|
|
|
|
|
|
Ax + B |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
∫ |
a x2 |
|
+ bx + с |
|
|
|
|
|
|
|
|
|
|||||||||||
вычисляется с помощью преобразований, аналогичных тем, которые ранее рассмотрены в вычислении интеграла I2:
|
|
|
|
|
|
|
|
A |
|
|
Ab |
|
||
|
|
Ax + B |
|
|
|
|
|
(2ax + b) + B − |
|
|
|
|||
|
|
|
|
|
|
2a |
|
|
||||||
∫ |
|
|
|
dx = ∫ |
|
|
|
2a |
dx = |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
a x2 |
+ bx |
+ с |
|
|
ax2 + bx + с |
|
|
|
||||

32
|
A |
|
(2ax + b)dx |
|
|
Ab |
|
dx |
|
|||
= |
|
∫ |
|
|
|
+ B − |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2a |
|
|
ax2 |
+ bx + с |
|
|||||||
|
|
|
ax2 + bx + с |
2a |
|
|||||||
Выполняя в первом из полученных интегралов подстановку ax2 + bx + C = t ,
получим (2ax + b)dx = dt .
Тогда
A |
|
(2a x + b)dx |
= |
A |
|
dt |
= |
A |
|
|
+ R = |
A |
|
|
+ R . |
||||
|
|
|
|
|
ax2 + bx + с |
||||||||||||||
|
|
|
t |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
2a ∫ ax2 + bx + с 2a ∫ t a |
|
|
a |
||||||||||||||||
|
|
|
|
|
|||||||||||||||
Второй интеграл был рассмотрен (см. I3).
Пример 7.4. Найти интеграл |
∫ |
|
2x − 3 |
||||
|
|
|
|
|
dx |
||
|
|
|
|
|
|||
|
|
|
|||||
|
|
|
2x |
2 |
+ 8x + 1 |
||
Вычисляя производную подкоренного выражения 2a + b = (2x2 + 8x +1)′ , находим,
что 2ax + b = 4x + 8 . Подставляя найденное значение в интеграл, последний запишется в виде:
|
|
2x − 3 |
|
|
|
|
|
|
|
|
2 |
(4x + 8)− 4 − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x + 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
∫ |
|
|
dx = ∫ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
∫ |
|
|
|
|
|
|
|
dx − 7∫ |
|
|
= |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2x2 + 8x + 1 |
2x2 + 8x +1 |
4 |
|
|
2x2 + 8x + 1 |
|
2x2 + 8x + 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
= |
1 |
|
∫ |
dt |
|
− |
7 |
|
∫ |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
= |
|
|
|
|
|
− |
7 |
|
|
∫ |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
t |
2 |
|
|
|
|
|
|
x2 + 4x + |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
(x + 2)2 − 4 + |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
− |
7 |
|
|
|
|
|
|
dV |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
− |
7 |
ln |
V + V 2 − |
7 |
|
|
+ C = |
|||||||||||||||||||||||||||||
|
|
2x2 + 8x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
2x2 + 8x + 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ∫ |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
− |
7 |
|
ln |
x + 2 + x2 + 4x + |
1 |
|
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
2x2 + 8x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 7.5. |
|
Найти интеграл ∫ |
|
|
|
|
|
|
|
|
|
|
2x + 1 |
|
|
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
− 3x |
2 |
|
|
+ 6x |
+ 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
В вычисляемом интеграле а < 0. Выполняя тождественные преобразования подынтегральной функции, получим:

33
|
|
|
|
2x +1 |
|
- |
2 |
(- 6x + 6) + 3 |
|
||||||||
|
|
|
|
|
|
|
|||||||||||
∫ |
|
|
|
∫ |
6 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
dx = |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
- 3x2 |
+ 6x + 9 |
|
|
- 3x2 |
+ 6x + 9 |
|
|||||||||
= - |
2 |
∫ |
|
- 6x + 6 |
dx + 3∫ |
|
dx |
= |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
6 |
|
|
- 3x2 + 6x + 9 |
|
|
|
|
|
- 3(x -1)2 +12 |
|
|||||
Производя замену t = −3x2 + 6x + 9 в первом и втором ( x − 1) = U интеграле,
запишем: |
= − |
1 |
∫ |
dt |
+ 3∫ |
|
|
|
|
|
dU |
|
|
= − |
2 |
|
|
|
|
|
+ |
|
3 |
|
|
3 |
U + C . |
||||||
|
|
|
|
|
|
|
|
− 3x 2 + 6x + 9 |
arcsin |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
3 |
|
|
t |
( |
|
)2 − ( |
|
U )2 |
3 |
|
|
|
|
|
|
|
3 |
|
12 |
|
||||||||||||
|
|
|
12 |
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
2x + 1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
dx = - |
|
|
|
- 3x 2 + 6x + 9 + 3 arcsin |
|
|
(x -1) |
+ C . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|||||||||||||||||||||
|
- 3x 2 + 6x + 9 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
a x + b n |
||||
§ 8. ИНТЕГРИРОВАНИЕ ВЫРАЖЕНИЙ ВИДА R |
|
x, |
|
|
|
|
|||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
c x + d |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим интеграл |
|
|
|
|
|
|
||||||
|
|
|
|
m1 |
|
mα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
n1 |
,..., x |
nα |
|
|
|
|
|
|
|
|
|
∫ R x, x |
|
|
|
dx , где R- рациональная функция своих аргументов, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. |
mi |
– рациональное число. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
ni |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть k – |
наименьшее общее кратное (НОК) чисел {n1 , n2 ,..., nα }. Выполняя |
|||||||||||
подстановку x = t k , получим dx = k t k −1 × dt , что каждая дробная степень х
выразится через целую степень t. Подынтегральная функция преобразуется в рациональную функцию аргумента t.
В интеграле вида:

|
|
|
|
m1 |
|
|
|
n1 |
|||
∫ |
R x, |
a x + b |
|
||
|
|||||
|
|
|
|||
|
|
c x + d |
|
||
|
|
|
|
|
|
выполняя подстановку
a x + b = t k , где c x + d
34
|
|
|
mα |
|
|
|
nα |
||||
|
|||||
,..., |
a x + b |
|
|
dx |
|
|
|
||||
|
|
|
|
||
c x + d |
|
|
|
||
|
|
|
|
|
|
k = НОКi =1−α {ni },
подынтегральная функция преобразуется в рациональную функцию от t. Приемы интегрирования рациональных функций описаны в § 6.
Пример 8.1. |
Найти интеграл |
∫ |
|
|
6 |
x |
|
|
|
dx . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
1 + |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||
В рассматриваемом интеграле n1 = 6, |
|
|
|
|
n2 |
= 3 ; поэтому k = 6. Выполняем |
||||||||||||||||||||||||||||||||||||||||||||||||
подстановку x = t 6 , тогда dx = 6t 5 dt и, следовательно, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x 6 |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
5 |
|
|
|
|
|
|
|
|
t 6 |
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
|
|
1 |
|
|
||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
dx = ∫ |
|
|
|
|
|
|
× 6t |
|
|
dt = 6 |
∫ |
|
|
|
|
|
|
|
|
|
dt = |
6∫ t |
- t |
|
+ 1 - |
|
|
|
dt = |
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
+ t |
2 |
|
|
|
|
|
|
+ t |
2 |
|
|
|
+ t |
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||
1 + x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
t 5 |
|
|
|
|
|
|
|
t 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= 6 |
|
|
|
|
- |
|
|
|
+ t - arctgt |
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
5 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Переходя к «старой» переменной, получим: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
5 |
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
6 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
x 6 |
- 2x |
6 |
|
+ 6x |
6 |
|
- 6arctg x |
6 |
+ C . |
|
|
|
|
|
|
|
|
|||||||||||||||||||
∫1 + 3 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пример 8.2. |
Найти интеграл |
∫ |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
. |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
1 |
- 2x - 3 (1 - |
2x)2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В подынтегральной функции n1 = 2, n2 = 3 , поэтому k = НОК {2,3} т.е. k = 6.
Заменяя 1-2х = t6, получим − 2dx = 6t 5dt . Интеграл запишется в виде:
|
|
|
dx |
|
|
|
- 3t 5 dt |
|
|
t 2 dt |
|
|
t 2 dt |
|
|
|
|
1 |
|||
|
|
|
|
|
|
= |
|
|
= -3 |
|
|
= 3 |
|
|
|
= |
|
t +1 |
+ |
|
dt = |
∫ |
|
|
|
|
∫ |
|
∫ |
|
∫ t -1 |
∫ |
|
||||||||||
|
- 3 (1 - 2x)2 |
|
|
||||||||||||||||||
1 - 2x |
|
|
t 3 - t 4 |
|
1 - t |
|
|
|
|
t -1 |
|||||||||||

35
=3 t 2 + 3t + 3 ln t − 1 + C . 2
Тогда
∫ |
|
|
dx |
= |
3 |
(1 − 2x) |
1 |
+ 3(1 − 2x) |
1 |
+ 3ln |
(1 − 2x) |
1 |
− 1 |
|
+ C = |
||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
3 |
6 |
6 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
− 3 (1 − 2x)2 |
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
1 − 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
=3 3 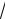 1 − 2x + 36
1 − 2x + 36 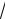 1 − 2x + 3ln 6
1 − 2x + 3ln 6 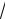 1 − 2x −1 + C . 2
1 − 2x −1 + C . 2
§9. ИНТЕГРИРОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Вэтом параграфе рассматриваются способы интегрирования рациональных функций sin x и cos x, т.е. интегралы виды:
∫R (sin x, cos x)dx
Подстановка tg x = t , которую называют универсальной, рационализирует
2
рассматриваемый интеграл, т.е. сводит его к интегралу от рациональной функции аргумента t.
Из тригонометрии известно, что
|
2 tg |
x |
|
|
|
1 − tg2 |
x |
||
|
|
|
|
|
|
|
|
||
sin x = |
2 |
|
|
|
и cos x = |
|
2 |
. |
|
|
|
|
|
|
|
||||
|
1 + tg2 |
|
x |
1 + tg2 |
x |
||||
|
|
2 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
||
Тогда в соответствии с подстановкой получим:
sin x = |
|
2t |
, cos x = |
1 |
− t |
2 |
. |
|
+ t 2 |
|
+ t |
2 |
|||
1 |
1 |
|
|||||
Выражая из подстановки t = tg x , х как функцию от t, получим: 2
arctgt = arctg tg |
x |
или |
x |
= arctgt , x = 2arctg t |
тогда dx = |
2 dt |
. |
2 |
|
2 |
|
1+ t 2 |
|||

36
Пример 9.1. Найти интеграл ∫ dx . sin x
В соответствии с подстановкой t = tg x интеграл запишется в виде:
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
∫ |
dx |
= ∫ |
1+ t 2 |
× |
|
2 |
dt = ∫ |
dt |
= ln |
|
t |
|
+ C . |
|
|
||||||||||||
sin x |
2t |
1+ t 2 |
t |
|
|
||||||||
|
|
|
|
|
|
||||||||
Тогда
|
dx |
|
x |
|
|
+ C = ln |
|
|
1- cos x |
||||||||
|
= ln |
tg |
|
|
|||||||||||||
∫ sin x |
|
sin x |
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
||||||||
= ln |
|
cosecx - ctg x |
|
+ C |
dx |
|
|||||||||||
|
|
|
|||||||||||||||
Пример 9.2. Найти интеграл ∫ |
. |
||||||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|||||
+ C = ln |
1 |
- ctg x |
+ C = |
|
|||
|
sin x |
|
|
Выполним тождественные преобразования:
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
||
|
|
|
dx |
|
dx |
|
|
d |
+ x |
|
|||||
∫ |
|
= ∫ |
= |
∫ |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
. |
|
||||||
cos x |
π |
|
|
π |
|
|
|
||||||||
|
|
|
|
|
sin |
+ x |
|
|
sin |
+ x |
|
||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
||
|
π |
|
|
|
|
d |
|
+ x |
|
dV |
|
||||
Обозначая V = |
+ x |
, получим |
∫ |
|
2 |
|
|
= ∫ |
. |
||||||
2 |
|
|
π |
|
sinV |
||||||||||
|
|
|
|
|
|
|
sin |
|
+ x |
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
Первообразная последнего интеграла найдена в примере 9.1. Запишем её:
|
|
dV |
= ln |
|
tg |
V |
|
|
+ C . |
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||||
∫ sinV |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
Искомый интеграл равен: |
|
|
|
|
|
|
|
||||||||||
|
|
dx |
= ln |
|
π |
+ |
|
x |
|
|
+ C . |
|
|||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
tg |
|
|
|
|
|
||||||||
∫ cos x |
2 |
|
|||||||||||||||
|
|
|
4 |
|
|
|
|
|
|||||||||
Пример 9.3. Найти интеграл |
∫ |
|
|
|
|
dx |
. |
||||||||||
|
|
|
|
|
|||||||||||||
3sin x − 4cos x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Выполняя универсальную подстановку, получим:

37
∫ |
dx |
= ∫ |
1+ t 2 |
2dt |
= ∫ |
dt |
|
3× 2t - 4(1- t 2 ) × |
|
3t - 2(1- t 2 ) = |
|||
3sin x - 4cos x |
1+ t 2 |
Нахождение последнего интеграла описано в § 7 (см. Интеграл запишем в виде:
1 |
∫ |
|
|
dx |
|
|
|
= |
1 |
∫ |
|
|
dV |
|
|
= |
1 |
× |
4 |
ln |
|
2 |
|
3 |
2 |
9 |
|
2 |
|
2 |
|
5 2 |
2 |
2 × 5 |
|||||||||
|
|
t + |
|
|
- |
|
|
-1 |
|
|
|
V |
|
- |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|||||
dt
∫ 2t 2 + 3t - 2 .
I1).
4V - 5 + C =
4V + 5
|
|
1 |
|
|
16t - 8 |
|
|
|
|
|
1 |
|
|
|
|
|
t - |
1 |
|
|
|
|
|||||||
= |
|
× ln |
|
|
|
+ C = |
|
× ln |
|
|
|
|
|
2 |
|
+ C |
|
|
|||||||||||
|
16t + 32 |
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||||||
|
|
5 |
|
5 |
|
|
|
|
|
t |
+ |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
dx |
1 |
|
|
|
|
tg |
x |
- |
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
∫ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||
|
= |
|
× ln |
|
|
|
|
|
|
|
|
|
|
|
|
+ C . |
|
|
|||||||||||
3sin x - 4cos x |
5 |
tg |
|
x |
|
+ |
1 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Основные случаи применения частных подстановок |
|||||||||||||||||||||||||||
а. В интеграле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∫sinm x ×cosn x dx , где |
m или |
n – |
|
нечетное |
положительное |
целое число. |
|||||||||||||||||||||||
Допустим, что m = 2k + 1, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
∫sin2k +1x ×cosn x dx = ∫cosn x ×sin2k x ×sin x dx = ∫cosn x(1- cos2 x)k sin x dx . |
|||||||||||||||||||||||||||||
Выполняя замену cos x = t , получим - sin x dx = dt , |
sin xdx = −dt. |
|
|||||||||||||||||||||||||||
Интеграл запишется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∫cosn x × (1- cos2 x)k ×sin x dx = -∫t n × (1- t 2 )k × dt , |
а это есть |
интеграл от |
|||||||||||||||||||||||||||
рациональной функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 9.4. Найти интеграл ∫3 sin2 x ×cos3 x dx .
sin2 x ×cos3 x dx .
Показатель степени косинуса нечетное число. Выполняя подстановку sin x = t, cos x dx = dt , получим:

38
∫sin |
23 x ×cos2 x ×cos x dx = ∫sin |
23 x × (1 - sin2 x)×cos x dx = ∫t |
2 |
3 (1 - t 2 )dt = |
|||||||||||
= ∫t 23 dt - ∫t 83 dt = |
3 |
t 53 - |
3 |
t113 + C |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
5 |
11 |
|
|
|
|
|
|
|
|
|||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫3 |
|
× cos3 x dx = |
3 |
(sin x)53 |
- |
3 |
(sin x)113 |
+ C . |
||||||
|
sin 2 x |
||||||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
5 |
|
11 |
|
|
|||
б. В интеграле
∫sinm x ×cosn x dx , где m и n – четные неотрицательные числа.
Применение тригонометрических формул
sin2 ax = |
1 - cos 2ax |
, |
cos2 bx = |
1 + cos 2bx |
|
позволяет понизить степень синуса |
|||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
и косинуса, в конечном счете, свести рассматриваемый интеграл к сумме |
|||||||||||||||
интегралов от констант и нечетных степеней синуса и косинуса. |
|||||||||||||||
Пример 9.5. Найти интеграл |
|
∫sin 4 x ×cos 2 x dx . |
|||||||||||||
Применяя тождественные преобразования, получим: |
|||||||||||||||
|
4 |
|
|
2 |
|
|
|
1 - cos 2x |
|
2 1 + cos 2x |
|||||
∫ sin |
|
x × cos |
|
x dx = ∫ |
|
|
|
× |
|
|
|
× dx = |
|||
|
|
2 |
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
=18 ∫ (1 - 2 cos 2x + cos2 2x)×(1 + cos 2x)dx =
=18 ∫ (1 - cos 2x - cos2 2x + cos3 2x) dx =
=1 ∫ dx - 1 ∫ cos 2x dx - 1 ∫ 1 + cos 4xdx + 1 ∫ cos 2x × (1 - sin2 2x)dx = 8 8 8 2 8
= |
1 |
x - |
1 |
sin 2x - |
1 |
x - |
|
1 |
|
|
|
sin 4x + |
1 |
sin 2x - |
1 |
∫ cos 2x ×sin2 2x dx |
|||||||||||||
|
|
|
16 × 4 |
|
|
|
|
|
|||||||||||||||||||||
8 |
16 |
|
16 |
|
|
|
|
|
16 |
|
|
|
8 |
|
|||||||||||||||
Выполняя замену |
sin 2x = t , |
|
cos 2x × 2dx = dt в последнем интеграле, получим: |
||||||||||||||||||||||||||
|
|
- |
1 |
∫cos 2x ×sin2 2x dx = - |
1 |
|
∫t 2 dt = - |
1 |
× |
t 3 |
+ C . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
16 |
16 |
3 |
|
|
|
|||||||||||||
Тогда |
∫sin4 x ×cos2 x dx = |
1 |
x - |
1 |
sin 4x - |
1 |
sin3 2x + C . |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
8 |
|
64 |
|
|
|
48 |
|
|
|
|
|
|
|
|||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
|
|
Пример 9.6. Найти интеграл |
∫cos 2 x dx . |
|
|||||||||||||
Преобразуем интеграл к виду: |
|
|
|
||||||||||||
∫cos2 x dx = ∫ |
1 + cos 2x |
dx = |
1 |
∫ dx + |
1 |
∫cos 2x dx . |
|
||||||||
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
2 |
2 |
|
|
|
|||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫cos2 x dx = |
1 |
x + |
1 |
sin 2x + C . |
|
|
|
||||||||
|
|
|
|
|
|||||||||||
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
в. В интегралах вида: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫cos m x ×sin n x dx ; |
|
∫cos m x × cos n x dx ; ∫sin m x ×sin n x dx |
|
||||||||||||
применяются следующие формулы (m ≠ n): |
|
||||||||||||||
sin m x × cos n x dx = |
1 |
[sin(m + n)x + sin(m - n)x] , |
|
||||||||||||
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos m x × cos n x dx = |
1 |
[cos(m + n)x + cos(m - n)x], |
(15) |
||||||||||||
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
sin m x ×sin n x dx = 1 [- cos(m + n)x + cos(m - n)x]. 2
Например, подставляя в интеграл и интегрируя, получим:
∫ cos m x ×sin n x dx =
=12 ∫[sin (m + n)x + sin(m - n)x]dx =
=- 1 × cos (m + n)x - 1 × cos (m - n)x + C
2 (m + n) 2 (m - n)
Два других интеграла находятся аналогично.
Пример 9.7. Найти интеграл ∫sin 4x ×sin 6x dx .
Выполняя тождественное преобразование по формуле (15), получим:
∫sin 4x ×sin 6x dx = |
1 |
∫cos 2x dx - |
1 |
∫cos10x dx = |
1 |
sin 2x - |
1 |
sin10x + C . |
|
|
|
|
|||||
2 |
2 |
4 |
20 |
|
||||
