3643

2.1. Предполагая, что наблюдаемая величина Х имеет нормальное распреде-

ление, построим доверительные интервалы для математического ожидания a=М[X]

и среднеквадратического отклонения σ= D( X ) при уровне надежности γ=0,95.

Поскольку известно, что величина t=(Хср-а) 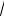n /S имеет распределение Стью-

дента с n-1 степенью свободы, то решая уравнение Р( | t |<tγ )=γ относительно tγ

можно построить симметричный интервал ХВ -εγ <а<ХВ +εγ, в котором с вероятно-

стью γ находится математическое ожидание а. Величина εγ=tγS/ 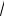n представляет со-

бой точность оценки. Решение tγ=t(γ,n-1) есть обращенное распределение Стьюден-

та, оно протабулировано и может быть найдено и таблиц, например из [1,2 прило-

жение 3]. В рассматриваемом примере tγ =t(0,95;29)=2,045 , εγ = 2,045*2,758/ 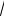30

=1,03 и тогда доверительный интервал для математического ожидания будет

6,367 -1,03< a < 6,367+1,03 или 5,337< a < 7,397.

Для нахождения доверительного интервала оценки среднеквадратического от-

клонения σ воспользуемся тем, что величина

χ2=(n-1)S2/σ2 имеет распределение «Хи-квадрат» с n-1 степенью свободы. Задав-

2.2. Отметим, что построенные доверительные интервалы являются областями принятия гипотез Н0={а=Хср} и Н0={σ=S} при их проверке с уровнем значимости

α=1-γ. Теперь проверим гипотезу о равенстве математического ожидания и диспер-

сии наблюдаемой случайной величины указанным в задании гипотетическим значе-

ниям σ=0,8S, а=1,2Хср.

30

Проверим сначала гипотезу о том, что истинная дисперсия наблюдаемой ве-

личины равна s=0,8S, т.е. Н0={s=0,8*2,785=2,228}. Зададимся уровнем значимости гипотезы a1=0,05 и альтернативными гипотезами Н1 ={s ¹2,228} или Н2

={s>2,228}. Для проверки основной гипотезы воспользуемся критерием «Хи-

квадрат» К=(n-1)(S/s)2.

Наблюдаемое значение критерия kнабл =(30-1) (2,785/2,228)2 =45,313. Крити-

ческая область Ккр при альтернативной гипотезе Н1 двухсторонняя, а критические точки найдем из таблиц kкр.л = c2кр( 1-0.025; 29) = 16,047, kкр.п= c2кр( 0.025; 29) =45,722. Видим, что kнабл не принадлежит критической области и значит, гипотеза принимается, т.е. отличие наблюдаемого значения дисперсии от гипотетического не значительны. Если в качестве альтернативной рассматривать гипотезу Н2, по-

скольку s <S значительно (20%), то при этом критическая область будет правосто-

ронней, а критическую точку kкр= c2кр( 0.05; 29) =42,557 найдем из таблиц. Тогда наблюдаемое значение критерия kнабл =45,313 попадает в критическую область и проверяемая гипотеза отвергается. Результат проверки гипотезы при различных аль-

тернативах оказался разным, в итоге гипотеза отвергается.

Проверим теперь гипотезу о том, что истинное математическое ожидание на-

блюдаемой величины равна а=1,2Хср, т.е. Н0={а=1,2*6,367=7,64}. Зададимся уров-

нем значимости гипотезы a1=0,05 и альтернативными гипотезами Н1 ={а ¹7,64}

или Н2 ={а<7,64}. Для проверки основной гипотезы воспользуемся критерием

Стьюдента К=(Хср-а) 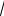n /S.

Наблюдаемое значение критерия kнабл=(6,367-7,64) 30 /2,785=-2,504. Крити-

ческая область Ккр при альтернативной гипотезе Н1 двухсторонняя, а критические точки найдем из таблиц kкр.л= −Ткр(0.025; 29) = -2,045, kкр.п=Ткр(0.025; 29) = 2,045.

Видим, что kнабл принадлежит критической области и значит, гипотеза отвергает-

ся, т.е. отличие наблюдаемого значения дисперсии от гипотетического значительны.

Если в качестве альтернативной рассматривать гипотезу Н2, поскольку а>Хср зна-

чительно (20%), то критическая область левосторонняя, а критическая точка

31

kкр= −Ткр(0.05, 29)=-1,699, тогда наблюдаемое значение критерия kнабл=-2,504 попа-

дает в критическую область и проверяемая гипотеза опять отвергается. Результат проверки гипотезы при различных альтернативах оказался одинаковым, в итоге ги-

потеза отвергается.

2.3. Проверим гипотезу об однородности выборки, т.е. гипотезу о равенстве математического ожидания и дисперсии случайных величин, наблюдаемых в первой и второй половинах имеющейся выборки.

Разобьем выборку на две равные части объемов n1=15, n2=15 и вычислим по ним выборочные средние и выборочные стандарты

Хср1=5,8, Хср2=6,93, S1=2,957, S2=2,576.

Основная проверяемая гипотеза Н0={s1=s2 , а1=а2 }. Зададимся уровнем зна-

чимости гипотезы a2=0,05 и альтернативными гипотезами Н1={s1¹s2} или

Н2={а1¹а2}, поскольку отличия в значениях Хср , S для разных частей выборки не существенны (менее чем 16%).

Для проверки основной гипотезы по отношению к альтернативной гипотезе

Н1 воспользуемся критерием Фишера

Наблюдаемое значение критерия kнабл=1,317. Критическая область Ккр при альтернативной гипотезе Н1 правосторонняя, а критическую точку найдем из таблицkкр = Fкр( 0.05;15;15) =2,403. Видим, что kнабл не принадлежит критической

области и значит, гипотеза принимается. Если в качестве альтернативной рас-

сматривать гипотезу Н2, то для проверки основной гипотезы воспользуемся крите-

рием Стьюдента

Наблюдаемое значение критерия kнабл = -1,119. Критическая область Ккр при этом Н1 двухсторонняя, а критические точки найдем из таблиц

32

kкр.л = −Ткр( 0.05/2; 15+15-2) = -2,048, kкр.п = Ткр( 0.05/2; 15+15-2) = 2,048. Видим, что kнабл не принад-

лежит критической области и значит, гипотеза опять принимается, т.е. отличие на-

блюдаемых значений математического ожидания и дисперсии в первой и второй по-

ловине выборки незначительны. Гипотеза об однородности выборки принимается.

Задание 3

3.1. Построим гистограмму выборки ХВ как удобную форму представления

выборочного распределения. Для этого разобьем наблюдаемый интервал значений в выборке на m равновеликих интервалов

xmin= 1; xmax= 12; m=5; = xmax − xmin =2,2 m

Количество интервалов разбиения m выбирается исходя из свойств выборки, реко-

мендуется использовать формулу m=1+3,2*lg(n), m=5,73 примем m=5. Граничные точки интервалов hj=[xj , xj+1], j=1,.., m и их центры xj+0.5 вычисляем по формулам следующим образом:

Подсчитав для каждого интервала частоты попадания в него элементов выборки nj и

относительные частоты ωj =nj/n , сведем все результаты расчета наблюдаемых час-

тот nj, ωj в следующую таблицу3 и построим гистограмму частот рис. 3.

Таблица 3

33

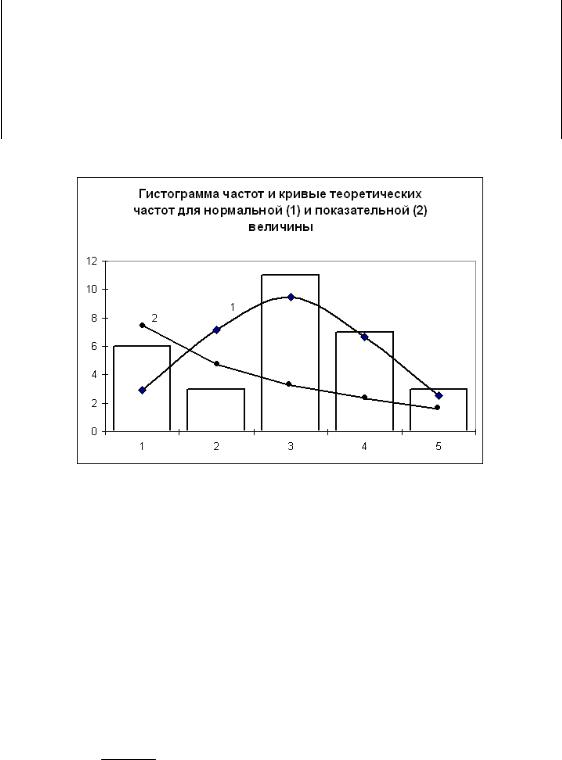
Теоретические частоты показательной случайной величины

Рис.3.

3.2.Используя критерий согласия Пирсона, проверим гипотезу Н0={X~N(a,σ)}

онормальном распределении наблюдаемой случайной величины Х с параметрами

а=Хср, σ=S. Для этого подсчитаем теоретические частоты попадания величины Х в

интервалы hj

njт=nP(xj<Х<xj+1) =n(F (xj+1 )–F(x j)) ≈ n *f(xj+0.5).

Поскольку проверяется гипотеза о нормальном распределении то из таблиц находим

значения F(xj)= Ф( õ j −X ñð ) , где Ф(u)= функция Лапласа, а f(u) - функция Гаусса.

S

Все результаты расчетов теоретических частот njт приведены в таблице 3 и на рис. 3, где приводится так же и кривая теоретических частот.

Согласно критерия Пирсона величина суммарного отклонения наблюдаемых частот от теоретических

34

при условии справедливости основной гипотезы имеет распределение «хи-квадрат» с m-3 степенями свободы и может быть принята за критерий проверки гипотезы Н0.

Задаваясь уровнем значимости ошибки II-рода (отвергнуть верную гипотезу)

α3=0,01 находим критическую точку критерия из решения уравнения

P(χ2 >χ2кр) =α3.

Его решения представляются обратным «хи-квадрат» распределением и находятся из таблиц χ2кр=χ2(α, m-3), например в [1,2 приложение 5]. Тогда критерий проверки основной гипотезы Н0 о нормальном распределении выборочного признака Х

состоит в следующем:

если χ2набл ≤ χ2кр гипотеза принимается (отклонения

теоретических и наблюдаемых частот не значительны),

если χ2набл > χ2кр гипотеза отвергается (отклонения значительны)

В нашем примере величина χ2набл рассчитана в таблице и ее значение

χ2набл=7,407, а χ2кр=χ2(0,01, 2)=9,2 . Тогда согласно критерию Пирсона гипотеза о нормальном распределении случайной величины Х принимается.

3.3. Теперь проверим гипотезу Н0 ={X ~Е( Λ)} о показательном распределе-

нии наблюдаемой случайной величины Х с параметром Λ=1/Хср.

Теоретические частоты подсчитаем исходя из вида функции плотности показатель-

ного распределения

njт ≈ fX(xj+0.5) n ; fX(xj+0.5)= Λ exp( -Λ* xj+0.5 ) .

Рассчитанные теоретические частоты и суммарное относительное отклонение на-

блюдаемых и теоретических частот приводятся так же в таблице 3 и отражены на рис. 3 .

Из таблицы видно, что наблюдаемое значение критерия при проверке гипоте-

зы χ2набл=23,26 принадлежит правосторонней критической области, так как крити-

ческая точка χ2кр=χ2(0,01, 5-2)=11,3. Тогда согласно критерию Пирсона гипотеза о показательном распределении наблюдаемой случайной величи-

ны Х отклоняется.

35

Задание 4

Пусть в опыте наблюдается одновременно значения двух случайных величин

Х, Y (двух признаков). В результате получена двухмерная выборка объема n=30

приведенная в таблице 4.

4.1. Вычислим выборочные средние Хср, Yср выборочные дисперсии Dx, Dy и

среднеквадратические отклонения σxв, σyв по каждому из признаков (признак X

получим выборочное среднее произведение (XY)ср =91,943 и коэффициент корре-

ляции ρВ= 0,538.

Построим прямую линейной среднеквадратической регрессии

Вычислим коэффициенты этой прямой и получим ее уравнение y1 = 0,893x + 7,706 .

Оно представляет собой линейное приближение уравнения регрессии y = M [Y x] и

36

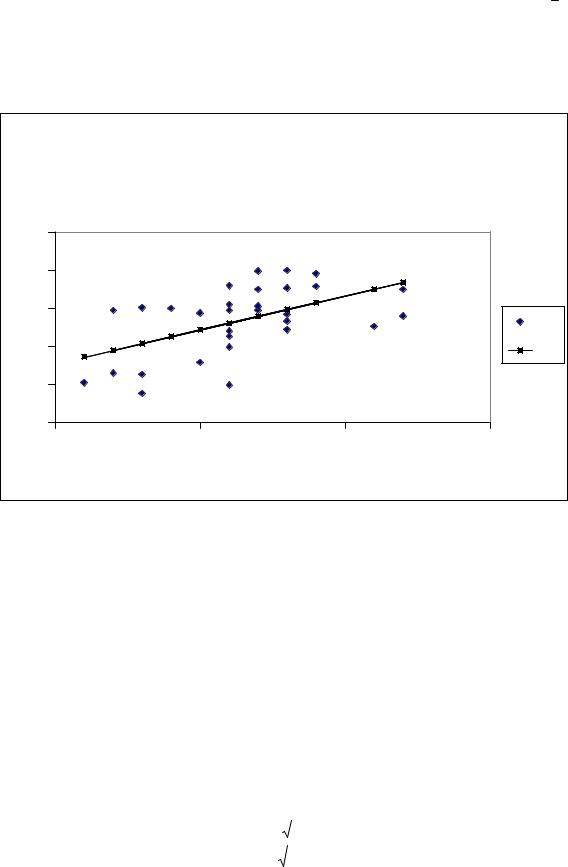
построено методом наименьших квадратов, т.е. сумма квадратов отклонения на-

блюдаемых в выборке точек (xi, yi) от соответствующих точек прямой (xi, y1 (xi)) яв-

ляется минимальной среди всех возможных прямых. Построенная прямая приведена на рис. 4, на нем же приведены и точки выборки.

4.2. Выборочный коэффициент корреляции ρВ является случайной величиной,

поэтому полученное на нашей выборке значение ρВ = 0,538 может не отражать ис-

тинного значения коэффициента корреляции ρ(X,Y).

Проверим гипотезу о значимости выборочного коэффициента корреляции, это позволит судить о наличии корреляционной связи между признаками Х и Y. В каче-

стве основной гипотезы возьмем предположение об отсутствии корреляции

Н0={ρ=0}, допустим так же что двухмерная случайная величина (X,Y) имеет нор-

мальное распределение. Примем за критерий случайную величину

которая, при справедливости основной гипотезы, имеет распределение Стьюдента с n-2 степенями свободы. Тогда, задаваясь уровнем значимости ошибки II-рода

37

(отвергнуть верную гипотезу) a4=0,05 и альтернативной гипотезой Н0={r¹0},

находим критические точки двухсторонней критической области из решения уравнения

P(t >tкр) =a4

Эти решения представляются обратным распределением Стьюдента и находятся из таблиц tкр=Ткр(a/2; n-2), например в [1,2 приложение 6]. Тогда критерий проверки основной гипотезы Н0 об отсутствии корреляции между X и Y состоит в следующем:

В нашем примере tнабл =3,377, а tкр=Ткр(0,025,28)=2,05 и тогда согласно крите-

рию гипотеза об отсутствии корреляции наблюдаемых случайных величин Х и Y

отвергается, т.е. найденный выборочный коэффициент корреляции значим.

38