Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3641

.pdf

Скачиваний:

Добавлен:

21.11.2023

Размер:

378.73 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Ккр={k>kкр}. Задаваясь уровнем значимости ошибки I-рода (отвергнуть верную ги-

потезу) α находим критическую точку kкр однозначно из решения уравнения

∞

P(k>kкр) = ∫ χ 2 (k, m − r − 1)dk = α

kкр

Решение этого уравнения kкр= χ2кр(α, m-r-1) представляет собой обращение функции распределения «хи-квадрат» случайной величины и приводится в много-

численных таблицах, например в [1].

Вычислив по выборке наблюдаемое значение критерия kнабл строим критерий

проверки основной гипотезы Н0 о распределении выборочного признака Х:

если kнабл ≤ kкр гипотеза принимается (отклонения теоретических и наблюдаемых частот не значительны),

если kнабл> kкр гипотеза отвергается (отклонения значительны).

Важным свойством этого критерия является его независимость от предполагаемого вида закона распределения, что позволяет проверить сразу несколько гипотез о виде распределения, а среди допустимых выбрать наиболее правдоподобную, соответствующую min kнабл .

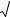
Основная гипотеза	Критерий К и его	Конкурирующая	Критическая	Критические точки
Н0	распределение	гипотеза Н1	область Ккр	kкр
Н0	распределение		область Ккр	kкр

О значении дисперсии	К=(n-1)S2/s02	s2 > s02	k>kкр	kкр = c2кр(a, n-1)
s2 = s02	Критерий “ Хи-квадрат”
по выборке {xj} объема n с	с n-1 степеней свободы.
по выборке {xj} объема n с	с n-1 степеней свободы.	s2 < s02	k<kкр	kкр = c2кр(1-a, n-1)
со средним значением Хср	Закон распределения
	Закон распределения
и выборочным	fК(k)= c2(k , n-1)
и выборочным	fК(k)= c2(k , n-1)	s2 ¹ s02	k>kкр.п ;	kкр = c2кр.п(a/2, n-1);
стандартом S.	М[K] = n-1, D[K]=2(n-1)		k<kкр.л	kкр = c2кр.л(1-a/2, n-1)
	М[K] = n-1, D[K]=2(n-1)		k<kкр.л	kкр = c2кр.л(1-a/2, n-1)

О значении		a ¹ a0	abs (k)>kкр	kкр = Ткр(a/2, n-1)
О значении	К=(Хср – а0) n /S	a ¹ a0	abs (k)>kкр	kкр = Ткр(a/2, n-1)
математического	Критерий Стьюдента
	Критерий Стьюдента

ожидания	с n-1 степеней свободы.	a > a0	k>kкр	kкр = Ткр(a, n-1)
а=а0	Закон распределения
	Закон распределения
по выборке {xj} объема n
по выборке {xj} объема n	fК(k)= T(k , n-1)	a < a0	k<kкр	kкр = -Ткр(a, n-1)
с параметрами Хср , S.	М[K] = 0, D[K]=n-2/n-3
	М[K] = 0, D[K]=n-2/n-3

О сравнении дисперсии	К=(S1/S2)2>1
двух случайных величин	S1=max(Sx,Sy) ~ n1	sx2 > sу2	k>kкр	kкр =Fкр(a, n1, n2)
sx2 = sу2	S2=min(Sx,Sy) ~ n2
по выборкам {xj}, {yj}
по выборкам {xj}, {yj}	Критерий Фишера	sx2 < sу2	k>kкр	kкр =Fкр(a, n1, n2)
объемов nx, ny со средн.	с n1, n2 степен. cвободы.
значениями Хср ,Yср и стан-	Закон распределения
значениями Хср ,Yср и стан-	Закон распределения
дартами Sx, Sy	fК(k)= F(k , n1, n2)	sx2 ¹ sу2	k>kкр	kкр =Fкр(a/2, n1, n2)
	fК(k)= F(k , n1, n2)
	М[K]= n2/( n2-2)>1
	М[K]= n2/( n2-2)>1

Основная гипотеза

Критерий К и его

Конкурирующая

Критическая

Критические точки

Н0

распределение

гипотеза Н1

область Ккр

kкр

О сравнении мат.ожидан. двух

K=( Хср -Yср)*(В1/В2)1/2

аx ¹ ау

abs (k)>kкр

kкр = Ткр(a/2, n)

случайных величин

В1=nx ny(nx+ny -2)/(nx+ny)

аx = ау

В2= ( nx-1 )Sx2 + ( ny-1 )Sy2

по выборкам {xj}, {yj}

Критерий Стьюдента с

аx >ау

k>kкр

kкр = Ткр(a, n)

объемов nx, ny со средн.

n= nх+ny-2 степ. свободы

значениями Хср ,Yср и стандар-

Закон распределения

kкр = -Ткр(a, n)

тами Sx, Sy

fК(k)= T(k , n)

аx<ау

k<kкр

М[K] = 0, D[K]=n-1/n-2

О сравнении дисперсии

неск. случайных величин

К= max(Si2 ) ∑ Si2

i=1

σ12 = σ22= ..= σm2

Критерий Кочрена со

σs2 ¹ σr2

k>kкр

kкр = Gкр(a, n-1,m)

по выборкам объема n с

степен. свободы n-1 и m.

выборочными стандарт.

Закон распределения

S1, S2, … , Sm.

fК(k)= G(k , n-1, m)

О значимости коэффиц.

К= ρв n − 21 − ρ 2

ρ xу ¹ 0

abs (k)>kкр

kкр = Ткр(a/2, n-1)

корреляции двух нормал. слу-

чайных величин X, Y

ρв =

n ( XY )

ср − X срYср

ρ xу = 0

n − 1

S x S y

по выборкам {xj}, {yj}

Критерий Стьюдента

ρ xу > 0

k>kкр

kкр = Ткр(a, n-1)

объемов n со средними

с n-1 степеней свободы,

значениями Хср ,Yср и

стандартами Sx, Sy

fК(k)= T(k , n-1)

М[K] = 0, D[K]=n-2/n-3

ρ xу < 0

k<kкр

kкр = -Ткр(a, n-1)

8. Задания для выполнения расчетно-графической работы.

ЗАДАНИЕ 1

Для заданной выборки Хк={х1, х2, …., хn} из наблюдений за случайной величиной

Хк , где n – объем выборки, к – номер варианта данных в предлагаемой к выполне-

нию РГР, выполнить следующие операции:

1.1. Придумать случайную величину из определенной предметной области, ко-

торая может быть наблюдаема заданной выборкой.

1.2.Построить выборочный ряд и полигон частот ni,

1.3.Вычислить выборочное среднее Хср, выборочную дисперсию DВ, выборочное среднеквадратическое отклонение σВ, выборочную симметрию AВ, выборочный эксцесс EВ. Вычислить исправленную дисперсию DУТ и выборочный стандарт S

ЗАДАНИЕ 2

Полагая, что наблюдаемая случайная величина Хк имеет нормальное распределение выполнить следующее:

2.1. Для заданного уровня надежности γ построить доверительные интервалы для точечных оценок математического ожидания а*=Хср и среднеквадратического от-

клонения σ*=S

2.2. Проверить гипотезы о значении параметров нормального распределения сле-

дующим величинам: а=1,2Хср; σ=0,8S, при уровне значимости α1.

2.3. При уровне значимости гипотезы α2 проверить гипотезу об однородности выборки т.е. гипотезу о равенстве параметров случайных величин, наблюдаемых в первой и второй половине заданной в варианте выборки.

ЗАДАНИЕ 3

Используя критерий Пирсона проверить гипотезы о виде распределения наблюдае-

мой случайной величины Хк при заданном уровне значимости ошибки α3. 3.1.Построить гистограмму частот nj, j=1,….m , где m – число групп наблюдае-

мых значений

3.2. Проверить гипотезу о нормальном распределении наблюдаемой случайной величины Хк с параметрами а=Хср ; σ=S, построить графики теоретических частот nтj на плоскости гистограммы

3.3. Проверить гипотезу о показательном (экспоненциальном) распределении на-

блюдаемой случайной величины Хк с параметром Λ=1/Хср, построить графики тео-

ретических частот nтj на плоскости гистограммы

ЗАДАНИЕ 4

Для заданных выборок Хк={х1, х2, …., хn} и Хр={х1, х2, …., хn} из наблюдений одно-

временно за двумя случайными величинами ХК и ХР , где к, р – номера сопряжен-

ных вариантов данных в предлагаемой РГР, выполнить следующие операции:

4.1. Вычислить выборочный коэффициент корреляции ρВ(ХК,ХР) для наблюдае-

мых величин ХК, ХР. Построить прямую линейной среднеквадратической регрес-

сии хК” =АхР+В, изобразить ее вместе с наблюдаемыми точками на плоскости хК, хР . 4.2. Проверить гипотезу о значимости выборочного коэффициента корреляции

ρВ(ХК, ХР) при заданном уровне значимости α4.

Данные выборки для величин ХК, где к номер варианта РГР

к=	1	2	3	4	5	6	7	8	9
x1	308	0,6	2,9	512	21,2	449	10	23	12
x2	424	4,5	3,1	659	32,6	1062	11,6	17	18
x3	359	0	2,95	815	44,4	1971	10,7	36	22
x4	438	-5,6	3,1	594	64,4	4147	11,6	10	-2
x5	468	6	3,9	678	39,5	1560	17,2	19	8,4
x6	149	-3,5	3,1	714	32,1	1030	11,6	22	14
x7	534	8	3,35	426	31,7	1004	13,22	6	11
x8	151	3,3	3,3	503	30,2	912	12,9	14	20
x9	803	11,3	3,27	487	33,5	1122	10,7	2	15,4
x10	723	12,2	3,8	543	22,7	515	16,4	34	-3
x11	1000	22,3	3,7	746	21,2	449	15,7	25	12,3
x12	957	20,7	3,9	673	20,4	416	17,2	18	20,1
x13	1086	12,3	2,6	678	15,7	247	8,7	20	11
x14	44	-6,7	4,1	874	36,6	1339	9,3	38	13,6
x15	182	0	2,85	713	48,7	2371	10,12	22	-1,4
x16	550	8,5	2,78	743	36,5	1332	9,7	25	14,1
x17	239	-0,8	4,1	700	42,8	1831	18,8	21	4
x18	741	24,5	2,67	763	38,1	1451	9,3	14	-20
x19	856	11,5	4,4	743	35,4	1253	21,4	5	-11
x20	401	-4,6	2,8	1012	40	1400	9,8	35	-5,6
x21	442	5,3	4,35	699	34,2	1169	21	12	2,2
x22	743	14,3	3,7	972	33,8	1142	15,7	34	2
x23	810	15,4	2,54	820	64,5	4160	8,5	31	11
x24	446	9,7	3,7	630	40,5	1640	15,7	14	7
x25	144	-3,7	2,95	590	40	1600	10,6	10	5
x26	876	-0,5	2,9	610	22	484	10,4	12	0,3
x27	598	9,9	3,2	450	31	961	12,2	9	13
x28	977	21,3	3,5	720	45	2025	14,3	23	14,8
x29	690	3,7	2,7	512	36	1296	9,2	12	8,6
x30	624	10,7	2,65	431	28	784	9	7	3,4
γ	0,95	0,99	0,999	0,95	0,99	0,999	0,95	0,99	0,999
α1	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05
α2	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05
α3	0,01	0,025	0,05	0,025	0,01	0,05	0,025	0,05	0,01
α4	0,1	0,05	0,02	0,01	0,1	0,05	0,02	0,01	0,1
р= 2		3	17	5	6	7	8	4	25

Данные выборки для величин ХК, где к номер варианта РГР

к=	10	11	12	13	14	15	16	17	18	19
x1	16,4	92	25	10	444	2,63	10	8,1	140	930
x2	20,5	215	36	9	370	2,81	9	7,6	260	900
x3	6	397	48	15	292	0,06	73	8,2	140	860
x4	17,6	832	68	12	403	1,51	25	7,6	70	790
x5	18,7	315	43	2	361	7,99	33	8	90	750
x6	12,1	209	36	5	343	6,04	37	7,8	210	710
x7	14,4	203	35	5	487	0,2	54	8,3	100	560
x8	16,2	185	34	10	448	2,77	20	8,1	110	320
x9	12,4	227	37	9	456	2,94	48	7,3	50	270
x10	15	106	26	8	428	1,23	5	7,5	470	2830
x11	17,5	92	25	9	327	3,37	63	7,9	380	2440
x12	20,2	86	24	8	363	7,55	42	7,6	340	2270
x13	19,6	52	19	12	361	1,75	26	8	360	1760
x14	20	270	40	10	263	2,46	89	7,9	330	1720
x15	17,7	477	52	11	343	2,59	53	8,3	260	1580
x16	7,2	469	40	13	328	0,99	99	8,2	270	1530
x17	19,3	369	46	16	350	0	1	7,6	260	1460
x18	7	293	42	13	318	0,95	90	7,7	190	1070
x19	6,4	253	39	3	328	1,14	25	8	160	1050
x20	10	289	44	11	194	1,25	29	8	200	930
x21	12,3	236	38	9	350	2,41	12	7,9	230	2560
x22	13,7	231	37	13	214	1,27	80	8,3	140	910
x23	18,3	835	68	14	290	0,54	79	7,7	170	860
x24	13,5	331	44	13	385	1,06	99	7,8	100	550
x25	13,7	323	43	10	405	2,51	70	7,9	90	790
x26	11	99	26	10	395	2,37	66	8,05	110	330
x27	16,8	195	35	11	475	2,24	6	8	480	2450
x28	11,9	405	49	8	340	3,9	57	7,9	310	1780
x29	13,8	262	40	7	444	3,7	47	8,3	260	1100
x30	16,1	159	32	2	484	8,18	17	7,55	210	840
γ	0,95	0,99	0,999	0,95	0,99	0,999	0,95	0,99	0,999	0,95
α1	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05
α2	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05
α3	0,025	0,05	0,05	0,025	0,01	0,05	0,025	0,05	0,01	0,05
α4	0,05	0,02	0,01	0,1	0,05	0,02	0,01	0,1	0,05	0,02
р=	30	8	5	26	4	11	12	13	19	15

Данные выборки для величин ХК, где к номер варианта РГР

к=	20	21	22	23	24	25	26	27	28	29	30
x1	14,7	3	12,4	341	140	97,5	3,42	2120	340	0,71	51,3
x2	14,4	2	11,2	405	260	90	3,51	1820	260	0,75	65
x3	19,9	2	10,9	344	140	85	2,03	1750	240	0,02	16,5
x4	16,9	1	13	830	70	115	2,87	1560	320	0,44	55,4
x5	4	2	12,9	244	90	102	5,41	1540	345	1,7	59,1
x6	7,9	3	11	237	210	95,1	4,76	1490	280	1,38	37,1
x7	19,6	4	12	178	100	98,2	4,73	1370	170	1,36	44,6
x8	14,5	1	10	161	110	87	3,47	1340	290	0,74	50,7
x9	14,2	1	10,5	31	50	93,3	3,56	1270	210	0,78	38
x10	17,4	5	13,1	917	470	116,1	3,97	1245	150	0,98	46,6
x11	13,3	2	10,7	752	380	91,5	3,76	540	220	0,87	55
x12	4,9	3	10,2	704	340	87,3	3,85	1040	280	0,93	64
x13	16,5	1	9,2	515	360	98,7	3	2260	320	0,5	62
x14	15,1	2	9,3	445	330	95,5	3,34	2460	390	0,67	63
x15	14,8	3	11	494	260	94	3,2	1270	100	0,7	55,5
x16	18	2	10,7	476	270	94,8	2,61	580	140	0,3	22,4
x17	20	5	13	504	260	107,5 1,98		920	135	-0,01	61
x18	18	3	13	720	190	137,5	2,57	1160	200	0,29	20
x19	17,7	1	12,5	399	160	127	2,68	1300	240	0,34	18,1
x20	17,5	3	11,9	473	200	119,5	2,7	1350	250	1,23	30,3
x21	15,2	2	12,8	369	230	109,7	3,31	1440	200	0,66	37,1
x22	17,5	1	11,6	230	140	110	2,75	1650	350	0,376	42,3
x23	18,9	3	12,4	231	170	98,1	2,34	2310	270	0,17	57,7
x24	17,9	4	12,5	265	100	103	2,63	1720	260	0,32	41,8
x25	15	2	11	158	80	105,5	3,36	1040	280	0,68	42,5
x26	15,3	3	13,3	871	350	92,7	3,31	1380	150	0,65	63,1
x27	15,5	5	10,2	478	290	93,1	3,24	1920	290	0,62	52,7
x28	12,2	3	9,6	265	170	94	3,95	1490	280	0,98	36,3
x29	12,6	2	13,7	190	120	101,7	3,89	1560	320	0,94	43,1
x30	3,7	3	12,6	457	410	108,3	5,46	2110	110	1,73	50,4
γ	0,99	0,999	0,95	0,99	0,999	0,95	0,99	0,999	0,95	0,99	0,999
α1	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05
α2	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05
α3	0,05	0,025	0,05	0,05	0,01	0,025	0,05	0,05	0,025	0,05	0,01
α4	0,01	0,1	0,05	0,02	0,01	0,1	0,05	0,02	0,01	0,1	0,05
р=	16	22	18	19	23	14	27	28	29	26	9

9. Пример выполнения расчетно-графической работы

Пусть задана выборка

XB ={2;5;7;1;12; 5;9;6;8;6; 8;6;2;3;7; 6;8;3;8; 12; 6;7;3;9;4; 7;6;8;11;6}

объема n=30, полученная при наблюдении за случайной величиной Х (признак вы-

борки). Заданы так же надежность γ=0,95 для построения доверительных интерва-

лов оценок параметров распределения случайной величиной Х, уровни значимости

α1=0,05; α2=0,05; α3=0,014 α4=0,05 для проверки статистических гипотез.

Задание 1

1.1. Наблюдаемая выборка может представлять собой стаж работы по специ-

альности сотрудников строительного предприятия.

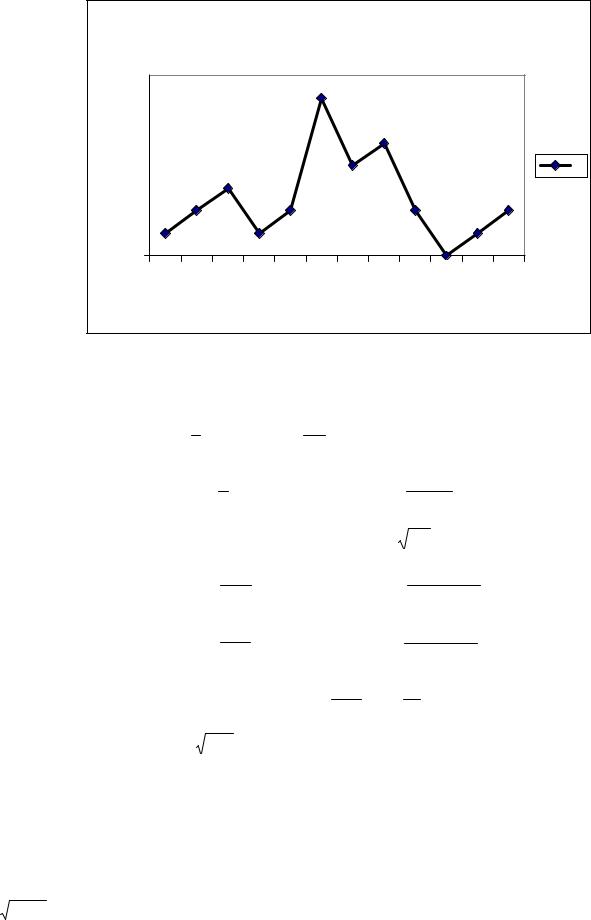
1.2. Построим вариационный ряд выборки, исключив из нее повторяющиеся варианты xj и подсчитав их частоты nj. Получим так же и относительные частоты ωj

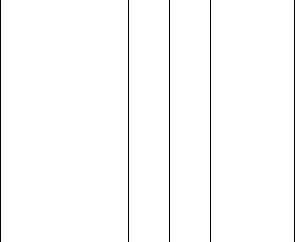
=nj/n. Результат приведен в таблице 2, а на рис. 2 построен полигон частот для за-

данной выборки

Таблица 2

xj	1	2	3	4	5	6	7	8	9	10	11	12	∑

nj	1	2	3	1	2	7	4	5	2	0	1	2	30

ωj	0,0330,067		0,1		0,0330,0670,2330,133			0,1670,067		0	0,03	0,067	1

nj*xj	1	4	9	4	10	42	28	40	18	0	11	24	191

xj-Xср	-5,37 -4,37		-3,367	-2,37	-1,37 -0,37		0,633	1,6332,633		3,63	4,63	5,633

nj*(xj-Xср)2	28,8 38,14		34		5,6013,7360,9411,604			13,3413,87		0	21,5	63,47	224,97

nj*(xj-Xср)3	-155	-167	-114,5	-13,3	-5,11 -0,35		1,016	21,7936,52		0	99,5	357,5	62,058

nj*(xj-Xср)4	829,5727,2		385,4		31,376,9770,1270,644			35,5996,17		0	461	2014	4588

ПОЛИГОН ЧАСТОТ

n 4

Рис.2.

1.3. Подсчитаем выборочные параметры по формулам:

= 1

= 191 =6,367

Выборочное среднее X ср

∑ хi ,

X ср

i=1

= 1

= 224,97 =7,499

Выборочную дисперсию DВ

∑(хi − Хср )2

DВ

i=1

Выборочное среднеквадратическое отклонение σ В =

DВ

, σ В = 2,738

− X ср )3 ,

62,058

=0,101

Выборочную симметрию AВ

∑(хi

AВ

nσ

i=1

30 * 2,738

4588

Выборочный эксцесс EВ

= −3 +

∑(хi − X ср )4 ,

EВ

- 3 = -0,28

nσ

i=1

30 * 2,738

Уточненную выборочную дисперсию D

= 30 7,499 =7,758

УТ

n − 1

Выборочный стандарт S =

DУТ

=2,785

Задание 2

Величины Хср, Dут, S случайные и являются точечными оценками математиче-

ского ожидания М[X] дисперсии D[X] и среднеквадратического отклонения

σ= D[ X ] наблюдаемой в выборке случайной величины Х.

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023378.47 Кб23637.pdf
#
21.11.2023378.5 Кб03638.pdf
#
21.11.2023378.51 Кб03639.pdf
#
21.11.2023112.02 Кб0364.pdf
#
21.11.2023378.65 Кб03640.pdf
#
21.11.2023378.73 Кб03641.pdf
#
21.11.2023378.76 Кб03642.pdf
#
21.11.2023378.8 Кб03643.pdf
#
21.11.2023379.13 Кб03644.pdf
#
21.11.2023379.17 Кб03645.pdf
#
21.11.2023379.23 Кб13646.pdf