
3430
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
О.Г. Антоновская, Н.Х. Селиванова
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Учебно-методическое пособие
по подготовке к практическим занятиям по дисциплине «Математика» для обучающихся по направлению подготовки 09.03.03 Прикладная информатика, профиль Прикладная информатика в юриспруденции
Нижний Новгород
2018
1
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Нижегородский государственный архитектурно-строительный университет»
О.Г. Антоновская, Н.Х. Селиванова
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Учебно-методическое пособие
по подготовке к практическим занятиям по дисциплине «Математика» для обучающихся по направлению подготовки 09.03.03 Прикладная информатика, профиль Прикладная информатика в юриспруденции
Нижний Новгород ННГАСУ
2018
2
УДК 517.9
Антоновская О.Г., Селиванова Н.Х. Кривые и поверхности второго порядка [Электронный ресурс]: учеб. - метод. пос. / О. Г. Антоновская, Н. Х. Селиванова; Нижегор. гос. архитектур. - строит. ун - т – Н. Новгород: ННГАСУ, 2018. – 43 с; ил. 1 электрон. опт. диск (CD-RW)
Приведены указания по подготовке к практическим занятиям по дисциплине «Математика». Приведены определения и классификация кривых и поверхностей второго порядка. Рассмотрены кривые в полярной системе координат и методы приведения уравнений кривых второго порядка к простейшему виду. Даны контрольные задания по теме «Кривые и поверхности второго порядка».
Предназначено обучающимся в ННГАСУ по направлению подготовки 09.03.03 Прикладная информатика, профиль Прикладная информатика в юриспруденции.
.
©О. Г. Антоновская, Н.Х. Селиванова, 2018
©ННГАСУ, 2018.
3
§ 1. Понятие кривой на плоскости
Пусть задана декартова прямоугольная система координат Oxy . Кривой (или линией) на плоскости называется множество точек плоскости, координаты которых удовлетворяют уравнению F (x, y) = 0 , где F (x, y)– некоторая функция двух переменных. Для того, чтобы множество точек, координаты которых являются решениями уравнения F (x, y) = 0 , соответствовало наглядному представлению о кривой, на функцию F (x, y) накладывают соответствующие ограничения. Например, множество точек плоскости, координаты которых удовлетворяют линейному уравнению Ax + By + C = 0 , есть прямая.
Знание уравнения линии позволяет для любой точки определить, принадлежит ли она линии. Если координаты точки удовлетворяют уравнению линии, то точка принадлежит этой линии, если не
удовлетворяют – не принадлежит. |
|
Пример. Определить, |
принадлежат ли точки M1 (− 1,3) и M 2 (1,1) |
линии, заданной уравнением |
y − x2 − x − 3 = 0 . |
Решение. При подстановке координат точек M1 и M 2 в уравнение получим 3 -1 +1 - 3 = 0 , 0 = 0 ; 1 -1 -1 - 3 = -4 , - 4 ¹ 0 . Следовательно, точка M1 принадлежит, а точка M 2 – не принадлежит данной линии.
Важный класс линий составляют те, для которых функция F (x, y) есть многочлен от двух переменных. В этом случае линия называется
алгебраической |
кривой, а степень многочлена |
– порядком |
кривой. |
|||
Алгебраическая |
кривая |
первого |
порядка |
– |
это прямая |
линия. |
Алгебраические |
кривые |
второго |
порядка – |
это |
окружность, |
эллипс, |
гипербола и парабола – будут изучаться в дальнейшем. |
|
|||||
Общее уравнение кривой второго порядка имеет вид: |
|
|||||
Ax2 |
+ 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0 , |
|
(1) |
|||
где хотя бы один из коэффициентов A, B,C не равен нулю.
§ 2. Окружность. Каноническое уравнение окружности
Окружностью называется множество, состоящее из всех точек плоскости (геометрическое место точек), находящихся на равном расстоянии R от фиксированной точки C . Число R называется радиусом окружности, а точка C – её центром.
Найдем уравнение окружности в заданной системе координат oxy . Пусть точка C совпадает с началом координат O(0,0), а M (x, y) – текущая точка окружности, т.е. точка, описывающая окружность.

4
y
M(x,y)
R
О x
Рис. 1.
Из определения окружности следует, что точка M (x, y) тогда и
только тогда принадлежит окружности, когда |
OM |
= R или |
x2 + y 2 |
= R , |
возводя обе части этого равенства в квадрат, получим уравнение |
|
|||
x2 + y 2 = R2 . |
(2) |
|||
Это есть каноническое уравнение окружности с центром в начале координат и радиусом R .
Если центр окружности находится в точке C(x0 , y0 ), то уравнение такой окружности будет
(x − x |
0 |
)2 |
+ (y − y |
0 |
)2 |
= R2 |
. |
(3) |
||
|
|
|
|
|
|
|
|
|||
Возводя двучлены, стоящие в левой части равенства (3), в квадрат, |
||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
x2 + y 2 − 2x |
x − 2 y |
0 |
y + x2 |
+ y2 |
− R2 = 0 . |
|||||
|
|
|
0 |
|
|
|
0 |
0 |
|
|
Мы видим, что уравнение окружности есть алгебраическое |
||||||||||
уравнение второй степени, и, |
сравнивая с уравнением (1), получаем, что |
|||||||||
уравнение (1) есть окружность, если B = 0 и A = C . Обратное тоже верно. |
||||||||||
Пример. Показать, что |
уравнение |
x2 |
+ y 2 |
− 8x + 2 y + 8 = 0 задает |
||||||
окружность. Найти ее центр и радиус.
Решение. Т.к. B = 0 , A = C = 1 – это окружность. Выделим полные квадраты
x2 − 8x + 16 − 16 + y 2 + 2 y + 1 − 1 + 8 = 0
(x − 4)2 − 16 + (y + 1)2 − 1 + 8 = 0
(x − 4)2 + (y + 1)2 = 9.
Получили уравнение окружности с центром в т.C(4,−1) и радиусом R = 3 .

5
§ 3. Эллипс. Каноническое уравнение эллипса
Эллипсом называется множество, состоящее из точек плоскости, сумма расстояний от которых до двух фиксированных точек F1 и F2 , называемых фокусами, есть величина постоянная, большая, чем
расстояние между фокусами. |
|
||||||||||||||
Пусть 2c – расстояние между фокусами, 2a |
– постоянная сумма |
||||||||||||||
расстояний. В силу определения a > c > 0 . Точка М – |
произвольная точка |
||||||||||||||
эллипса, тогда |
|
||||||||||||||
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
= 2a . |
(4) |
|
|
|
|
|
F1M |
|
|
F2 M |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторы F1M и F2 M , а так же их модули называют фокальными радиусами.
y
|
|
M(x,y) |
|
F1 |
|
F2 |
|
-с |
0 |
с |
x |
Рис. 2.
Выведем уравнение эллипса в специально выбранной системе
координат, где ось абсцисс проходит через точки F1 и F2 , |
начало |
||||
координат делит отрезок F1 F2 пополам, и система координат oxy – |
правая. |
||||
В выбранной системе координат уравнение (4) имеет вид |
|
||||
|
|
+ |
|
= 2a . |
|
|
(x + c)2 + y 2 |
(x − c)2 + y 2 |
(5) |
||
Это и есть уравнение эллипса. Приведем его к более простому виду путем возведения в квадрат и введения новой величины
b2 = a 2 − c2 > 0 , |
(6) |
||||
а именно |
|
|
|
|
|
|
x2 |
+ |
y 2 |
= 1. |
(7) |
|
a2 |
b2 |
|||
|
|
|
|
||
Уравнение (7) называется каноническим уравнением эллипса.
Основные характеристики эллипса:
1.Оси ox и oy – оси симметрии, начало координат – центр симметрии эллипса.
2.Эллипс целиком расположен внутри прямоугольника: x ≤ a , y ≤ b .
3.Точки A1 (− a,0), A2 (a,0), B1 (0,−b), B2 (0,b) – вершины эллипса.

|
|
|
|
|
6 |
|
|
|
|
|
4. |
a – |
большая полуось, b – |
малая |
полуось |
(a > b) и |
c = |
b2 − a2 |
– |
||
|
полуфокусное расстояние. |
|
|
|
|
|
|
|||
5. |
Эксцентриситет |
эллипса |
– |
это |
ε = c < 1. |
|
Отношение |
|||
|
|
a2 − c2 |
|
|
|
|
a |
|
|
|
|
b = |
= |
1 − ε 2 . Отсюда видно, что чем ближе ε |
к единице, |
||||||
|
a |
a |
|
|
|
|
|
|
|
|
|
тем меньше b , т.е. эллипс более вытянут. Если эксцентриситет близок к |
|||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
нулю, эллипс по форме близок к окружности. Случай, когда ε = 0, т.е. |
|||||||||
|
a = b – есть окружность. |
|
|
|
|
|
|
|||
6. |
Директрисы эллипса: x = ± a . |
|
|
|
|
|
|
|||
|
|
|
|
ε |
|
|
|
|
|
|
7. |
Фокальные радиусы т. M (x, y) эллипса: |
|
|
|
|
|||||
|
|
|
|
F1M = a + εx |
|
|
|
|
||
|
|
|
|
F2 M = a − εx . |
|
|
|
|
||
|
|
|
|
|
y |
|
|
|
|
|
|
x = − a |
|
|
|
|
|
|
x = a |
||
|
|
ε |
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
B2(0,b) |
|
|
|
|
|
|
|
|
|
|
|
M(x,y) |
|
|
|
|
|
A1(-a,0) |
|
|
|
|
A2(a,0) |
|
||
|
|
|
|
F1(-c,0) |
0 |
|
F2(c,0) |
|
x |
|
|
|
|
|
|
|
B1(0,-b) |
|
|
|
|
|
Рис. 3. |
|
|
|
|
|
|
|
|
|

|
|
|
|
|
7 |
|
«Вырождения» эллипса: |
||||||
1. |
x2 |
+ |
y 2 |
= 0 – |
задает точку O(0,0); |
|
a2 |
b2 |
|||||
|
|
|
|
|||
2. |
x2 |
+ |
y 2 |
= −1 – |
мнимый эллипс. |
|
a2 |
b2 |
|||||
|
|
|
|
|||
Пример. Составить каноническое уравнение эллипса, проходящего через точки M1 (
 2, 2
2, 2
 2 ) и M 2 (1, 2
2 ) и M 2 (1, 2
 3). Построить кривую.
3). Построить кривую.
|
|
Решение. Каноническое уравнение эллипса имеет вид |
|
x2 |
|
|
+ |
y 2 |
|
= 1. |
|||||||||||||||||||||
|
|
a2 |
|
|
b2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если точки M1 и M 2 лежат на эллипсе, то их координаты удовлетворяют |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
уравнению кривой, т.е. |
|
|
+ |
|
|
|
= 1 |
|
|
|
|
||||||||||||||||||||
a2 |
b2 |
. Решая эту систему, относительно a2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
и |
b2 , найдем |
b2 = 16, a2 |
= 4 . |
|
|
|
Уравнение |
|
эллипса |
x2 |
+ |
y 2 |
|
= 1. |
|
Т.к. |
|||||||||||||||
|
4 |
16 |
|
||||||||||||||||||||||||||||
a = 2 < b = 4 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
то |
фокусы |
этого |
эллипса |
находятся |
на |
оси |
|
oy |
и |
||||||||||||||||||||||
c = |
|
|
= 2 |
|
|
. Итак, F1 (0,−2 |
|
|
) и F2 (0, 2 |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
16 − 4 |
|
3 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y
4
2
 3 F2
3 F2
-2 |
0 |
2 |
x |
− 2
 3 F1
3 F1
-4
Рис. 4.

8
§ 4. Гипербола. Каноническое уравнение гиперболы
Гиперболой называется множество, состоящее из всех точек плоскости, абсолютная величина разности расстояний от которых до двух фиксированных точек F1 и F2 , называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами, и отличная от нуля.
Пусть 2c – расстояние между фокусами F1 и F2 , 2a – постоянная абсолютная величина разности расстояний. В силу определения c > a > 0 . Пусть M – произвольная точка гиперболы, тогда
F1 M |
|
− |
|
F2 M |
|
= 2a . |
(8) |
|
|
|
|||||
|
|
|
Векторы F1M и F2 M , а так же их модули называют фокальными радиусами гиперболы. Выведем уравнение гиперболы в специально выбранной системе координат.
y
M(x,y)
F1(-c,0) |
0 |
F2(с,0) |
x |
|
|
Рис. 5.
Пусть точка M (x, y) – произвольная точка гиперболы, тогда для нее выполняется равенство (8).
|
− |
|
|
= 2a . |
|
(x + c)2 + y 2 |
(x − c)2 + y 2 |
|
(9) |
Это и есть уравнение гиперболы в выбранной системе координат. Преобразуем (9) к более простому виду, дважды возведя в квадрат и упрощая, получим
|
x2 |
|
− |
|
y 2 |
= 1. |
||
|
a2 |
c2 − a2 |
||||||
|
|
|
|
|||||
Введем новую величину b2 = c2 |
|
− a 2 > 0 , тогда |
||||||
|
|
x2 |
|
− |
y 2 |
= 1. |
(10) |
|
|
|
a2 |
|
|
||||
|
|
|
|
|
b2 |
|
||
Уравнение (10) называется каноническим уравнением гиперболы.
9
Основные характеристики гиперболы:
1.Оси ox и oy – оси симметрии гиперболы, начало координат – центр симметрии гиперболы.
2.Область расположения гиперболы x ³ a , с осью oy гипербола не пересекается. Точки A1 (− a,0), A2 (a,0) называются вершинами гиперболы. Действительной осью называется ось, пересекающаяся с кривой (в уравнении (10) ось ox ), а мнимой – ось, не пересекающаяся с кривой ( oy ).
3.а – действительная полуось, b – мнимая полуось, c = 
 a 2 + b2 – полу фокусное расстояние.
a 2 + b2 – полу фокусное расстояние.
|
Эксцентриситет гиперболы - это ε = |
c |
> 1, |
b |
= |
|
|
c2 − a2 |
= |
|
|
. |
||||
4. |
|
|
|
ε 2 −1 |
||||||||||||
|
|
|
|
a |
||||||||||||
|
|
|
|
|
|
a |
a |
|
|
|
|
|
|
|||
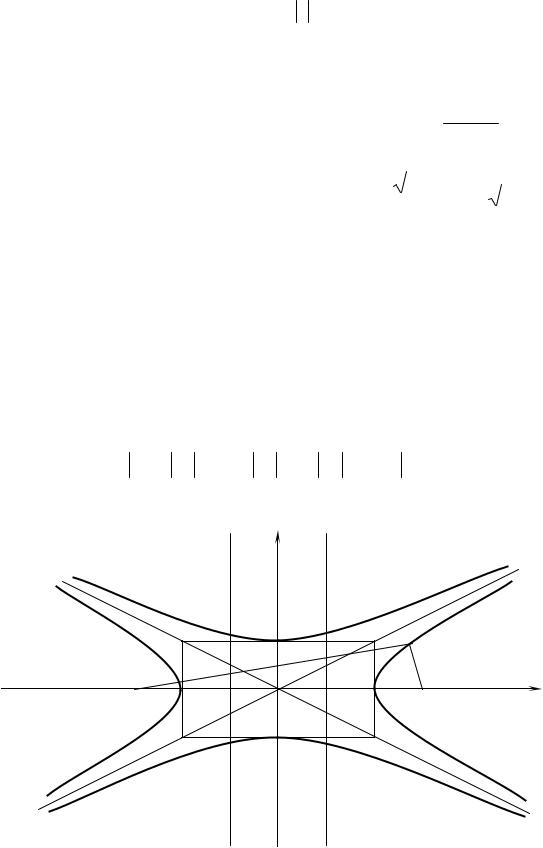
5. |
Асимптоты гиперболы: y = ± |
b |
x . Асимптоты являются диагоналями |
|||||||||||||
|
|
|||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|||||
|
прямоугольника со сторонами x = ±a, y = ±b . |
Этот прямоугольник |
||||||||||||||
|
называют основным прямоугольником гиперболы. Вся кривая |
|||||||||||||||
|
расположена вне прямоугольника, и только вершины A1 , |
A2 |
лежат на |
|||||||||||||
|
сторонах x = ± a . |
|
|
|
|
|
|
|
|
|
||||||
6. |
Директрисы гиперболы: x = ± |
a |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ε |
|
|
|
|
|
|
|
|
|
||||
7. |
Фокальные радиусы т. M (x, y) гиперболы: |
|
|
|
|
|
|
|
|
|
||||||
F1 M = ε x + a u F2 M = ε x − a .
y
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
M(x,y) |
|
F1(-c,0) |
-a |
0 |
a |
F2(c,0) |
x |
||
|
|
|
-b |
|
|
|
|
|
x = − |
a |
|
x = |
a |
|
|
|
ε |
|
|
|
|||
|
|
ε |
|
|
|||
Рис. 6.
