
3179
.pdf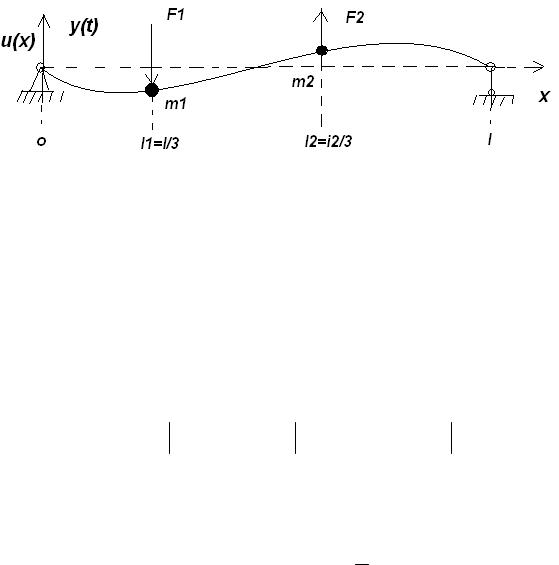
|
|
|
с |
= α |
|
c . Коэффи- |
||||||||
может быть найдена из уравнения статического равновесия |
X |
F |
||||||||||||
циент влияния α |
кi |
= X с (F c ) |
будет равен статическому перемещению по x |
к |
от |
|||||||||
|
|
|
к |
i1 |
|
|
|
|
|
|
|
|
||
единичной |
внешней |
силы, |
действующей только |
|
по |
координате |
xi |
|||||||
F с |
= (0,0 ,.. |
,1 = F ,0,.. 0) . |
|
|
|
|
|
|
|
|
|
|||
i1 |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
Пример [2]. |
Рассмотрим малые поперечные колебания двух точечных масс |
||||||||||||
m1., |
m2 прикрепленных к шарнирно опертой балке длины l |
на расстояниях l / 3 |
от |
|||||||||||
опертых концов. Пусть балка невесома, совершает изгибные колебания и описыва-
ется моделью Бернулли с жесткостью EJ .
Координаты системы y1 (t), y2 (t) задают малые поперечные смещение точечных
масс, Смещения срединной линии балки u(x) для невесомой балки определяются по координатам масс из следующей краевой задачи
|
|
|
|
|
|
EJu xxxx = 0, |
|
|
|
|
|
||||
u |
|
x=0 = 0, |
EJuxx |
|
x=0 = 0, |
u |
|
x=l = 0, |
EJuxx |
|
x=l = 0, |
||||
|
|
|
|
||||||||||||
|
|
|
= y1 , |
[u x ] |
|
= 0, [EJu xx |
] |
|
x=l = 0, |
||||||
|
|
u |
x=l |
x=l |
|
||||||||||
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|||
u x=l2 = y2 , [u x ] x=l2 = 0, [EJ × u xx ] x=l2
= 0,
Решение для изогнутой оси балки зависит от 12-ти констант, определяемых из краевых условий, и позволяет вычислить потенциальную энергию упругой балки
l
1
П( y1 , y2 ) = ∫0 2EJuxx2 dx .
Однако проще определить коэффициенты влияния, используя известное статическое решение [4] для изогнутой оси балки от действия постоянной поперечной си-
лы Р0 в точке приложения ξ
10
|
|
u(x,ξ ) = |
P0 x(l − ξ ) |
(l 2 − x 2 − (l − ξ )2 ) , |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6lEJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из которого, при P0 |
= 1 и l1 |
|
= l / 3, |
l2 = 2l / 3 получим при различных значе- |
||||||||||||||||||||||||||||||||
ниях x и ξ : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α11 = u(x = l1 ,ξ = l1 ) = |
|
4 |
|
|
l 3 |
|
, α12 = u(x = l1 |
,ξ = l2 ) = |
|
|
7 |
|
|
l 3 |
|
|
|
|||||||||||||||||||
|
243 EJ |
|
|
486 EJ |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
α 21 = u(x = l21 ,ξ = l1 ) = |
|
7 |
|
|
|
|
l 3 |
, α 22 = u(x = l |
2 ,ξ = l2 ) = |
4 |
|
|
|
l 3 |
|
|
. |
|||||||||||||||||||
486 EJ |
243 EJ |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Таким образом матрицы влияния и жесткости будут следующими |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
α = |
1 |
|
|
l |
3 |
|
|
8 |
7 |
|
|
С = α |
−1 |
= |
486 EJ |
|
|
8 |
|
|
− 7 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
− 7 |
|
|
|
. |
|||||||||||
|
|
|
|
|
|
7 |
8 |
|
15 l |
3 |
8 |
|||||||||||||||||||||||||
|
486 EJ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Кинетическая энергия системы и матрица инерции легко определяется
|
|
1 |
|
|
2 |
m |
|
& |
& |
& 2 |
& |
|
1 |
||
|
2 ) , |
|
|||||
Т( y1 |
, y2 ) = |
2 |
( y1 |
+ y |
M = |
0 |
|
|
|
|
|
|
|
||
0
m2 .
Если трением в системе можно пренебречь, то матрица диссипации D=0, а динамические уравнения системы будут следующими:
m1 &y&1 + c11 y1 + c12 y2 = F1
m2 &y&2 + c21 y1 + c22 y2 = F2 .
11

1.3. РЕШЕНИЕ И АНАЛИЗ УРАВНЕНИЙ ДИНАМИКИ СИСТЕМЫ
Решение уравнений динамики системы (1) с начальными условиями (2) в математике решается различными методами, например операционным методом интегральных преобразований Лапласа [3] оно сводится к линейной неоднородной системе алгебраических уравнений
( |
( |
|
|
|
|
||
(Mp 2 + Dp + C) |
|
= |
|
+ pX |
|
+ V |
|
X |
F |
0 |
, (3) |
||||
|
|
|
|
|
0 |
||
|
|
|
( |
∞ |
|
|
|
|||||
|
|
|
|
|
( p) = ∫ |
|
(t) × e− pt dt |
|
|
|
||
|
|
|
X |
X |
изображение искомой функции |
|
(t) , |
|||||
где |
|
X |
||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
а p = s + iσ комплексная переменная. |
|||
|
|
( p) изображение заданных сил |
|
(t) , |
||||||||
|
F |
F |
||||||||||
Решение уравнения (3) легко находится по правилу Крамера[5], в виде правильной
|
( |
|
|
|
|
|
|
|
||
|
|
D |
2n−1 ( p) |
|
|
|||||
|
|
|
|
|
|
|||||
дроби |
X ( p) = |
, где |
2n ( p) = det(Mp 2 + Dp + C) главный опреде- |
|||||||
D |
2n ( p) |
|||||||||
|
|
|
|
|
|
|||||
литель, представляющий собой многочлен степени 2n, а 2n−1 ( p) вектор вспомо-
гательных определителей многочленов степени 2n-1. Обращение такой дроби в соответствии с теоремами разложения может быть проведено путем разложения его на сумму простейших дробей, имеющие табличное обращение.
Однако, для целей физического анализа решения, более подходящим является метод собственных чисел и собственных функций системы. В соответствии с ним, согласно общей теории дифференциальных уравнений общее решение уравнения (1) имеет следующую структуру:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
||
|
|
|
|
(t) = |
|
собств (t) + |
|
вынужд (t) , а |
|
собств (t) = ∑Ск |
|
кб (t) , |
|
||||||
|
|
|
|
|
|
Х |
Х |
|
|||||||||||
Х |
Х |
X |
(4) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к=1 |
|
||
где |
|
собств (t) общее решение |
|
|
|
|
|
||||||||||||
Х |
соответствующей однородной системы уравнений |
||||||||||||||||||
|
|
|
(t) = 0 , |
|
|
кб (t) линейно-независимая система |
|||||||||||||
(1) с нулевой правой частью, т.е. |
F |
Х |
|||||||||||||||||
базисных решений однородных |
уравнений |
(1), а Ск произвольные |
константы, |
||||||||||||||||
определяемые в дальнейшем из начальных условий (2). Поскольку однородные уравнения соответствуют отсутствию внешних сил, приложенных к механической
12
системе, то эта часть решения называется собственным (свободным) движением механической системы.
Другая часть общего решения X вынужд (t) представляет собой частное реше-
ние неоднородных уравнений (1) и называется вынужденным решением, так как обусловлена исключительно действием заданных внешних сил F (t) ¹ 0 .
Будем искать систему собственных базисных решений однородных уравнений (1) в виде
Хкб (t) = L × eλt ,
где λ произвольная константа и произвольный вектор констант L = (l j ) , которые
будем подбирать так, чтобы это решение удовлетворяло однородным уравнениям (1), подставляя его в уравнение, получаем:
(Mλ2 + Dλ + C) × L = 0 . (5)
Ненулевое решение этого однородного уравнения возможно лишь при условии того что λ является корнями следующего характеристического уравнения:
2n (λ) = det(Mλ2 + Dλ + C) = 0 . |
(6) |
Это алгебраическое уравнение порядка 2n по основной теореме алгебры оно имеет 2n корней с учетом их кратности. причем в силу симметричности характеристиче-
ской матрицы А = Mλ2 + Dλ + C и вещественности коэффициентов уравнения
(6) его корни будут попарно комплексно-сопряженными λк = -δ к ± iωк к =1,2, …., n и называются собственными числами механической системы. Константы
δ к ³ 0 называются коэффициентами затухания, так как δ к = 0 при отсутствии диссипации D = 0 и δ к > 0 при наличии диссипации, а константы ωк ³ 0 назы-
ваются собственными частотами системы, причем собственные частоты пронумеро-
ваны по возрастанию 0 £ ω1 £ ω2 £ ω3 £ .... £ ωn , ω1 - первая (низшая, ос-
новная) частота.
13

Каждой паре собственных чисел λк соответствует решение уравнения (5)
Lк = (lкj ) , называемое собственными векторами системы, причем, поскольку ре-
шение уравнения (5) представляется однопараметрическим множеством, то одну из компонент вектора Lк = (lкj ) можно задать произвольной константой, например
(lк1 = 1) . Если собственное число кратно, то имеется многопараметрическое мно-
жество решений и произвольными константами можно задавать количество компонент равное кратности.
Определив все собственные числа и вектора системы, можем найти систему линейно-независимых базисных решений Хкб (t) = Lк × eλt однородного уравнения
(1) и построить общее решение для собственных движений механической системы .
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
собств (t) = ∑ |
|
|
к × (С2к−1e−δ к +iωк |
+ С2кe−δ к −iωк ) = |
|
||||||||||||||
Х |
L |
|
||||||||||||||||||||
|
|
|
|
к=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= ∑ |
|
к × е−δ к × (С2к−1 Sinωкt + С2кCosωкt) = |
|
|
|
|
||||||||||||||||
L |
|
|
|
(7) |
||||||||||||||||||
к=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∑ |
|
к × Aк е |
−δ кt × Sin(ωкt + aк ) , |
|
|
|
|
|||||||||||
|
|
|
|
L |
|
|
|
|
||||||||||||||
|
|
|
|
к=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Где С2к−1 , C2к или Ак , ак пары произвольных констант, причем связанные из- |
||||||||||||||||||||||
вестными соотношениями для гармонических функций: |
|
|
|
|
||||||||||||||||||
|
|
|
С2 |
+ C 2 |
= А2 , |
|
|
|
С2к |
= tg(aк ) . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2к−1 |
2к |
|
|
|
|
|
к |
|
|
С2к−1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
б (t) = |
|
|
× A e |
−δt Sin(ω |
t + a |
|
) |
|
|||||||||
Базисные функции в виде |
|
|
Х |
L |
к |
к |
называются |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
к |
к |
|
|
|
|||
собственными формами колебаний механической системы. Как видно из приведенного решения, собственные движения механической системы носят колебательный характер и представляются по каждой координате суммой собственных форм коле-
баний с амплитудой Ак на собственных частотах ωк и с начальными фазами ак .
Суммарное собственное движение представляется в зависимости от соотношения частот, амплитуд и фаз собственных форм колебаний хаотическим, почти
14
«случайным» движением, однако в частности, подобрав соответствующие начальные условия можно возбудить только одну из собственных форм и наглядно увидеть ее. С другой стороны оказывается, что линейным преобразованием с матрицей
перехода L = (Lк ) = (lкj ) можно подобрать новые координаты системы
Z (t) = L × X (t) такие что, матрицы жесткости, инерции и диссипации будут иметь диагональный вид. Тогда уравнения (1) расщепляются и становятся независимыми по каждой из новых координат
mк &z&к + d к z&к + ск zк = Fк (t) ,
Такие координаты называются главными, и их изменение происходит в соответствии с законами движения линейного гармонического осциллятора.
Вынужденные движения совершаются при наличии внешних сил,
приложенных к системе и могут быть найдены различными математическими методами такими как метод вариации произвольных постоянных, операционный метод, методы Дюамеля и Грина [3], Но наше решение будет проще, - зададимся гармоническим видом переменных внешних сил
F (t) = f × Sin(Wt + ϕ) = Im[ f × ei(Ωt +ϕ ) ] ,
где f = ( fк ) вектор амплитуд внешних сил изменяющихся с одной частотой Ω и
с одной начальной фазой ϕ . Будем искать вынужденное движение так же в гармо-
ническом виде:
X вынужд (t) = B × Sin(Wt + b) = Im[B × ei (Ωt +b) ] , (8)
где неизвестный вектор амплитуд вынужденных колебаний, возбуждае-
мых на частоте внешней силы и с неизвестной начальной фазой b. Выражения в квадратных скобках представляют собой комплексную внешнюю силу и комплексное решение соответственно
|
~ |
|
|
|
|
~ |
|
|
|
F (t) = f × ei (Ωt +ϕ ) |
X вынужд (t) = B × ei (Ωt +b) . |
||||||||
Подставляя в (1) мнимую часть комплексного решения получим, что амплитуда и фаза вынужденных колебаний удовлетворяют уравнению
15

(М(iW)2 + D(iW) + C) |
|
= |
fei(ϕ −b) |
|
|
|
|
|
||||
B |
разделяя действительную и мнимые части |
|||||||||||
получим два уравнения |
|
|
|
|
|
|||||||
(-МW2 + C) |
|
|
|
|
|
|
|
|
|
|||
B |
= f |
× Cos(ϕ - b) , |
DW |
B |
= f × Sin(ϕ - b) (9) |
|||||||
из которых могут быть найдены амплитуды Bк = Bк (W) и фаза b = b(Ω) вынуж- |
||||||||||||
денных колебаний как функции частоты внешней гармонической силы. Эти функции называются амплитудно-частотными (АЧХ) и фазо-частотными (ФЧХ) характеристиками динамического поведения механической системы. Физический смысл АЧХ и ФЧХ состоит в том, что они показывают как система откликается на переменное внешнее воздействие в форме вынужденных колебаний. АЧХ является одновременно и коэффициентом динамичности механической системы.
В частности при отсутствии диссипации D = 0 смещение фаз вынужденных колебаний и вынуждающей силы отсутствуетϕ = b , тогда из (9) по правилу Краме-
ра находим АЧХ
|
2 |
|
−1 |
|
|
|
Dк2n−2 (W) |
|
Bк (W) = (-МW |
+ C) |
× f = |
||||||
|
|
D2n (W) |
||||||
|
|
|
|
|
|
|
||
При близости частоты внешней силы хотя бы к одной из собственных частот глав-
ный определитель D2n (W » ωк ) » 0 близок нулю и в системе имеет место резо-
нансное усилении колебаний. Частоты внешней силы W*r » ωк называются резо-
нансными. Типичный вид АЧХ приводится.
16
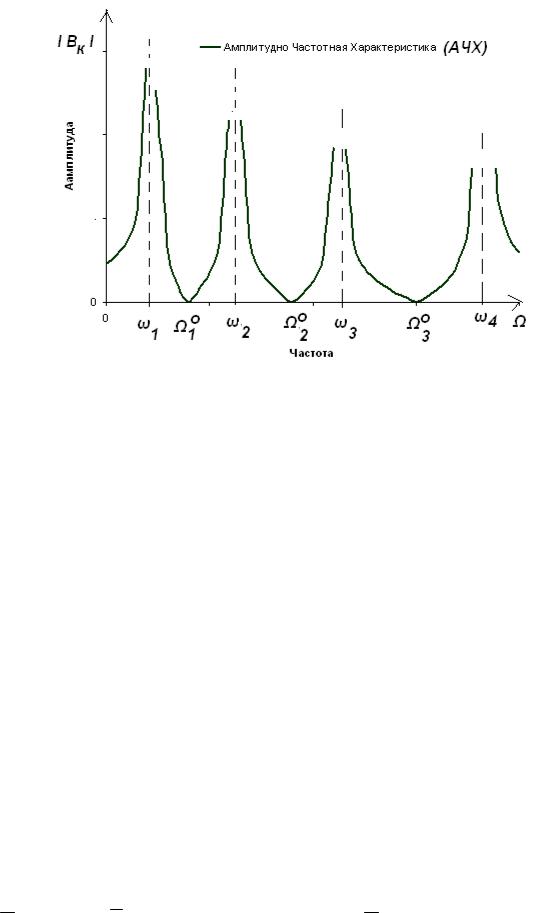
Видим, что существуют частоты внешней силы W0к , называемые антирезонансны-
ми , при которых вынужденные колебания не возбуждаются, т.е. система не реагирует на переменное внешнее воздействие. Если антирезонансные частоты существуют, то они находятся из находятся нулю вспомогательных определителей Кра-
мера Dк2т−2 (W0к ) = 0 .
При наличии диссипации в системе решения уравнений (9) неограниченных амплитуд уже не дают, но частоты внешних сил при которых наблюдаются максимальные и минимальные амплитуды остаются присутствовать в линейке собственных частот системы а потому так же называются квазирезонансными и квазиантирезонасными частотами соответственно.
Зная амплитудно-частотную характеристику механической системы, моделирующей некоторую, например, строительную конструкцию, можно при проектировании конструкции размещать ее собственные частоты вдали от частот внешних воздействий, а антирезонансные наоборот ближе к ним.
В заключении напомним, что общее решение уравнений (1) согласно (4):
т
Х(t) = = ∑ Lк × Aке−δ кt × Sin(ωкt + aк ) + B × Sin(Wt + b)
к=1
Вкотором константы Ак , ак определяются из начальных условий (2).
17
2. ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИ РАСЧЕТНО -ГРАФИЧЕСКОЙ РАБОТЫ
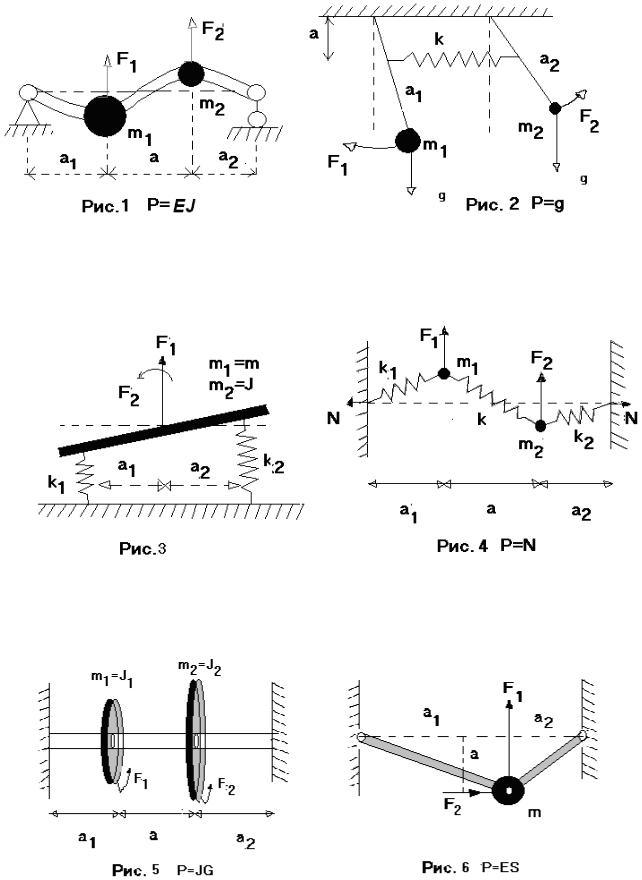
Для упругих механических систем с двумя степенями свободы, изображенных ниже на рисунках и с параметрами, приведенными в таблице, где n – последняя цифра номера учебной группы, выполнить следующие задания:
1) Ввести координаты состояния х1 (t), х2 (t) и составить уравнения динами-
ческой модели 4-го порядка для описания движений системы.
2) |
Найти собственные частотыω1 ,ω2 |
(ω1 < ω2 ) и |
собственные вектора |
|||||||||||||||||||
|
|
|
|
|
|
Определить собственные формы Х1б , Х2б |
|
|
|
|
||||||||||||
L1 , L2 . |
|
|
колебаний упругой системы. |
|
||||||||||||||||||
3) |
Построить |
Амплитудно-частотные характеристики для вынужденных колебаний по |
||||||||||||||||||||
каждой |
из координат системы при |
|
действие |
на |
нее |
внешних |
гармонических |
сил |
||||||||||||||
F1 = f1CosΩt |
и |
F2 = f2CosΩt |
в диапазоне изменения частоты внешних сил |
|||||||||||||||||||
0 < Ω < 1.2ω2 . Определить резонансные |
Ω1* , Ω*2 |
и антирезонансные Ω10 , Ω02 частоты |
||||||||||||||||||||
системы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4) Для частоты внешней силы |
Ω |
|
= |
1 |
(ω + ω |
|
) |
найти амплитуды В1 , В2 |
вы- |
|||||||||||||
0 |
|
2 |
||||||||||||||||||||
|
2 |
1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нужденных колебаний, |
найти |
амплитуды |
А1 , А2 |
|
и начальные фазы ϕ1 ,ϕ2 соб- |
|||||||||||||||||
ственных форм колебаний. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
построить полное |
решение |
при заданных начальных |
условиях для координат |
|||||||||||||||
х (t), х (t) и построить их графики |
в диапазоне времени |
0 ≤ t ≤ 2 |
2π |
|
|
|||||||||||||||||
ω1 |
|
|||||||||||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
18
19
